Pengaturcaraan linear Apa itu, model, sekatan, aplikasi

The pengaturcaraan linear Ia adalah kaedah matematik yang berfungsi untuk mengoptimumkan (memaksimumkan atau meminimumkan seperti yang diperlukan) fungsi yang pembolehubahnya tertakluk kepada sekatan, selagi fungsi dan sekatan bergantung kepada pembolehubah.

Umumnya fungsi untuk mengoptimumkan keadaan praktikal, seperti keuntungan pengeluar yang input, buruh atau jentera adalah terhad.

Rajah 1. Pengaturcaraan linear digunakan secara meluas untuk mengoptimumkan keuntungan. Sumber: PIQSELS.

Salah satu kes yang paling mudah ialah fungsi linear untuk memaksimumkan, yang hanya bergantung kepada dua pembolehubah, yang dipanggil Pembolehubah keputusan. Ia boleh menjadi bentuk:

Z = k₁x + k₂dan

Dengan k₁ dan k₂ pemalar. Fungsi ini dikenali sebagai Fungsi objektif. Sudah tentu terdapat situasi yang merit lebih daripada dua pembolehubah untuk kajian mereka, menjadi lebih kompleks:

Z = k₁x₁ + k₂x₂ + k₃x₃ +… .

Dan sekatan juga dimodelkan secara matematik melalui sistem persamaan atau kekurangan, sama linear dalam x dan dan.

Set penyelesaian sistem ini dipanggil penyelesaian yang boleh dilaksanakan Sama ada mata yang boleh dilaksanakan. Dan di antara titik -titik yang boleh dilaksanakan ada sekurang -kurangnya satu, yang mengoptimumkan fungsi objektif.

Pengaturcaraan linear dibangunkan secara bebas oleh ahli fizik dan ahli matematik Amerika.

Kaedah penyelesaian masalah yang dikenali sebagai Kaedah simplex Ia adalah penciptaan Dantzig, yang bekerja untuk Tentera Udara AS, Universiti Berkeley dan Stanford University.

Rajah 2. Ahli matematik George Dantzig (kiri) dan Leonid Kantorovich (kanan). Sumber: f. Zapata.

[TOC]

Model pengaturcaraan linear

Unsur -unsur yang diperlukan untuk menubuhkan model pengaturcaraan linear, sesuai dengan situasi praktikal, adalah:

-Fungsi objektif

-Pembolehubah keputusan

-Sekatan

Dalam fungsi objektif, apa yang ingin anda capai ditakrifkan. Sebagai contoh, katakan ia dikehendaki untuk memaksimumkan keuntungan yang diperoleh daripada pembuatan produk tertentu. Kemudian fungsi "keuntungan" ditubuhkan, mengikut harga di mana produk dijual.

Dalam istilah matematik, fungsi ini boleh dinyatakan disingkat menggunakan penjumlahan:

Z = Σk_Yo x_Yo

Dalam persamaan ini, k_Yo Mereka adalah pekali dan x_Yo adalah pembolehubah keputusan.

Pemboleh ubah keputusan adalah unsur -unsur sistem yang kawalannya dan nilai mereka adalah nombor sebenar positif. Dalam contoh yang dicadangkan, pembolehubah keputusan adalah jumlah setiap produk yang akan dihasilkan untuk mendapatkan keuntungan maksimum.

Akhirnya, kita mempunyai sekatan, yang merupakan persamaan linear atau ketidaksamaan dari segi pembolehubah keputusan. Mereka menggambarkan batasan masalah, yang diketahui dan boleh menjadi contoh jumlah bahan mentah yang terdapat dalam pembuatan.

Boleh melayani anda: fungsi lebih tinggi daripada dua (contoh)

Jenis sekatan

Anda boleh mempunyai jumlah batasan, bermula dari J = 1 sehingga J = m. Secara matematik sekatan adalah tiga jenis:

1. Ke_J = Σ a_IJ . x_Yo
2. B_J ≥ Σ b_IJ . x_Yo
3. C_J ≤ Σ c_IJ . x_Yo

Sekatan pertama adalah jenis persamaan linear dan bermaksud bahawa nilai untuk_J, yang diketahui, harus dihormati.

Baki dua sekatan adalah kekurangan linear dan bermakna nilai b_J dan c_J, diketahui, boleh dihormati atau diatasi, apabila simbol yang muncul adalah ≥ (lebih besar atau sama dengan) atau menghormati atau tidak diatasi, jika simbol adalah ≤ (kurang dari atau sama dengan).

Contoh model

Bidang aplikasi sangat pelbagai, yang meliputi dari pentadbiran perniagaan ke pemakanan, tetapi untuk memahami kaedah, model mudah situasi praktikal dengan dua pembolehubah kemudian dicadangkan.

Pastri tempatan terkenal dengan dua kepakaran: Kek Jungle Hitam dan Kek Sacrista.

Dalam penjelasannya, mereka memerlukan telur dan gula. Untuk hutan hitam, 9 telur dan 500 g gula diperlukan, manakala 8 telur dan 800 g gula diperlukan untuk sacripenin. Harga jualan masing -masing adalah $ 8 dan 10.

Masalahnya ialah: Berapa banyak kek dari setiap jenis yang perlu dibuat pastri untuk memaksimumkan keuntungannya, mengetahui bahawa ia mempunyai 10 kilogram gula dan 144 telur?

Pembolehubah keputusan

Pembolehubah keputusan adalah "x" dan "y", yang mengambil nilai sebenar:

-X: Jumlah kek hutan hitam

-Y: kek jenis sacriphantine.

Sekatan

Sekatan diberikan oleh hakikat bahawa bilangan kek adalah jumlah yang positif dan terdapat jumlah bahan mentah yang terhad untuk mempersiapkannya.

Oleh itu, secara matematik, sekatan ini memperoleh bentuk:

1. x ≥ 0
2. dan ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 dan ≤ 10

Sekatan 1 dan 2 merupakan Keadaan bukan negativiti terdahulu terdedah, dan semua kekurangan yang dibangkitkan adalah linear. Dalam Sekatan 3 dan 4 adalah nilai yang tidak boleh diatasi: 144 telur dan 10 kg gula.

Fungsi objektif

Akhir. Ia dibina mengalikan harga dengan jumlah kek yang dibuat dan menambah untuk setiap jenis. Ini adalah fungsi linear yang akan kita panggil g (x, y):

G = 8x + 10y

Kaedah penyelesaian

Antara pelbagai metodologi penyelesaian adalah kaedah grafik, algoritma simplex dan kaedah titik dalaman, untuk menyebutkan beberapa.

- Kaedah grafik atau geometri

Apabila anda mempunyai masalah dua pembolehubah seperti bahagian sebelumnya, sekatan menentukan rantau poligonal dalam pesawat Xy, Panggilan Wilayah yang boleh dilaksanakan Sama ada Rantau daya maju.

Rajah 3. Rantau yang layak, di mana penyelesaian masalah pengoptimuman terletak. Sumber: Wikimedia Commons.

Rantau ini dibina melalui Garis sekatan, yang merupakan garis yang diperolehi dari kekurangan sekatan, hanya berfungsi dengan tanda kesamaan.

Boleh melayani anda: set terhingga: sifat, contoh, latihan yang diselesaikan

Dalam kes kedai roti yang ingin mengoptimumkan keuntungan, garis sekatan adalah:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Semua titik di rantau yang dikunci oleh garis -garis ini adalah penyelesaian yang mungkin, jadi ada yang tidak terhingga. Kecuali dalam kes di mana rantau yang layak kosong, di mana masalah yang dibangkitkan tidak mempunyai penyelesaian.

Nasib baik, untuk masalah pastri rantau yang boleh dilaksanakan tidak kosong, kita ada di bawah.

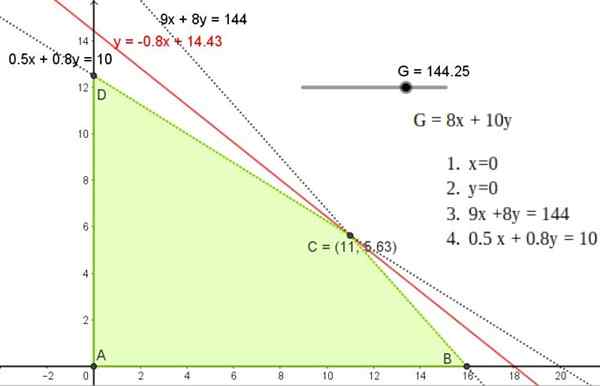
Rajah 4. Rantau masalah pastri yang boleh dilaksanakan. Garis lurus 0 melintasi asal. Sumber: f. Zapata dengan geogebra.

Penyelesaian yang optimum, jika ada, adalah dengan bantuan fungsi objektif. Contohnya, ketika mencari keuntungan m maksimum, anda mempunyai baris berikut, yang dipanggil ISO-Benefice Straight:

G = k₁x + k₂dan → y = -k₁x / k₂ + G/ k₂

Dengan garis ini semua pasangan (x, y) diperolehi yang memberikan keuntungan yang diberikan, jadi ada keluarga garis mengikut nilai g, tetapi semua dengan cerun yang sama -K₁ / k₂, Jadi mereka selari lurus.

Penyelesaian optimum

Sekarang, dapat ditunjukkan bahawa penyelesaian optimum masalah linear selalu menjadi melampau atau puncak dari kawasan yang layak. Jadi:

Penyelesaian garis adalah yang paling jauh dari asal dan yang mempunyai sekurang -kurangnya satu titik yang sama dengan kawasan yang layak.

Sekiranya garis yang paling dekat dengan asal mempunyai segmen keseluruhan yang sama dengan rantau yang layak, dikatakan bahawa terdapat penyelesaian yang tidak terhingga. Kes ini berlaku jika cerun garis-Binefits adalah sama dengan mana-mana baris lain yang mengehadkan rantau ini.

Untuk pastri kami, simpang calon adalah A, B dan C.

- Kaedah Simplex Dantzig

Kaedah grafik atau geometri boleh digunakan untuk dua pembolehubah. Walau bagaimanapun, ia lebih rumit apabila terdapat tiga pembolehubah, dan mustahil untuk digunakan untuk bilangan pembolehubah yang lebih besar.

Ketika menghadapi masalah lebih dari dua pembolehubah, Kaedah simplex, yang terdiri daripada satu siri algoritma untuk mengoptimumkan fungsi objektif. Matriks mudah dan aritmetik biasanya digunakan untuk menjalankan pengiraan.

Kaedah simplex bermula dengan memilih penyelesaian yang layak dan memeriksa jika ia optimum. Sekiranya kita telah menyelesaikan masalah ini, tetapi jika tidak, ia terus ke arah penyelesaian yang lebih dekat dengan pengoptimuman. Sekiranya penyelesaiannya wujud, algoritma dengannya dalam beberapa percubaan.

Boleh melayani anda: berapakah julat statistik? (Dengan contoh)

Aplikasi

Pengaturcaraan linear dan bukan linear yang digunakan dalam banyak bidang untuk membuat keputusan terbaik dalam mengurangkan kos dan meningkatkan keuntungan, yang tidak selalu monetari, kerana ia dapat diukur dalam masa, sebagai contoh, jika anda berusaha untuk meminimumkan masa yang diperlukan untuk melaksanakan satu siri operasi.

Berikut adalah beberapa bidang:

-Dalam pemasaran ia digunakan untuk mencari gabungan media terbaik (rangkaian sosial, televisyen, akhbar dan lain -lain) untuk mengiklankan produk tertentu.

-Untuk peruntukan kerja yang sesuai dengan kakitangan syarikat atau kilang atau jadual kepada mereka.

-Dalam pemilihan makanan yang paling berkhasiat dan pada kos terendah dalam industri ternakan dan ternakan.

Latihan yang diselesaikan

- Latihan 1

Graf model pengaturcaraan linear yang dibangkitkan di bahagian sebelumnya.

Penyelesaian

Adalah perlu untuk menggambarkan set nilai yang ditentukan oleh sistem sekatan yang dinyatakan dalam masalah:

1. x ≥ 0
2. dan ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 dan ≤ 10

Rantau yang diberikan oleh Insquations 1 dan 2 sepadan dengan kuadran pertama pesawat Cartesian. Bagi Intquations 3 dan 4, ia bermula dengan mencari garis sekatan:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

Rantau yang boleh dilaksanakan adalah segi empat segi yang mana titiknya adalah titik A, B, C dan D dan D.

Keuntungan minimum ialah 0, oleh itu baris 8x + 10 dan 10 adalah had yang lebih rendah dan garisan ISO -Benefit telah menunggu -8/10 = -0.8.

Nilai ini berbeza dari lereng garis sekatan yang lain dan sebagai kawasan yang boleh dilaksanakan terhad, terdapat penyelesaian yang unik.

Rajah 5. Penyelesaian Grafik Latihan 1, menunjukkan rantau yang layak dan penyelesaian titik C di salah satu simpang di rantau tersebut. Sumber: f. Zapata.

Penyelesaian ini sepadan dengan garis cerun -0.8 yang melewati salah satu mata a, b atau c, yang koordinatnya adalah:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Penyelesaian optimum

Kami mengira nilai g untuk setiap perkara ini:

-(11; 5.625): g_Ke = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): g_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): g_C = 8 x 16 + 10 x 0 = 128

Keuntungan terbesar ialah pembuatan 11 kek hutan hitam dan 5.625 Kek Sacripantine. Penyelesaian ini bersetuju dengan yang ditemui melalui perisian.

- Latihan 2

Sahkan hasil latihan sebelumnya dengan menggunakan fungsi Solver (Penyelesaian) yang terdapat dalam kebanyakan spreadsheet seperti Excel atau Calc de LibreOffice, yang menggabungkan algoritma simplex untuk pengoptimuman pengaturcaraan linear.

Penyelesaian

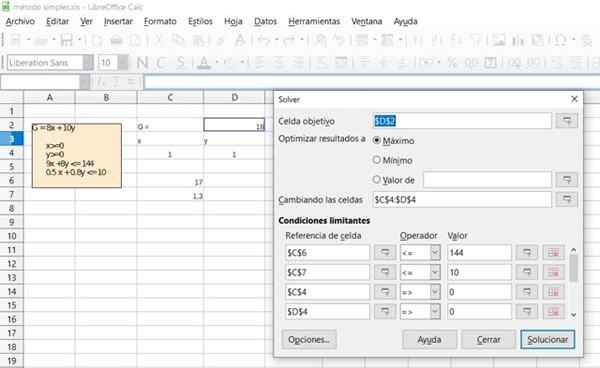Rajah 6. Perincian Penyelesaian Latihan 1 melalui Spreadsheet Calc Pejabat Percuma. Sumber: f. Zapata. 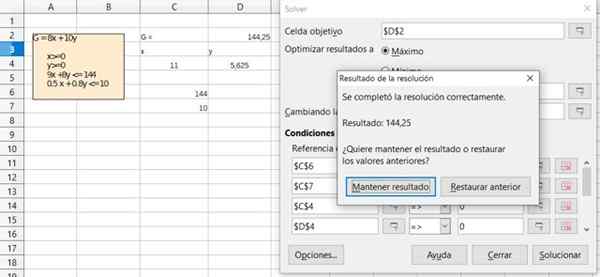Rajah 7. Perincian Penyelesaian Latihan 1 melalui Spreadsheet Calc Pejabat Percuma. Sumber: f. Zapata.

Rujukan

1. Cemerlang. Pengaturcaraan linear. Pulih dari: cemerlang.org.
2. Eppen, g. 2000. Penyelidikan Operasi dalam Sains Pentadbiran. 5th. Edisi. Prentice Hall.
3. Haeussler, e. 1992. Matematik untuk Pentadbiran dan Ekonomi. 2. Edisi. Kumpulan editorial Ibero -Amerika.
4. Hiru.Eus. Pengaturcaraan linear. Pulih dari: hiru.Eus.
5. Wikipedia. Pengaturcaraan linear. Pulih dari: Adakah. Wikipedia.org.