Penjelasan Proporsionaliti Komposit, Tiga Peraturan Kompaun, Latihan

The Komposit atau berkadar berbilang Ini adalah hubungan antara lebih daripada dua magnitud, di mana perkadaran langsung dan songsang dapat dilihat antara data dan yang tidak diketahui. Ini adalah versi yang lebih maju dari perkadaran mudah, walaupun teknik yang digunakan dalam kedua -dua prosedur adalah serupa.

Sebagai contoh, jika 7 orang diperlukan untuk memuat turun 10 tan barangan dalam 3 jam, perkadaran kompaun boleh digunakan untuk mengira berapa banyak orang yang diperlukan untuk memuat turun 15 tan dalam 4 jam.

Sumber: Pixabay.com

Untuk menjawab soalan ini, mudah untuk membuat jadual nilai untuk mengkaji dan mengaitkan magnitud dan tidak diketahui.

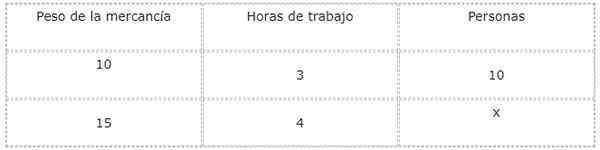
Jenis hubungan antara setiap magnitud dan yang tidak diketahui sekarang dianalisis, yang dalam kes ini sepadan dengan bilangan orang yang akan bekerja.

Oleh kerana berat barangan meningkat, bilangan orang yang diperlukan untuk memuat turun juga meningkat. Oleh sebab itu, hubungan antara berat badan dan pekerja langsung.

Sebaliknya, dengan meningkatkan bilangan pekerja, waktu kerja berkurangan. Kerana ini, hubungan antara orang dan waktu bekerja adalah songsang.

[TOC]

Cara mengira berkadar kompaun

Untuk menyelesaikan contoh -contoh seperti yang sebelumnya, kaedah tiga peraturan kompaun kebanyakannya digunakan. Ini terdiri daripada mewujudkan jenis hubungan antara magnitud dan tidak diketahui dan kemudian mewakili produk antara pecahan.

Berkenaan dengan contoh awal, pecahan yang sepadan dengan jadual nilai dianjurkan seperti berikut:

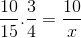
Tetapi sebelum menyelesaikan dan membersihkan yang tidak diketahui, pecahan yang sepadan dengan hubungan songsang mesti diterbalikkan. Bahawa untuk kes ini sesuai dengan pemboleh ubah masa. Dengan cara ini, operasi yang akan diselesaikan adalah:

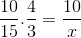
Yang satu -satunya perbezaan adalah pelaburan pecahan yang sepadan dengan masa pembolehubah 4/3. Nilai x dikendalikan dan jelas.

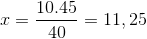
Oleh itu, lebih daripada sebelas orang diperlukan untuk memuat turun 15 tan barangan dalam 4 jam atau kurang.

Penjelasan

Perkadaran adalah hubungan yang berterusan antara magnitud yang tertakluk kepada perubahan, yang akan menjadi simetri bagi setiap magnitud yang terlibat. Terdapat hubungan berkadar secara langsung dan terbalik, dengan itu menentukan parameter perkadaran sederhana atau kompaun.

Mengarahkan tiga peraturan

Ia terdiri daripada nisbah perkadaran antara pembolehubah, yang menunjukkan tingkah laku yang sama apabila diubah suai. Sangat kerap dalam pengiraan peratusan yang berkaitan dengan magnitud yang berlainan seratus, di mana struktur asasnya dihargai.

Sebagai contoh, anda boleh mengira 15% daripada 63. Pada pandangan pertama, peratusan berkata tidak dapat dilihat dengan cara yang mudah. Tetapi melaksanakan peraturan tiga anda boleh membuat hubungan berikut: jika 100% adalah 63, maka 15%, berapa banyak yang akan berlaku?

Boleh melayani anda: Teorem Faktor: Penjelasan, Contoh, Latihan

100%-63

15%-x

Dan operasi yang sepadan adalah:

(lima belas% . 63) / 100% = 9.45

Di mana tanda peratusan dipermudahkan dan angka 9.45 yang mewakili 15% daripada 63 dicapai.

Tiga peraturan songsang

Seperti namanya, dalam hal ini hubungan antara pembolehubah adalah bertentangan. Hubungan songsang mesti diwujudkan sebelum meneruskan pengiraan. Prosedurnya adalah homolog kepada tiga peraturan langsung, kecuali pelaburan dalam pecahan yang akan dikira.

Contohnya, 3 pelukis memerlukan 5 jam untuk menyelesaikan dinding. Berapa jam 4 pelukis selesai?

Dalam hal ini hubungan itu terbalik, kerana dengan meningkatkan bilangan pelukis waktu kerja harus berkurang. Hubungan itu ditubuhkan;

3 pelukis - 5 jam

4 pelukis- x jam

Apabila hubungan itu terbalik, susunan operasi dibalikkan. Ini adalah cara yang betul;

(3 pelukis) . (5 jam) / 4 pelukis = 3.75 jam

Istilah pelukis dipermudahkan, dan hasilnya adalah 3.75 jam.

Keadaan

Untuk berada di hadapan sebatian atau pelbagai perkadaran, perlu mencari kedua -dua jenis hubungan antara magnitud dan pembolehubah.

- Langsung: Pembolehubah membentangkan tingkah laku yang sama seperti yang tidak diketahui. Iaitu, dengan peningkatan atau penurunan satu, yang lain diubah sama rata.

- Songsang: pemboleh ubah memberikan tingkah laku antonim kepada yang tidak diketahui. Pecahan yang mentakrifkan pembolehubah ini dalam jadual nilai mesti dibalikkan, untuk mewakili hubungan berkadar terbalik antara pembolehubah dan tidak diketahui.

Pengesahan hasil

Adalah sangat biasa untuk mengelirukan urutan magnitud ketika bekerja dengan berkadar kompaun, tidak seperti apa yang berlaku dalam pengiraan perkadaran biasa, yang sifatnya kebanyakannya langsung dan resoluble dengan cara tiga peraturan yang mudah.

Oleh itu, adalah penting untuk mengkaji susunan logik hasilnya, mengesahkan kesesuaian angka -angka yang dibuang oleh tiga peraturan kompaun.

Dalam contoh awal, membuat kesilapan ini akan menyiratkan 20 hasilnya. Iaitu 20 orang untuk memuat turun 15 tan barangan dalam 4 jam.

Pada pandangan pertama ia tidak kelihatan seperti hasil gila, tetapi peningkatan hampir 200% kakitangan (dari 7 hingga 20 orang) adalah penasaran apabila kenaikan barangan adalah 50%, dan walaupun dengan margin masa yang lebih besar untuk melaksanakannya bekerja.

Ia boleh melayani anda: Persamaan Parabola Umum (contoh dan latihan)

Dengan cara ini, pengesahan logik hasilnya merupakan langkah penting dengan melaksanakan tiga peraturan kompaun.

Pelepasan

Walaupun sifat yang lebih asas mengenai pembentukan matematik, pelepasan merupakan langkah penting dalam kes -kes yang berkadar. Pelepasan yang salah cukup untuk membatalkan apa -apa keputusan yang diperoleh mengikut tiga kompaun sederhana atau.

Sejarah

Peraturan tiga menjadi terkenal di Barat melalui Arab, dengan penerbitan oleh beberapa penulis. Antara mereka al-jwarizmi dan al-biruni.

Al-Biruni, terima kasih kepada pengetahuan multikulturalnya, mempunyai akses kepada maklumat yang luas mengenai amalan ini dalam perjalanannya ke India, yang bertanggungjawab untuk dokumentasi yang paling luas mengenai tiga peraturan tiga.

Ia menimbulkan siasatannya, bahawa India adalah tempat pertama di mana penggunaan tiga peraturan itu dibuat bersama. Penulis memberi jaminan bahawa ia dibuat dengan lancar dalam versi langsung, songsang dan bahkan yang terdiri daripada.

Tarikh tepat di mana ketiga -tiga peraturan itu menjadi sebahagian daripada pengetahuan matematik India masih belum diketahui. Walau bagaimanapun, dokumen tertua yang bertujuan untuk amalan ini, manuskrip Bakhshali, ditemui pada tahun 1881. Kini berada di Oxford.

Banyak ahli sejarah matematik memastikan bahawa manuskrip ini bermula dari awal era sekarang.

Latihan yang diselesaikan

Latihan 1

Syarikat penerbangan mesti bergerak 1535 orang. Diketahui bahawa dengan 3 pesawat diperlukan 12 hari untuk dibawa ke penumpang terakhir ke destinasi. 450 Lebih banyak orang telah mencapai syarikat penerbangan dan 2 pesawat diperintahkan untuk bekerjasama dengan tugas ini. Berapa hari syarikat penerbangan akan dibawa ke penumpang terakhir ke destinasinya?

Hubungan antara bilangan orang dan hari kerja adalah langsung, kerana lebih banyak orang, lebih banyak hari diperlukan untuk menjalankan kerja ini.

Sebaliknya, hubungan antara kapal terbang dan hari berkadar songsang. Dengan meningkatkan jumlah kapal terbang, hari yang diperlukan berkurangan untuk dipindahkan kepada semua penumpang.

Jadual nilai yang merujuk kepada kes ini dijalankan.

Seperti yang terperinci dalam contoh awal, pengangka dan penyebut mesti dilaburkan dalam pecahan yang sepadan dengan pemboleh ubah terbalik berkenaan dengan yang tidak diketahui. Meninggalkan operasi seperti berikut:

Boleh melayani anda: Pengiraan pendekatan menggunakan perbezaan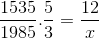

X = 71460/7675 = 9.31 hari

Untuk bergerak ke tahun 1985 orang menggunakan 5 pesawat, lebih dari 9 hari diperlukan.

Latihan 2

Harvest jagung 25 -ton dibawa ke trak kargo. Diketahui bahawa tahun sebelumnya mengambil masa 8 jam dengan gaji 150 pekerja. Sekiranya untuk tahun ini gaji meningkat 35%, berapa lama masa yang diperlukan untuk mengisi trak beban dengan penuaian 40 -ton?

Sebelum mewakili jadual nilai, bilangan pekerja untuk tahun ini mesti ditakrifkan. Ini meningkat 35% daripada angka awal 150 pekerja. Untuk ini, tiga peraturan langsung digunakan.

100% - 150

35% - x

X = (35 . 100)/100 = 52.5. Ini adalah bilangan pekerja tambahan berkenaan dengan tahun sebelumnya, memperoleh jumlah 203 pekerja, tidak berpuas hati untuk mengelilingi jumlah yang diperoleh.

Jadual data yang sepadan ditakrifkan

Untuk kes ini, beratnya mewakili pemboleh ubah hubungan langsung dengan masa yang tidak diketahui. Sebaliknya, pemboleh ubah pekerja menguruskan hubungan songsang dengan masa. Sebilangan besar pekerja, hari akan lebih pendek.

Mengambil kira pertimbangan ini dan melabur pecahan yang sepadan dengan pekerja, ia dikira.

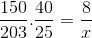
X = 40600/6000 = 6.76 jam

Hari akan mengambil masa kurang dari 7 jam.

Latihan yang dicadangkan

- Tentukan 73% daripada 2875.

- Kirakan jumlah jam yang teresa tidur, jika diketahui bahawa hanya 7% dari jumlah tidur hari. Tentukan berapa jam tidur seminggu.

- Akhbar awam 2000 setiap 5 jam, hanya menggunakan 2 mesin cetak. Berapa banyak salinan yang akan dihasilkan dalam 1 jam, jika anda menggunakan 7 mesin? Berapa lama akan menghasilkan 10.000 salinan menggunakan 4 mesin?

Rujukan

1. Encyclopedia Alvarez-Iniciacion. Ke. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
2. Lengkap Manual Arahan Utama Elemental dan Superior: Untuk penggunaan pemohon kepada guru dan terutama pelajar sekolah provinsi biasa, Jilid 1. Joaquín Avendaño. Percetakan d. Dionisio Hidalgo, 1844.
3. Penghampiran penarafan fungsi sebenar. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 Mac. 2011.
4. Aritmetik Elemental untuk Pengajaran di Sekolah dan Sekolah di Amerika Tengah. Darío González. Petua. Arenales, 1926.
5. Kajian Matematik: Mengenai Kajian dan Kesukaran Matematik. Augustus de Morgan. Baldwin dan Cradock, 1830.