Berapakah julat statistik? (Dengan contoh)

Dia julat, Lawatan atau amplitud, dalam statistik, adalah perbezaan (penolakan) antara nilai maksimum dan nilai minimum satu set data dari sampel atau populasi. Sekiranya julat dengan huruf r dan data diwakili dengan cara x, Formula untuk julat adalah semata -mata:

R = x_maks - x_min

 Di mana x_maks Ia adalah nilai maksimum data dan x_min Ia adalah minimum.

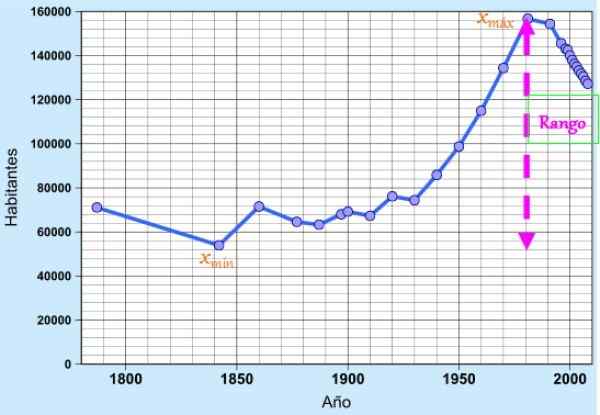
Rajah 1. Julat data yang sepadan dengan penduduk Cádiz dalam dua abad yang lalu. Sumber: Wikimedia Commons.

Konsep ini sangat berguna sebagai ukuran penyebaran mudah untuk dengan cepat menghargai kebolehubahan data, kerana ia menunjukkan lanjutan atau panjang selang di mana ini dijumpai.

Contohnya, katakan kedudukan sekumpulan 25 pelajar lelaki pada tahun pertama kejuruteraan di sebuah universiti. Pelajar tertinggi dalam kumpulan mengukur 1.93 m dan paling rendah 1.67 m. Ini adalah nilai ekstrem data sampel, oleh itu laluannya adalah:

R = 1.93 - 1.67 m = 0.26 m atau 26 cm.

Kedudukan pelajar kumpulan ini diedarkan sepanjang julat ini.

[TOC]

Kelebihan dan kekurangan

Julatnya, seperti yang kita katakan sebelumnya, ukuran bagaimana tersebar adalah data. Julat kecil menunjukkan bahawa data lebih kurang dekat dan penyebarannya sedikit. Sebaliknya, julat yang lebih besar menunjukkan bahawa data lebih tersebar.

Kelebihan mengira julatnya jelas: ia sangat mudah dan pantas dicari, kerana ia adalah perbezaan yang mudah.

Ia juga mempunyai unit yang sama dengan data yang berfungsi dan konsepnya sangat mudah untuk mentafsir untuk mana -mana pemerhati.

Dalam contoh kedudukan pelajar kejuruteraan, jika julatnya adalah 5 cm, kita akan mengatakan bahawa pelajar adalah saiz yang sama. Tetapi dengan julat 26 cm, kami segera mengandaikan bahawa dalam sampel terdapat pelajar semua statur perantaraan. Adakah andaian ini selalu betul?

Ia dapat melayani anda: perbezaan antara bulatan dan lilitan (dengan contoh)

Kekurangan julat sebagai ukuran penyebaran

Sekiranya kita melihat dengan teliti, dalam sampel 25 pelajar kejuruteraan, hanya satu daripada mereka mengukur 1.93 dan baki 24 mempunyai statur hampir 1.67 m.

Namun julatnya tetap sama, walaupun sangat mungkin bahawa sebaliknya berlaku: bahawa kedudukan majoriti berayun sekitar 1.90 m dan hanya satu langkah 1.67 m.

Walau apa pun, pengedaran data sangat berbeza.

Kelemahan julat sebagai ukuran penyebaran adalah disebabkan oleh hakikat bahawa ia hanya menggunakan nilai yang melampau dan mengabaikan semua yang lain. Oleh kerana kebanyakan maklumat hilang, tidak ada idea bagaimana data sampel diedarkan.

Ciri lain yang penting ialah julat sampel tidak pernah berkurangan. Sekiranya kita menambah lebih banyak maklumat, iaitu, kita mempertimbangkan lebih banyak data, julat meningkat atau tetap sama.

Dan dalam apa jua keadaan, hanya berguna apabila bekerja dengan sampel kecil, penggunaan uniknya tidak disyorkan sebagai ukuran penyebaran dalam sampel besar.

Apa yang perlu dilakukan ialah melengkapkan pengiraan langkah -langkah penyebaran lain yang mengambil kira maklumat yang disediakan oleh jumlah data: Laluan Interquartilic, varians, sisihan piawai dan pekali variasi.

Laluan interquirile, kuartil dan contoh yang diselesaikan

Kami telah menyedari bahawa kelemahan julat sebagai ukuran penyebaran adalah bahawa ia hanya menggunakan nilai ekstrem pengedaran data, tidak menghilangkan yang lain.

Untuk mengelakkan kesulitan ini, kuartil: tiga nilai yang dikenali sebagai Langkah -langkah kedudukan.

Mereka mengedarkan data yang tidak dikumpulkan ke dalam empat bahagian (langkah -langkah kedudukan yang digunakan secara meluas adalah Deciles dan juga persentil). Ini adalah ciri -cirinya:

-Qartil pertama q₁ Ia adalah nilai data sehingga 25 % dari semuanya kurang dari q₁.

Boleh melayani anda: pemalar berkadar: apakah, pengiraan, latihan

-Qartil kedua q₂ Ia adalah median pengedaran, yang bermaksud bahawa separuh (50 %) data kurang daripada nilai tersebut.

-Akhirnya kuartil ketiga q₃ menunjukkan bahawa 75 % data kurang daripada q₃.

Kemudian, julat interquotil atau laluan interquartile ditakrifkan sebagai perbezaan antara kuartil ketiga q₃ dan kuartil pertama q₁ data:

Perjalanan interquotil = r_Q = Q₃ - Q₁

Dengan cara ini, nilai pangkat r_Q Ia tidak terjejas oleh nilai yang melampau. Oleh itu, adalah dinasihatkan untuk menggunakannya apabila ia berkaitan dengan pengagihan berat sebelah, seperti pelajar yang sangat tinggi atau sangat rendah yang diterangkan di atas.

- Pengiraan Cuartyles

Terdapat beberapa cara untuk mengira mereka, di sini kami akan mencadangkan satu, tetapi dalam apa jua keadaan, perlu mengetahui bilangan pesanan "N_{Sama ada}", Yang merupakan tempat yang menduduki kuartil masing -masing dalam pengedaran.

Iaitu, jika contohnya istilah yang sepadan dengan q₁ adalah yang kedua, ketiga atau keempat dan sebagainya.

Kuartil pertama

N_{Sama ada} (Q₁) = (N+1) / 4

Kuartil kedua atau median

N_{Sama ada} (Q₂) = (N+1) / 2

Kuartil ketiga

N_{Sama ada} (Q₃) = 3 (n+1) / 4

Di mana n ialah nombor data.

Median adalah nilai yang betul di tengah -tengah pengedaran. Sekiranya nombor data ganjil tidak ada masalah dalam mencarinya, tetapi jika ia walaupun, maka kedua -dua nilai pusat adalah purata untuk menjadikannya satu.

Sebaik sahaja nombor pesanan dikira, salah satu daripada tiga peraturan ini diikuti:

-Sekiranya anda tidak mempunyai perpuluhan, data yang ditunjukkan dalam pengedaran dicari dan ini akan dicari keempat.

-Apabila nombor pesanan berada di antara dua, maka data yang ditunjukkan oleh seluruh bahagian dengan fakta berikut adalah purata, dan hasilnya adalah kuartil yang sepadan.

-Dalam mana -mana kes lain, integer terdekat adalah bulat dan itu akan menjadi tempat keempat.

Boleh melayani anda: prinsip aditif

Contoh yang diselesaikan

Pada skala 0 hingga 20, sekumpulan 16 pelajar matematik saya memperoleh gred berikut (mata) dalam peperiksaan separa:

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14

Cari:

a) Laluan data atau data.

b) Nilai kuartil q₁ dan q₃

c) julat interquartil.

Rajah 2. Adakah kelayakan peperiksaan matematik ini melakukan banyak kebolehubahan? Sumber: Pixabay.

Penyelesaian kepada

Perkara pertama yang perlu dilakukan untuk mencari laluan adalah untuk memerintahkan data yang semakin meningkat atau berkurang. Contohnya dalam peningkatan susunan yang anda ada:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Melalui formula yang diberikan pada permulaan: r = x_maks - x_min

R = 20 - 1 mata = 19 mata.

Menurut hasilnya, gred ini mempunyai penyebaran yang hebat.

Penyelesaian b

N = 16

N_{Sama ada} (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

Ia adalah nombor dengan perpuluhan, yang seluruhnya adalah 4. Kemudian kita pergi ke pengedaran, data yang menduduki tempat keempat dicari dan nilainya adalah purata dengan kedudukan kelima. Kerana kedua -duanya adalah 9, purata juga 9 dan kemudian:

Q₁ = 9

Sekarang kita mengulangi prosedur untuk mencari q₃:

N_{Sama ada} (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Sekali lagi ia adalah perpuluhan, tetapi kerana ia tidak di tengah -tengahnya dibundarkan hingga 13. Kuartil yang dicari menduduki kedudukan tiga belas dan adalah:

Q₃ = 16

Penyelesaian c

R_Q = Q₃ - Q₁ = 16 - 9 = 7 mata.

Seperti yang kita lihat jauh lebih rendah daripada julat data yang dikira dalam Bahagian A), kerana penarafan minimum adalah 1 mata, nilai jauh dari yang lain.

Rujukan

1. Berenson, m. 1985. Statistik untuk Pentadbiran dan Ekonomi. Inter -American s.Ke.
2. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
3. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
4. Contoh kuartil. Diperolehi dari: Matematik10.jaring.
5. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
6. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.