Formula dan persamaan yang diperlukan, contoh, senaman

The Penilaian yang berkhayal, Varians quasi atau varians yang tidak sihat adalah ukuran statistik penyebaran data a Contoh Mengenai purata. Sampel seterusnya terdiri daripada satu siri data yang diambil dari alam semesta utama, yang dipanggil penduduk.

Ia dilambangkan dalam beberapa cara, di sini ia telah dipilih s_c² Dan untuk mengira, formula berikut berikut:

Rajah 1. Takrifan quasiveness. Sumber: f. Zapata.

Di mana:

-s_c ² = quasirance atau varians sampel (varians sampel)

-x_Yo = Setiap data sampel

-n = bilangan pemerhatian

-X = Purata sampel

Oleh kerana perpaduan sampel quasiveness adalah kuadrat unit di mana sampel datang, pada masa mentafsirkan hasilnya, lebih disukai untuk bekerja dengan sisihan piawai quasi atau sisihan standard sampel.

Ini dilambangkan sebagai s_c Dan ia diperoleh dengan mengekstrak akar kuasi kuasi:

s_c = √ s_c ²

Quasiriance serupa dengan varians s², dengan satu -satunya perbezaan yang dalam penyebutnya adalah N-1, sementara dalam varians hanya dibahagikan dengan n. Jelas bahawa apabila n sangat besar, nilai -nilai kedua -duanya cenderung sama.

Apabila nilai quasiriance diketahui, anda dapat mengetahui dengan segera tentang varians.

[TOC]

Contoh -contoh kebencian

Anda ingin mengetahui ciri -ciri mana -mana penduduk: orang, haiwan, tumbuh -tumbuhan dan pada umumnya apa -apa jenis objek. Tetapi menganalisis seluruh penduduk mungkin bukan tugas yang mudah, terutamanya jika bilangan elemen sangat besar.

Kemudian sampel diambil, dengan harapan bahawa tingkah laku mereka mencerminkan penduduk dan dengan itu dapat membuat kesimpulan mengenainya, terima kasih kepada sumber yang dioptimumkan. Ini dikenali sebagai inferens statistik.

Berikut adalah beberapa contoh di mana quasiriance dan sisihan piawai yang berkaitan dengan kuasi berfungsi sebagai penunjuk statistik dengan menunjukkan bahawa hasil yang diperoleh berkenaan dengan purata.

Ia dapat melayani anda: perimeter bulatan: Cara mengeluarkannya dan formula, latihan diselesaikan

1.- Pengarah pemasaran sebuah syarikat yang mengeluarkan bateri kereta perlu menganggarkan, dalam beberapa bulan, purata tempoh bateri.

Untuk melakukan ini, secara rawak pilih sampel 100 bateri jenama yang dibeli. Syarikat itu mengekalkan rekod data pembeli dan boleh menemuinya untuk mengetahui tempoh bateri.

Rajah 2. Penilaian cuasive berguna untuk membuat kesimpulan dan kawalan kualiti. Sumber: Pixabay.

2.- Pengurusan akademik institusi universiti perlu menganggarkan pendaftaran tahun berikutnya, menganalisis bilangan pelajar yang dijangka meluluskan subjek yang ada sekarang.

Sebagai contoh, setiap bahagian yang kini mengkaji subjek fizikal I, alamat boleh memilih sampel pelajar dan menganalisis prestasinya di kerusi tersebut. Dengan cara ini, anda dapat menyimpulkan berapa banyak pelajar yang akan mempelajari Fizik II dalam tempoh yang akan datang.

3.- Sekumpulan ahli astronomi memfokuskan perhatian mereka di bahagian langit, di mana sejumlah bintang dengan ciri -ciri tertentu diperhatikan: saiz, jisim dan suhu misalnya.

Perlu ditanya sama ada bintang -bintang di rantau lain yang sama akan mempunyai ciri -ciri yang sama, termasuk bintang -bintang di galaksi lain, seperti awan jiran Magallanes atau Andromeda.

Mengapa membahagikan antara n-1?

Dalam quasiriance dibahagikan antara N-1 bukan n Dan itu kerana quasiriance adalah Menegaskan penganggar, Seperti yang dinyatakan pada awal.

Ia berlaku dari populasi yang sama adalah mungkin untuk mengeluarkan banyak sampel. Varians setiap sampel ini juga boleh diasaskan, tetapi purata variasi ini tidak sama dengan varians penduduk.

Boleh melayani anda: nilai relatif

Malah, purata variasi sampel cenderung meremehkan varians penduduk, kecuali jika ia digunakan N-1 Dalam penyebut. Dapat disahkan bahawa nilai yang dijangkakan dari kebencian e (s_c²) tepat s².

Itulah sebabnya dikatakan bahawa quasiriance adalah insented dan merupakan penganggar yang lebih baik dari varians penduduk s².

Cara alternatif untuk mengira penilaian yang berkekalan

Ia mudah menunjukkan bahawa quasiriance juga boleh dikira seperti berikut:

s_c² = [Σx² / (N -1)] - [Σnx² / (N-1)]

Skor standard

Dengan mempunyai sisihan dari sampel, kita dapat mengetahui berapa banyak sisihan piawai mempunyai nilai tertentu x, sama ada di atas atau di bawah purata.

Untuk ini, ungkapan tanpa dimensi berikut digunakan:

Skor standard = (x - x) / s_c

Latihan diselesaikan

Hitung quasiriance dan sisihan quasi -tipikal data berikut, yang terdiri daripada pembayaran bulanan dalam $ dibuat oleh syarikat insurans ke klinik swasta.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Gunakan definisi kebencian yang diberikan pada mulanya dan juga mengesahkan hasilnya dengan bentuk alternatif yang diberikan di bahagian sebelumnya.

b) Kirakan skor standard data kedua, membaca dari atas ke bawah.

Penyelesaian kepada

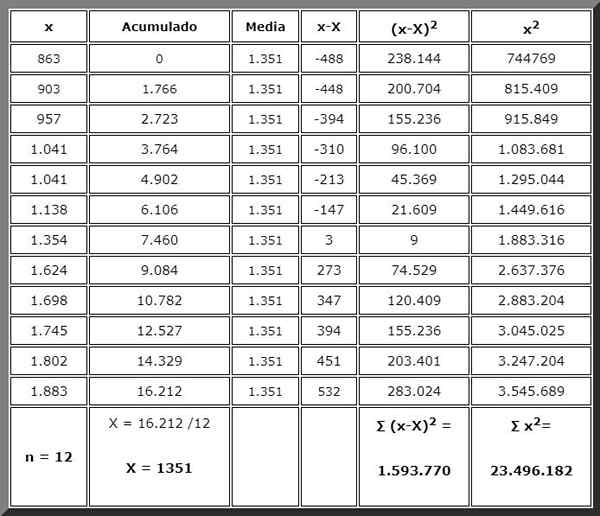
Masalahnya dapat diselesaikan dengan tangan dengan bantuan kalkulator sederhana atau saintifik, yang harus kita teruskan dengan teratur. Dan untuk ini tidak lebih baik daripada mengatur data dalam jadual seperti yang ditunjukkan di bawah:

Terima kasih kepada jadual yang anda telah menganjurkan maklumat dan jumlah yang diperlukan dalam formula berada di akhir lajur masing -masing, bersedia untuk digunakan dengan segera. Summasi ditunjukkan dengan berani.

Boleh melayani anda: Apakah 7 elemen lilitan?

Lajur purata sentiasa diulang, tetapi ia berbaloi kerana mudah untuk mempunyai nilai yang dilihat, untuk mengisi setiap baris meja.

Akhirnya, persamaan untuk quasirance yang diberikan pada mulanya digunakan, hanya nilai -nilai yang diganti dan dari segi jumlah, kita sudah mengira:

s_c² = 1.593.770 / (12-1) = 1.593.770/11 = 144.888.2

Ini adalah nilai quasiriance dan unitnya adalah "dolar kuadrat", yang tidak membuat banyak rasa praktikal, jadi quasides standard sampel dikira, yang tidak lebih dari akar kuasi kuasi:

s_c = (√144.888.2) $ = 380.64 $

Segera disokong bahawa nilai ini juga diperolehi dengan bentuk alternatif quasivariance. Jumlah yang diperlukan adalah di hujung lajur terakhir di sebelah kiri:

s_c² = [Σx² / (N-) - [Σnx² / (N-1)] = [23.496.182/11] - [12 x 1351²/ sebelas]

= 2.136.016.55 - 1.991.128,36 = 144.$ 888 Squared

Ia adalah nilai yang sama yang diperoleh dengan formula yang diberikan pada awalnya.

Penyelesaian b

Nilai kedua dari atas ke bawah ialah 903, skor standardnya adalah

Skor standard 903 = (x - x) / s_c = (903 - 1351)/380.64 = -1.177

Rujukan

1. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
2. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
3. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
4. Langkah -langkah penyebaran. Pulih dari: Thales.Cica.adalah.
5. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.