Langkah -langkah kecenderungan utama untuk formula data dikumpulkan, latihan

The Langkah -langkah trend pusat Mereka menunjukkan nilai di mana data pengedaran. Yang paling terkenal ialah purata purata atau aritmetik, yang terdiri daripada menambahkan semua nilai dan membahagikan hasilnya dengan jumlah data.

Walau bagaimanapun, jika pengedaran terdiri daripada sejumlah besar nilai dan tidak dibentangkan secara teratur, tidak mudah untuk melakukan pengiraan yang diperlukan untuk mengekstrak maklumat berharga yang mereka ada.

Rajah 1. Langkah -langkah kecenderungan utama untuk data dikumpulkan adalah petunjuk yang baik dari tingkah laku data umum

Itulah sebabnya mereka dikelompokkan ke dalam kelas atau kategori, untuk menghuraikan a pengedaran Frekuensi. Menjalankan urutan data sebelumnya ini, maka lebih mudah untuk mengira langkah -langkah kecenderungan pusat, antaranya:

-Separuh

-Median

-Fesyen

-Maksud geometri

-Maksud harmonik

Formula

Di bawah ini kita mempunyai formula langkah -langkah kecenderungan pusat untuk data dikumpulkan:

Purata aritmetik

Purata adalah yang paling digunakan untuk mencirikan data kuantitatif (nilai berangka), walaupun ia agak sensitif terhadap nilai pengedaran yang melampau. Ia dikira oleh:

Dengan:

-X: aritmetik purata atau purata

-F_Yo: kekerapan kelas

-m_Yo: Jenama kelas

-G: Nombor kelas

-N: Jumlah data

Median

Untuk mengira ia, adalah perlu untuk mencari selang yang mengandungi pemerhatian n/2 dan interpolar untuk menentukan nilai berangka pemerhatian tersebut, melalui formula berikut:

Di mana:

-C: lebar selang yang dimiliki median

-B_M: sempadan bawah selang waktu tersebut

-F_m: Bilangan pemerhatian yang terkandung dalam selang waktu

-N/2: Jumlah data dibahagikan dengan 2.

-F_BM: bilangan pemerhatian sebelum selang yang mengandungi median.

Oleh itu, median adalah ukuran kedudukan, iaitu, membahagikan data yang ditetapkan menjadi dua bahagian. Mereka juga boleh ditakrifkan kuartil, Deciles dan persentil, yang membahagikan pengedaran menjadi empat, sepuluh dan seratus bahagian masing -masing.

Boleh melayani anda: Transformasi Fourier: sifat, aplikasi, contoh

Fesyen

Dalam data dikumpulkan, kelas atau kategori yang mengandungi kebanyakan pemerhatian yang dicari. Ini adalah Kelas modal. Pengedaran mungkin mempunyai dua atau lebih fesyen, di mana ia dipanggil bimodal dan Multimodal, masing -masing.

Anda juga boleh mengira fesyen dalam data berkumpulan berikutan persamaan:

Dengan:

-L₁: Had bawah kelas di mana fesyen

-Δ₁: Ia kekal di antara kekerapan kelas modal dan kekerapan kelas yang mendahuluinya.

-Δ₂: tolak antara kekerapan kelas modal dan kekerapan kelas yang mengikutinya.

-C: Lebar selang yang mengandungi fesyen

Maksud harmonik

Maksud harmonik dilambangkan oleh h. Apabila anda mempunyai satu set n nilai x₁, x₂, x₃..., maksud harmoni adalah songsang atau timbal balik dari aritmetik min bagi songsang nilai -nilai.

Lebih mudah melihatnya melalui formula:

Dan apabila mempunyai data yang dikumpulkan, ungkapan itu berubah menjadi:

Di mana:

-H: Purata harmonik

-F_Yo: kekerapan kelas

-m_Yo: Jenama Kelas

-G: Nombor kelas

-N = f₁ + F₂ + F₃ +…

Maksud geometri

Jika anda mempunyai n Nombor positif x₁, x₂, x₃..., min geometri dikira oleh n-eme produk dari semua nombor:

Dalam kes data yang dikumpulkan, dapat ditunjukkan bahawa logaritma perpuluhan log purata geometri g, diberikan oleh:

Di mana:

-G: Maksud geometri

-F_Yo: kekerapan kelas

-m_Yo: Jenama kelas

-G: Nombor kelas

-N = f₁ + F₂ + F₃ +…

Hubungan antara h, g dan x

Memang benar bahawa:

H ≤ g ≤ x

Definisi yang paling banyak digunakan

Takrifan berikut adalah perlu untuk mencari nilai yang diterangkan dalam formula sebelumnya:

Kekerapan

Kekerapan ditakrifkan sebagai bilangan kali fakta diulang.

Julat

Ia adalah perbezaan antara nilai utama dan kecil, yang terdapat dalam pengedaran.

Bilangan kelas

Untuk mengetahui berapa banyak kelas yang kami kumpulan data, kami menggunakan beberapa kriteria, contohnya yang berikut:

Boleh melayani anda: 17 masalah yang beralasan

Sempadan

Nilai melampau setiap kelas atau selang dipanggil sempadan dan setiap kelas boleh mempunyai batas -batas yang ditentukan dengan baik, di mana ia mempunyai had yang lebih rendah dan satu lebih besar. Atau ia boleh mempunyai had terbuka, apabila julat diberikan, contohnya nilai lebih besar atau lebih rendah daripada bilangan tertentu.

Jenama Kelas

Ia hanya terdiri daripada titik tengah selang dan dikira dengan purata had atas dan had yang lebih rendah.

Lebar selang

Data boleh dikumpulkan ke dalam kelas yang sama atau berbeza, ini adalah lebar atau amplitud. Pilihan pertama adalah yang paling banyak digunakan, kerana ia memudahkan pengiraan, walaupun dalam beberapa kes adalah penting bahawa kelas mempunyai lebar yang berbeza.

Lebar c Dari selang waktu ia dapat ditentukan oleh formula berikut:

C = julat / n_c

Di mana_c Ia adalah bilangan kelas.

Latihan diselesaikan

Di bawah ini kita mempunyai satu siri pengukuran kelajuan dalam km/j, diambil dengan radar, yang sesuai dengan 50 kereta yang melalui jalan di bandar tertentu:

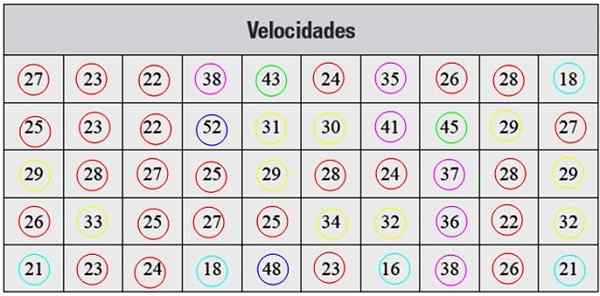Rajah 2. Jadual untuk latihan diselesaikan. Sumber: f. Zapata.

Penyelesaian

Data yang dibentangkan tidak dianjurkan, jadi langkah pertama adalah untuk mengelompokkannya ke dalam kelas.

Langkah -langkah untuk mengumpulkan data dan membina jadual

Langkah 1

Cari julat r:

R = (52 - 16) km/h = 36 km/j

Langkah 2

Pilih bilangan kelas n_c, Menurut kriteria yang diberikan. Oleh kerana terdapat 50 data, kita boleh memilih n_c = 6.

Langkah 3

Kirakan lebar c selang waktu:

C = julat /n_c = 36/6 = 6

Langkah 4

Borang kelas dan data kumpulan seperti berikut: Untuk kelas pertama had A yang lebih rendah dipilih sebaik sahaja nilai yang lebih rendah yang terdapat dalam jadual ditambah kepada nilai ini c = 6, yang sebelum ini dikira, dan dengan itu memperoleh had atas kelas pertama.

Ia meneruskan dengan cara yang sama untuk membina seluruh kelas, seperti yang ditunjukkan dalam jadual berikut:

Boleh melayani anda: Apakah nombor Capicúa? Sifat dan contoh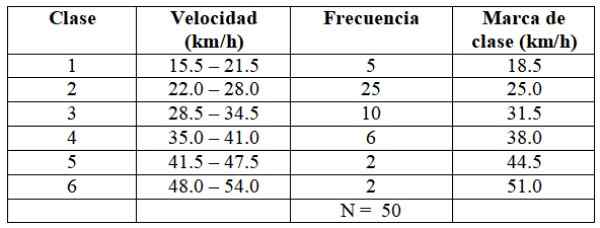

Setiap kekerapan sepadan dengan warna dalam Rajah 2, dengan cara ini ia memastikan bahawa tiada nilai melarikan diri dari yang diambil kira.

Pengiraan purata

X = (5 x 18.5 +25 x 25.0 + 10 x 31.5 + 6 x 38.0 + 2 x 44.5 + 2 x 51.0) ÷ 50 = 29.03 km/j

Pengiraan median

Median berada di kelas 2 jadual, kerana terdapat 30 data pengedaran pertama.

-Lebar selang yang mana median milik: c = 6

-Sempadan bawah selang di mana median adalah: b_M = 22.0 km/j

-Bilangan pemerhatian yang terkandung dalam selang f_m = 25

-Jumlah data dibahagikan dengan 2: 50/2 = 25

-Bilangan pemerhatian sebelum selang yang mengandungi median: f_BM = 5

Dan operasi adalah:

Median = 22.0 + [(25-5) ÷ 25] × 6 = 26.80 km/j

Fesyen

Fesyen juga terdapat dalam Kelas 2:

-Lebar selang: c = 6

-Had bawah kelas di mana fesyen dijumpai: l₁ = 22.0

-Tolak antara kekerapan kelas modal dan kekerapan kelas yang mendahuluinya: δ₁ = 25-5 = 20

-Tolak antara kekerapan kelas modal dan kekerapan kelas yang berikut: δ₂ = 25 - 10 = 15

Dengan data ini operasi adalah:

Fesyen = 22.0 + [20 ÷ (20 + 15)] x6 = 25.4 km/j

Pengiraan maksud geometri

N = f₁ + F₂ + F₃ +... = 50

log g = (5 x log 18.5 + 25 x log 25 + 10 x log 31.5 + 6 x log 38 + 2 × log 44.5 + 2 x log 51) /50 =

log g = 1.44916053

G = 28.13 km/j

Pengiraan purata harmonik

1/h = (1/50) x [(5/18.5) + (25/25) + (10/31.5) + (6/38) + (2/44.5) + (2/51)] = 0.0366

H = 27.32 km/j

Ringkasan langkah kecenderungan pusat

Unit pembolehubah adalah km/h:

-Media: 29.03

-Median: 26.80

-Fesyen: 25.40

-Media Geometri: 28.13

-Maksud Harmonik: 27.32

Rujukan

1. Berenson, m. 1985. Statistik untuk Pentadbiran dan Ekonomi. Inter -American s.Ke.
2. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
3. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
4. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
5. Spiegel, m. 2009. Statistik. Siri Schaum. 4 ta. Edisi. McGraw Hill.
6. Rawatan data berkumpulan. Pulih dari: gatal.Edu.mx.
7. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.