Apakah ungkapan algebra dan yang paling kerap?

The Ekspresi Algebra Mereka adalah istilah matematik yang mengandungi nombor dan huruf. Dalam kombinasi dengan simbol operasi matematik, mereka membenarkan mendapatkan formula atau persamaan, dari deskripsi yang dibuat oleh kata -kata. 

Sebaliknya, huruf tersebut boleh ditambah, dikurangkan, didarabkan atau dibahagikan dengan nombor lain, yang boleh jelas atau juga diwakili oleh huruf.

Rajah 1. Contoh ekspresi algebra

[TOC]

Apakah ungkapan algebra?

Contohnya ungkapan:

2x + 3 

Ini adalah ungkapan algebra, di mana huruf "x" mewakili nombor yang mungkin tidak diketahui atau yang boleh mengambil nilai yang berbeza.

Apakah kelebihan menggunakan ungkapan algebra dan bukannya berkata: "Dua kali nombor ditambah kepada 3"?

Pertama, ungkapan algebra menduduki ruang yang kurang. Dan kemudian, jika x bukan nombor tetap, nilai yang berbeza boleh diberikan kepada "x" untuk mendapatkan hasil yang berbeza dari ungkapan ini.

Ini dikenali sebagai nilai berangka ungkapan algebra.

Contohnya, jika x = 1 maka hasilnya ialah 2 ⋅1 + 3 = 2 + 3 = 5

Sebaliknya, melakukan x = -2, ungkapan ternyata 2 (-2) + 3 = -4 + 3 = -1

Dalam jenis aplikasi lain, ungkapan algebra mewakili persamaan atau kesamaan yang mesti diselesaikan untuk mengetahui nilai nombor yang diwakili oleh huruf tersebut.

Di sini kita mempunyai persamaan linear yang mudah:

2 ⋅x + 3 = 7

Penyelesaian kepada persamaan ini, yang dengan cara ini juga merupakan ungkapan algebra, adalah:

x = 2

Sejak mengalikan 2 by 2 memberikan 4 ditambah 3 memberikan hasilnya: 7. Tetapi lebih mudah difahami apabila ungkapan algebra digunakan dan bukannya menggambarkan segala -galanya dengan kata -kata.

Ungkapan algebra yang paling kerap

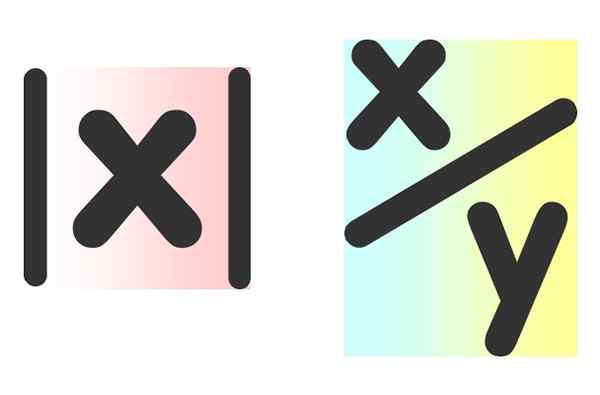Rajah 2. Jumlah yang tidak diketahui sering melambangkan dengan huruf "x" dan "y". Di sebelah kiri adalah nilai mutlak nombor dan di sebelah kanan kuota dalam dua nombor. Sumber: Pixabay.

Ekspresi algebra digunakan secara meluas dalam matematik, sains, ekonomi dan pentadbiran.

Berikut adalah senarai ungkapan yang kelihatan sangat kerap dalam matematik dan subjek lain, di mana cadangan diminta atau diselesaikan.

Ia dapat melayani anda: perimeter bulatan: Cara mengeluarkannya dan formula, latihan diselesaikan

Biasanya nombor yang tidak diketahui atau tidak diketahui dilambangkan sebagai "x", tetapi kita boleh menggunakan huruf abjad lain seperti yang dipersetujui.

Ia juga harus diingat bahawa dalam ungkapan algebra ia mungkin melibatkan lebih daripada satu nilai, tidak diketahui atau berubah, jadi masing -masing harus diberikan huruf yang berbeza.

Senarai Ekspresi Algebra

-Dua atau dua kali ganda nombor: 2x

-Duple dari bilangan lebih banyak unit: 2m + 3

-Bahagian ketiga nombor: z/3

-Dua kali nombor kecuali bahagian ketiga: 2x - x/3

-Kuadrat nombor: x²

-Kuadrat dari sejumlah nombor itu: x² + 2x

-Duple of the Square dari nombor: 2x²

-Nombor tork: 2n

-Nombor ganjil: 2n + 1

-Tiga nombor berturut -turut: x, (x+1), (x+2)

-Tiga nombor berturut -turut: 2n, 2n +2, 2n +4

-Tiga nombor ganjil berturut -turut, 2n + 1, 2n + 3, 2n + 5

-Bilangan tertentu ditambah kepada berturut -turut: x +(x +1) = 2x +1

-Separuh daripada berturut -turut integer: (x+1)/2

-Triple separuh kuadrat nombor: 3. (1/2) x² = (3/2) x²

-Separuh daripada satu lagi bilangan yang lain: x/2 + y/3

-Bahagian ketiga produk antara kuadrat nombor dan nombor lain yang mana unit itu dikurangkan: (1/3) x².(Y-1)

-Nombor dan sebaliknya: a, -a

-Nombor dan songsangnya: a, 1/a

-Jumlah nombor dengan berturut -turut ditinggikan ke dataran: x + (x + 1)²

-Tolak 7 pada dua kali ganda nombor tertentu tinggi ke dataran: (2x)² - 7

-Dua nombor yang apabila didarabkan memberi 24: p.Q = 24

Boleh melayani anda: anjakan sudut

-Nilai mutlak nombor: │x│

-Kota antara dua nombor: x/y

-Akar kuadrat dari produk dua nombor: √x.dan

Rajah 3. Ekspresi algebra ini dibaca sebagai "akar kuadrat produk dua nombor x dan y". Sumber: Pixabay.

-Satu nombor yang melebihi yang lain dalam 30 unit: x = y +30

-Dua kali nombor yang separuhnya dikurangkan: 2x- x/2

Masalah lisan dan ekspresi algebra mereka

- Masalah 1

Separuh daripada lembu beratnya 100 kg lebih daripada berat seperempat lembu yang sama. Berapakah berat lembu itu?

Jawapan

Untuk ekspresi algebra masalah ini, kami memanggil x berat lembu.

Separuh daripada lembu beratnya ½ x. Bahagian keempat lembu beratnya ¼ x. Akhirnya, ungkapan algebra yang sepadan dengan: "Separuh lembu beratnya 100 kg lebih daripada satu perempat" adalah:

½ x = ¼ x + 100

Untuk mengetahui berapa berat lembu, anda perlu mengumpulkan terma dengan x di sebelah kiri dan meninggalkan 100 ke kanan:

(½ -¼) x = 100

¼x = 100

x = 400 kg

Lembu beratnya 400 kg.

- Masalah 2

Di ladang bilangan arnab adalah dua kali lebih banyak lembu. Sekiranya bilangan lembu adalah 10. Berapa banyak arnab yang ada?

Jawapan

Jika c adalah bilangan arnab dan v adalah bilangan lembu, maka ungkapan algebra dari pernyataan itu adalah:

C = 2 ⋅ v

V = 10

Oleh itu, menggantikan nilai V pada yang pertama persamaan yang diperolehi:

C = 2 ⋅ 10 = 20

Iaitu, ladang mempunyai dua puluh arnab.

- Masalah 3

Berapakah bilangan yang didarabkan oleh tujuh dan tolak enam memberikan dua puluh?

Jawapan

Jika kita memanggil nombor X yang tidak diketahui ini, ungkapan algebra ini boleh dibangkitkan:

Boleh melayani anda: Harta bersekutu: jumlah, pendaraban, contoh, latihan

7x - 6 = 29

Di sebelah kiri 6, ia melangkah ke sebelah kanan persamaan dengan tanda yang berubah:

7x = 29 + 6 = 35

Ia mengikuti bahawa x = 35/7 = 5

- Masalah 4

Dua kali ganda nombor 13 ditolak dan 7 adalah 7. Apa itu nombornya?

Jawapan

Jika kita memanggil nombor x itu, maka persamaan algebra adalah:

2 x - 13 = 7

Berapakah nilai 2x ?

Jawapannya ialah 2x mesti (13 + 7) supaya apabila anda mengeluarkan 13 ia adalah 7.

Ini bermakna bahawa 2x harus sama dengan 20, iaitu:

2x = 20

Nombor X yang didarab dengan 2 DA 20 adalah 10, oleh itu:

x = 10

- Masalah 5

Dua bilangan bulat berturut -turut menambah 23. Mencadangkan persamaan algebra yang membolehkan menentukan nombor dan mencarinya.

Jawapan

Katakan yang pertama dari nombor adalah n, jadi yang berikut adalah n+1 dan jumlah kedua -dua ini adalah n+(n+1). Ia juga diketahui bahawa jumlah jumlahnya adalah 23 maka persamaan ditulis:

n + (n + 1) = 23

Penyelesaiannya diperoleh terlebih dahulu memudahkan persamaan sebelah kiri:

2 n + 1 = 23

Kemudian 2 N dibersihkan oleh 1 kepada ahli yang betul dengan tanda yang diubah:

2 n = 23 - 1

Ahli yang betul diselesaikan:

2 n = 22

Seterusnya, n, lulus 2 yang mengadili anggota kiri yang membahagikan anggota kanan:

N = 22/2

Dan hasil akhir diperoleh:

N = 11

Rujukan

1. Baldor, a. Algebra. Editorial Kebudayaan Amerika Tengah c.Ke.
2. Carena, m. 2019. Manual Matematik PraUniversiti. Universiti Kebangsaan Pantai.
3. Cimanet. Ekspresi Algebra. Pulih dari: cinamet.UOC.Edu
4. Guzman ms. Ekspresi Algebra. Diperolehi daripada: konsep perlawanan.dari
5. Kuiz. Ekspresi Algebra. Pulih dari: mungkin.UPRM.Edu
6. Martha. Contoh ekspresi algebra. Pulih dari: superprof.adalah