Apakah nombor segi tiga? Sifat dan demonstrasi

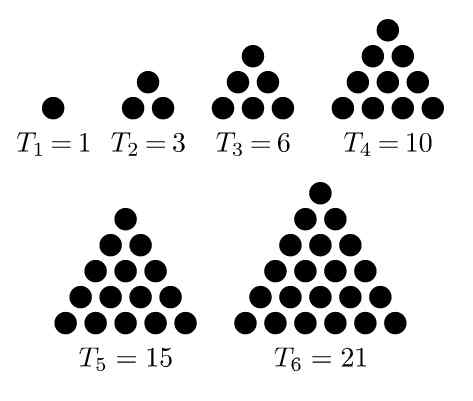
Ia dikenali sebagai nombor segi tiga ke urutan nombor yang diperoleh dengan membuat susunan atau angka titik segitiga sama rata. Yang pertama dari urutan adalah: 1, 3, 6, 10, 15, 21, ..

Isu segi tiga pertama adalah 1, yang kedua adalah 3, kerana ia diperolehi daripada menambah baris dua titik hingga yang sebelumnya, untuk membentuk segitiga sama rata dari tiga elemen.

Rajah 1. Urutan enam nombor segi tiga pertama. Sumber: Wikimedia Commons. Melchoir/cc by-sa (https: // creativeCommons.Org/lesen/by-sa/3.0)

Yang ketiga adalah 6, yang muncul ketika menambah baris tiga titik ke susunan sebelumnya, sehingga segitiga tiga titik dibentuk setiap sisi. 10 urutan diperolehi dengan menambahkan baris lain ke susunan sebelumnya supaya segitiga empat titik dibentuk setiap sisi.

Formula yang membolehkan anda mencari elemen n Dari urutan segi tiga, yang diketahui nombor segi tiga anterior adalah:

T_n = T_N-1 + n

Senarai enam nombor segi tiga pertama dicapai seperti ini:

-Pertama: 1

-Kedua: 1 + 2 = 3

-Ketiga: (1 +2) + 3 = 3 + 3 = 6

-Bilik: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Kelima: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Keenam: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

[TOC]

Sifat nombor segi tiga

1.- N-SIMO TN Triangular Nombor urutan nombor segi tiga adalah separuh daripada N didarab dengan N+1:

T_n = ½ n (n+1)

2.- Jumlah nombor segi tiga N-Ésimo dengan nombor segi tiga anterior, iaitu, (n-1) -sheimo, ia adalah persegi dinaikkan:

T_n + T_N-1= n²

3.- Perbezaan dalam nombor segi tiga n-ini kurang segitiga n-ésimo kurang satu adalah n:

T_n - T_N-1 = n

4.- Jumlah nombor segi tiga pertama dipanggil nombor tetrahedral SN dan sama dengan bahagian keenam produk yang didarab dengan (n + 1) dan didarabkan oleh (n + 2):

Boleh melayani anda: cukai

S_n= ⅙ n (n + 1) (n + 2)

5.- Setiap bilangan semula jadi n adalah hasil daripada jumlah tiga nombor segi tiga:

N = Δ1 + δ1 + δ3

Harta atau teorem terakhir ini ditemui oleh ahli matematik yang hebat Carl Friedrich Gauss pada tahun 1796, yang dia menjaringkan di dalam buku hariannya dengan meletakkan kekaguman Yunani Eureka! Apakah maksudnya "Saya telah mencapainya".

Itu adalah perkataan yang sama yang digunakan lebih awal oleh archimedes Yunani ketika dia menentukan berat badan yang tenggelam.

Dalam hubungan ini, nombor sifar diambil sebagai segi tiga dan mungkin ada pengulangan.

Demonstrasi

- Demonstrasi 1

Membuktikan bahawa nombor segi tiga n-Ini adalah:

T_n = ½ n (n+1)

Sangat mudah untuk menyimpulkan formula sebelumnya, jika kita menyedari bahawa kita boleh menambah bilangan mata yang sama kepada susunan segi tiga untuk membentuk segi empat titik mata.

Memandangkan jumlah titik susunan dalam bentuk segiempat adalah bilangan baris n didarab dengan bilangan lajur (N+1), Maka susunan segi tiga akan hanya mempunyai separuh dari titik susunan dalam bentuk segi empat.

Di sini digambarkan dalam Rajah 2.

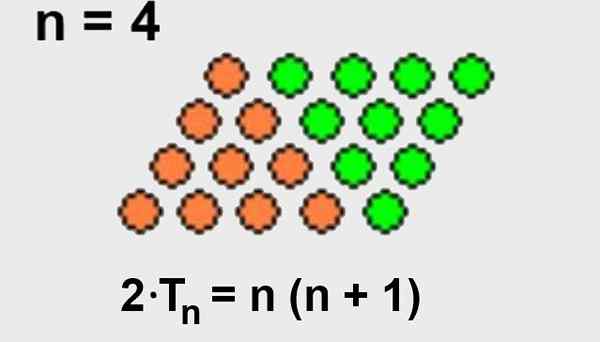Rajah 2. Pengaturan berbentuk persegi di mana jumlah mata adalah bilangan baris n didarab dengan bilangan lajur n+1. Jumlah mata juga dua kali ganda dari susunan segi tiga. Sumber: Wikimedia Commons.

- Demonstrasi 2

Menunjukkan bahawa jumlah n-Nombor segi tiga ini dengan n-Lebih kurang satu nombor segi tiga adalah n Squared:

T_n + T_N-1= n²

Telah ditunjukkan bahawa nombor segi tiga n-Ini diberikan oleh:

T_n= ½ n (n+1)

Oleh itu, nombor segi tiga anterior adalah:

T_N-1 = ½ (n-1) ((n-1) + 1) = ½ n (n-1)

Jumlah kedua -duanya kekal:

T_n + T_N-1 = ½ n (n + 1) + ½ n (n - 1)

½ n diambil untuk mendapatkan:

T_n + T_N-1 = ½ n [(n + 1) + (n - 1) = ½ n [n + 1 + n - 1]

Dan segera ungkapan dipermudahkan di dalam kurungan:

Ia dapat melayani anda: anggaran mengikut selang waktu

T_n + T_N-1 = ½ n [2 n] = ½ 2 n ⋅ n

Sekarang, ingat bahawa ½ untuk 2 adalah 1 dan bahawa n untuk n adalah N Square, anda mempunyai:

T_n + T_N-1 = n²

Harta ini juga boleh ditunjukkan secara geometrik, segitiga hanya selesai untuk membentuk persegi, seperti yang ditunjukkan dalam Rajah 3.

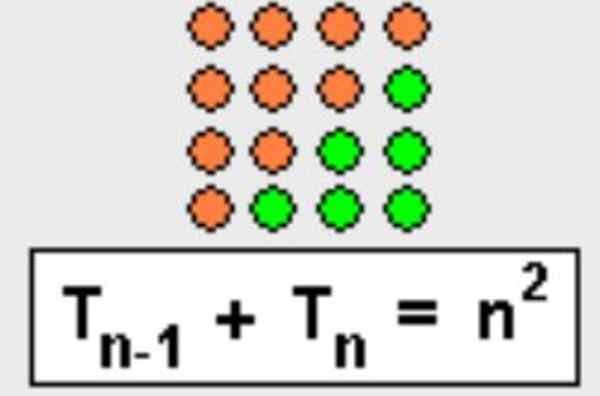Rajah 3. Jumlah nombor segi tiga N-ésimo dengan nombor segi tiga anterior sama dengan N Square. Sumber: Wikimedia Commons.

- Demonstrasi 3

Perbezaan dalam bilangan urutan segi tiga n tolak jumlah pesanan segitiga N-1 adalah n:

T_n - T_N-1 = n

Ini boleh diuji hanya dengan mengingati bahawa nombor segi tiga berikut diperoleh dari yang sebelumnya melalui formula:

T_n = T_N-1 + n

Dan dari situ jelas bahawa T_n - T_N-1 = n. Ia juga mudah untuk menggambarkannya secara grafik, seperti yang ditunjukkan dalam Rajah 4.

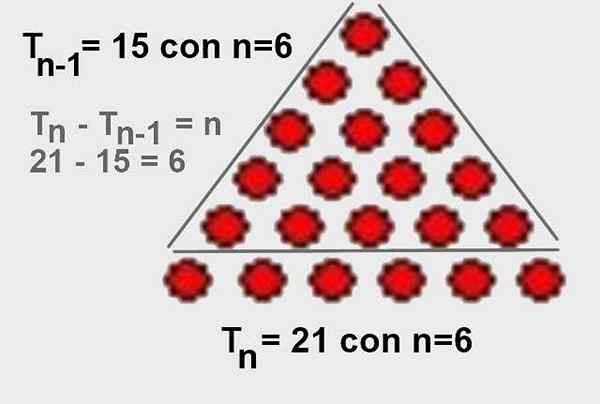Rajah 4. Perbezaan bilangan urutan segi tiga n kurang segitiga anterior pesanan n-1 adalah n. Sumber: Wikimedia Commons.

- Demonstrasi 5

Jumlah nombor N Triangular pertama sn Ia sama dengan bahagian keenam produk yang didarab dengan (n + 1) dan didarab dengan (n + 2):

S_n = ⅙ n (n + 1) (n + 2)

Mari kita gunakan bilangan segi tiga pesanan n: T_n= ½ n (n+1). Jumlah yang pertama n Nombor segi tiga akan menunjukkannya untuk S_n  

Sebagai contoh, S₁ bermaksud jumlah isu segi tiga pertama, yang pasti akan menjadi 1.

Kemudian mari kita lihat apakah formula yang kita cuba cuba dipatuhi dengan n = 1:

S₁ = ⅙ 1 ⋅2 ⋅3 = 1

Sesungguhnya, formula untuk n = 1 diperiksa. Sangat mudah untuk memvisualisasikan bahawa jumlah N+1 nombor segi tiga pertama akan menjadi jumlah pertama n lebih banyak nombor segi tiga seterusnya:

S_N+1 = S_n + T_N+1

Sekarang anggaplah formula S_n Ia dipenuhi untuk n, maka kami menggantikannya dalam ungkapan sebelumnya dan menambah bilangan urutan segi tiga N+1:

S_N+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]]

Boleh melayani anda: garis tegak lurus: ciri, contoh, latihan

Mari lihat langkah demi langkah apa yang diperoleh:

-Kami menjalankan jumlah dua ungkapan pecahan:

S_N+1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12 

-Ia dikeluarkan dari pengangka yang biasa hingga 2 (n + 1) (n + 2) dan memudahkan:

S_N+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Hasil sebelumnya bersetuju dengan formula Sn Jika n+1 diganti, yang telah ditunjukkan dengan induksi formula jumlah istilah segi tiga pertama.

Nombor tetrahedral

Hasil yang diperolehi dipanggil Bilangan pesanan tetrahedral n, Kerana ia seperti mengumpul lapisan segi tiga yang membentuk tetrahedron, seperti yang ditunjukkan dalam animasi berikut.

Rajah 5. Jumlah nombor segi tiga N sesuai dengan timbunan lapisan n, n-1, ..., 1 segitiga yang membentuk tetrahedron biasa. Sumber: Wikimedia Commons.

Rujukan

1. Camacho J. Penampilan nombor segi tiga yang tidak disangka. Pulih dari: Masscience.com
2. Claudio. Nombor segi tiga. Pulih dari: hanya nombor. Blogspot. com
3. Wikipedia. Nombor segi tiga. Pulih dari: Adakah.Wikipedia.com
4. Wikipedia. Nombor segi tiga. Diperoleh dari: dalam.Wikipedia.com
5. Wikipedia. Nombor tretrahedral. Diperoleh dari: dalam.Wikipedia.com