Apakah vektor coplanares? (Dengan latihan yang diselesaikan)

The Vektor Coplanares o Coplanarios adalah mereka yang terkandung di pesawat yang sama. Apabila anda hanya mempunyai dua vektor, ini selalu menjadi couplet.

Sekiranya anda mempunyai tiga atau lebih vektor, mungkin mana -mana daripada mereka tidak berada dalam satah yang sama dengan orang lain, oleh itu mereka tidak boleh dianggap Coplanares. Angka berikut menunjukkan satu set coplanar yang dilambangkan dalam vektor berani Ke, B, C dan D:

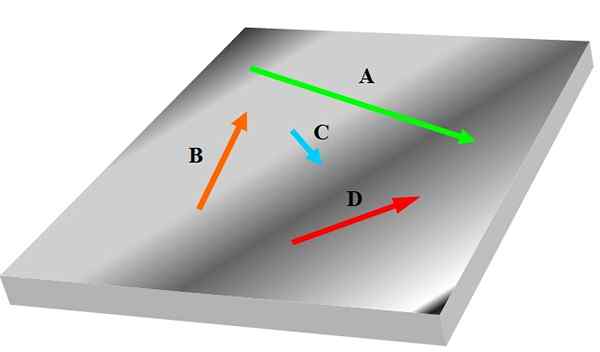Rajah 1. Empat Coplanares. Sumber: Diri Diri.

Vektor berkaitan dengan tingkah laku dan sifat magnitud fizikal yang relevan dalam sains dan kejuruteraan; contohnya kelajuan, pecutan dan kekuatan.

Daya menghasilkan kesan yang berbeza pada objek apabila cara ia digunakan diubah, contohnya mengubah intensiti, arah dan makna. Masih mengubah salah satu parameter ini hasilnya jauh berbeza.

Dalam banyak aplikasi, baik dalam statik dan dinamik, daya yang bertindak pada badan berada di pesawat yang sama, oleh itu mereka dianggap coplanares.

[TOC]

Syarat untuk vektor menjadi coplanares

Untuk tiga vektor menjadi coplanar, mereka mesti berada di pesawat yang sama dan ini berlaku jika mereka memenuhi mana -mana syarat berikut:

-Vektor selari, oleh itu komponen mereka berkadar dan bergantung secara linear.

-Produk campuran anda tidak sah.

-Sekiranya anda mempunyai tiga vektor dan mana -mana daripada mereka boleh ditulis sebagai gabungan linear dari dua yang lain, vektor ini adalah coplanares. Contohnya vektor yang dihasilkan dari jumlah dua orang lain, ketiga -tiga mereka berada dalam pesawat yang sama.

Boleh melayani anda: voltmeter: ciri, operasi, apa itu, jenis

Sebagai alternatif, keadaan coplanarity dapat diwujudkan seperti berikut:

U v w Mereka adalah coplanares jika terdapat tiga nombor (skalar) α, β, γ sehingga αatau + βv + γW = 0 Dengan (α, β, γ) berbeza dari (0, 0, 0)

Produk bercampur antara tiga vektor

Produk campuran antara vektor ditakrifkan dengan tiga vektor atau, v dan W, mengakibatkan skalar yang hasil daripada melakukan operasi berikut:

atau · (v x W) = atau · (v x W)

Pertama produk silang yang ada dalam kurungan dibuat: v x W, yang hasilnya adalah vektor normal (tegak lurus) ke satah di mana mereka begitu v sebagai W.

Yeah atau berada di satah yang sama seperti v dan W, Secara semulajadi produk skalar (produk titik) antara u dan vektor biasa mestilah 0. Dengan cara ini disahkan bahawa ketiga -tiga vektor adalah coplanares (mereka terletak di atas kapal terbang yang sama).

Apabila produk bercampur tidak batal, hasilnya sama dengan jumlah parallelepiped yang mempunyai vektor atau, v dan W sebagai sisi bersebelahan.

Aplikasi

Pasukan coplanares, serentak dan bukan kolineal

Kekuatan serentak Semuanya digunakan pada titik yang sama. Sekiranya mereka juga coplanar, mereka boleh digantikan dengan hanya satu, yang dipanggil mengakibatkan daya Dan ia mempunyai kesan yang sama seperti kuasa asal.

Sekiranya badan berada dalam keseimbangan terima kasih kepada tiga pasukan coplanares, serentak dan tidak -kolineal (bukan parallel), yang dipanggil Ke, B dan C, Dia Teorem Lamy Beliau menegaskan bahawa hubungan antara kuasa -kuasa ini (magnitud) adalah seperti berikut:

A / SIN α = B / SEN β = C / SEN γ

Dengan α, β dan γ sebagai sudut yang menentang daya yang digunakan, seperti yang ditunjukkan dalam angka berikut:

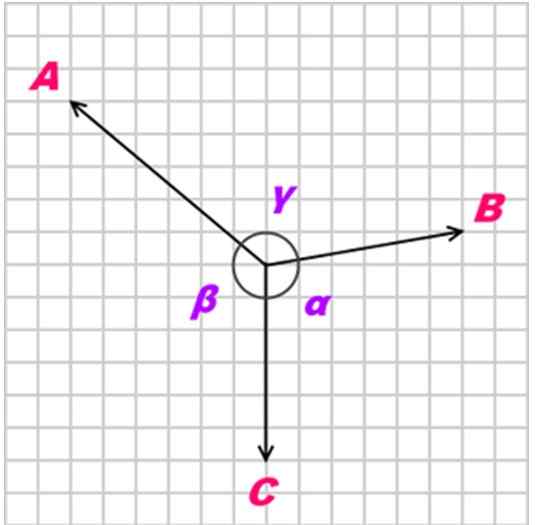Rajah 2. Tiga pasukan A, B dan C Coplanares bertindak pada objek. Sumber: Kiwakwok di Bahasa Inggeris Wikipedia [Domain Awam]

Latihan yang diselesaikan

-Latihan 1

Cari nilai k supaya vektor berikut adalah coplanares:

Boleh melayani anda: mesin Carnot

atau =

v =

W =

Penyelesaian

Oleh kerana komponen vektor ada, kriteria produk campuran digunakan, oleh itu:

atau · (v x W) = 0

Ia diselesaikan terlebih dahulu v x W. Vektor akan dinyatakan dari segi vektor unit Yo, J dan k yang membezakan tiga arah tegak lurus di ruang angkasa (lebar, tinggi dan mendalam):

v= 4 Yo + J + 0 k

W= -1 Yo + 2J -1 k

v x W = -4 (i x i) + 8 (i x j) - 4 (i x k) - (J x i) + 2 (J x j) - 2 (J x k) = 8 k + 4 J + k -2 i = -2 Yo + 4 J + 9 k

Produk skalar kini dicadangkan antara u dan vektor yang mempunyai hasil dari operasi sebelumnya, operasi yang sepadan hingga 0:

atau · (v x W) = (-3 Yo + k J + 2 k) · (-2 Yo + 4 J + 9 k) = 6 + 4k +18 = 0

24 + 4k = 0

Nilai yang dicari ialah: k = - 6

Jadi vektor atau adalah:

atau =

-Senaman 2

Angka ini menunjukkan objek yang beratnya W = 600 N, tergantung seimbang terima kasih kepada kabel yang diletakkan mengikut sudut yang ditunjukkan dalam Rajah 3. Adakah mungkin untuk menggunakan teorem Lamy dalam keadaan ini? Dalam apa jua keadaan mencari magnitud T₁, T₂ dan T₃ yang menjadikan keseimbangan mungkin.

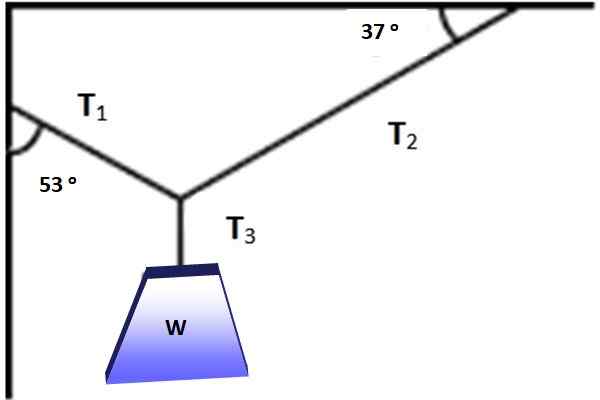Rajah 3. Berat badan tergantung dalam keseimbangan di bawah tindakan tiga ketegangan yang ditunjukkan. Sumber: Diri Diri.

Penyelesaian

Teorem Lamy boleh digunakan dalam keadaan ini jika simpulan di mana ketegangan ketiga -tiga digunakan dipertimbangkan, kerana ia membentuk sistem pasukan Coplanar. Pertama gambarajah badan percuma dibuat untuk berat loket, untuk menentukan magnitud t_3:

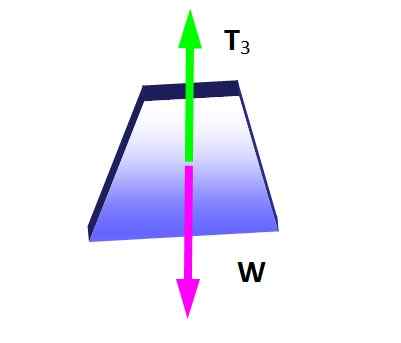Rajah 4. Rajah badan percuma untuk berat badan yang tergantung. Sumber: Diri Diri.

Dari keadaan keseimbangan ia mengikutinya:

Boleh melayani anda: Pembelahan bunyi: Apa, contoh, aplikasi

T₃  = W = 600 n

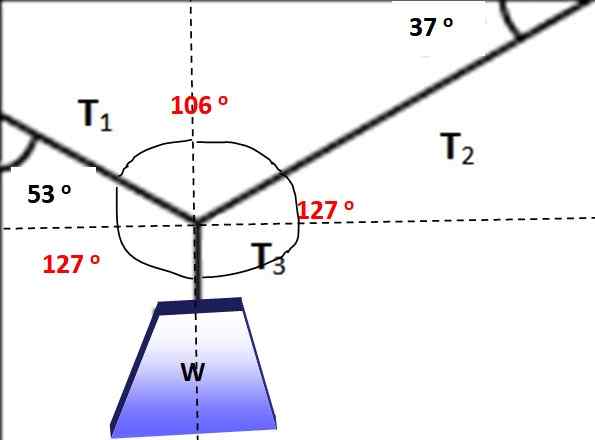
Sudut antara daya ditandakan dengan warna merah dalam angka berikut, ia dapat dengan mudah disahkan bahawa jumlahnya adalah 360 °. Ia kini mungkin untuk memohon teorem Lamy, kerana salah satu kuasa dan tiga sudut di antara mereka diketahui:

Rajah 5.- Red sudut untuk memohon teorem Lamy. Sumber: Diri Diri.

T₁ / Sen 127º = w / sen 106º

Oleh itu: t₁ = sen 127º (w /sen 106º) = 498.5 n

Sekali lagi teorem Lamy digunakan untuk membersihkan t₂:

T₂ / dosa 127 = t₁ / Sen 127º

T₂ = T₁ = 498.5 n

Rujukan

1. Figueroa, d. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. 31-68.
2. Fizikal. Modul 8: vektor. Pulih dari: frtl.Utn.Edu.ar
3. Hibbeler, R. 2006. Mekanik untuk jurutera. Statik. Edisi ke -6. Syarikat Editorial Continental.28-66.
4. McLean, w. Siri Schaum. Mekanik untuk Jurutera: Statik dan Dinamik. Edisi ke -3. McGraw Hill. 1-15.
5. Wikipedia. Vektor. Pulih dari: ia adalah.Wikipedia.org.