Definisi dan formula purata kelajuan sudut, latihan yang diselesaikan

The Purata halaju sudut putaran ditakrifkan sebagai sudut yang diputar oleh kedudukan unit masa vektor titik yang menggambarkan pergerakan bulat. Bilah kipas siling (seperti yang ditunjukkan dalam Rajah 1), ikut pergerakan bulat dan kelajuan putaran sudut purata dikira dengan mengambil nisbah antara sudut yang berpaling dan masa di mana sudut itu dilalui.

Peraturan yang diikuti oleh pergerakan putaran adalah dengan cara tertentu yang serupa dengan saudara -saudara pergerakan translasi yang sudah. Jarak yang dilalui juga boleh diukur dalam meter, namun magnitud sudut mengambil kaitan khas kerana mereka sangat memudahkan perihalan pergerakan itu.

Rajah 1. Bilah kipas mempunyai halaju sudut. Sumber: Pixabay

Huruf Yunani biasanya digunakan untuk magnitud sudut dan huruf Latin untuk magnitud linear yang sepadan.

[TOC]

Definisi dan formula

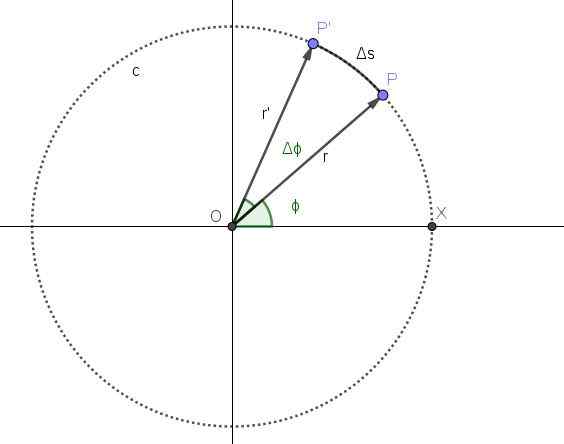
Rajah 2 mewakili pergerakan titik pada trajektori bulat c. Kedudukan p dari titik sepadan dengan t -segera t dan kedudukan sudut yang sepadan dengan saat itu adalah φ. 

Dari saat suatu tempoh masa berlalu ΔT. Dalam tempoh itu kedudukan baru titik adalah p 'dan kedudukan sudut telah meningkatkan sudut δφ.

Rajah 2. Pergerakan bulat satu titik. Sumber: Diri Diri

Halaju sudut purata Ω adalah sudut yang mengembara per unit masa, supaya imba δφ/Δt akan mewakili halaju sudut purata antara momen t dan t+Δt:

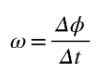
Oleh kerana sudut diukur dalam radian dan masa dalam beberapa saat, perpaduan halaju sudut purata adalah rad/s. Sekiranya anda ingin mengira halaju sudut Hanya pada masa t, maka kuota Δφ/Δt perlu dikira apabila Δt ➡0.

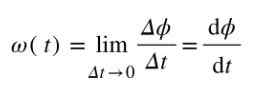Unit ukuran halaju sudut segera juga rad/s.

Boleh melayani anda: 31 jenis daya dalam fizik dan ciri mereka

Putaran seragam

Pergerakan putaran adalah seragam jika pada bila -bila masa diperhatikan, sudut yang dilalui adalah sama dalam tempoh yang sama. Sekiranya putaran seragam, maka halaju sudut pada bila -bila masa bertepatan dengan halaju sudut purata.

Dalam pergerakan putaran seragam, masa di mana giliran lengkap dipanggil dipanggil tempoh Dan ia dilambangkan dengan t. 

Di samping itu, apabila sudut perjalanan penuh, ia adalah 2π, jadi dalam putaran seragam halaju sudut Ω berkaitan dengan tempoh t, dengan formula berikut:

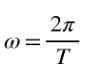
The kekerapan F putaran seragam seperti nisbah antara bilangan giliran dan masa yang dihabiskan untuk mengembara mereka, iaitu, pada masa itu ΔT ada kekerapannya:

F = n/Δt

Sebagai pangkuan (n = 1) ia dilalui dalam masa t (tempoh), hubungan berikut boleh didapati:

F = 1/t

Iaitu, dalam putaran seragam halaju sudut berkaitan dengan kekerapan melalui hubungan:

Ω = 2π ・ f

Hubungan antara kelajuan sudut dan kelajuan linear

Kelajuan linear v, Ia adalah kuota antara jarak perjalanan dan tempoh masa yang digunakan untuk mengembara. Dalam Rajah 2 jarak perjalanan adalah panjang arka ΔS. 

Arka ΔS adalah berkadar dengan sudut yang mengembara Δφ dan radio r, memenuhi hubungan berikut:

ΔS = r ・ δφ

Bila -bila masa Δφ diukur dalam radian.

Jika kita membahagikan ungkapan sebelumnya antara tempoh masa Δt kita akan memperoleh:

(ΔS/ΔT) = R ・ (Δφ/ΔT)

Nisbah ahli pertama adalah kelajuan linear dan kota ahli kedua halaju sudut purata:

Boleh melayani anda: Gunung Olympus (Marikh)

v = r ・ Ω

Latihan yang diselesaikan

-Latihan 1

Petua bilah kipas bumbung yang ditunjukkan dalam Rajah 1 bergerak dengan kelajuan 5 m/s dan bilah adalah 40 cm radius.

Dengan data ini hitung: i) halaju sudut purata roda, ii) bilangan giliran yang diberikan roda dalam kedua, iii) tempoh dalam beberapa saat.

Penyelesaian 

i) Kelajuan linear ialah v = 5 m/s.

Radio adalah r = 0.40 m.

Dari hubungan antara kelajuan linear dan kelajuan sudut kita membersihkan yang terakhir:

v = r ・ ω => ω = v/r = (5 m/s)/(0.40 m) = 12.57 rad/s

ii) Ω = 2π ・ f => f = ω / 2π = (12.57 rad / s) / (2π rad) = 2 giliran / s

iii) t = 1 / f = 1 / (2 giliran / s) = 0.5 s setiap pangkuan.

-Latihan 2

Berjalan -jalan mainan bergerak di trek bulat radius 2m. Pada 0S kedudukan sudutnya adalah 0 rad, tetapi selepas masa t kedudukan sudutnya adalah

φ (t) = 2 ・ t .

Dengan data ini 

i) Kirakan halaju sudut purata dalam selang masa berikut [0s, 0.5s]; [0.5s, 1.0s]; [1.0, 1.5s] dan akhirnya dalam tempoh [0.0, 1.5s]. 

ii) Berdasarkan hasil Bahagian I) apa yang dapat dikatakan mengenai pergerakan itu?

iii) Tentukan kelajuan linear purata dalam tempoh masa yang sama bahagian i)

iv) Cari kelajuan sudut dan kelajuan linear untuk bila -bila masa.

Penyelesaian 

i) Halaju sudut purata diberikan oleh formula berikut:

Kami meneruskan untuk mengira sudut yang dilalui dan tempoh masa berlalu dalam setiap selang waktu.

Interval 1: δφ = φ (0.5s) - φ (0.0s) = 2 (rad/s)*0.5s - 2 (rad/s)*0.0s = 1.0 rad

                   Δt = 0.5s - 0.0s = 0.5s

Boleh melayani anda: BTU (Unit Thermal): Kesamaan, Kegunaan, Contoh

                   Ω = Δφ/Δt = 1.0rad/0.5s = 2.0 rad/s

Selang 2: Δφ = φ (1.0s) - φ (0.5s) = 2 (rad/s)*1.0s - 2 (rad/s)*0.5s = 1.0 rad

                   Δt = 1.0s - 0.5s = 0.5s

                   Ω = Δφ/Δt = 1.0rad/0.5s = 2.0 rad/s

Interval 3: δφ = φ (1.5s) - φ (1.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*1.0s = 1.0 rad

                   Δt = 1.5s - 1.0s = 0.5s

                   Ω = Δφ/Δt = 1.0rad/0.5s = 2.0 rad/s

Interval 4: δφ = φ (1.5s) - φ (0.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*0.0s = 3.0 rad

                   Δt = 1.5s - 0.0s = 1.5s

                   Ω = Δφ/Δt = 3.0rad/1.5s = 2.0 rad/s

ii) Memandangkan hasil sebelumnya, di mana halaju sudut purata dikira dalam selang waktu yang berlainan, hasil yang sama selalu diperolehi. Nampaknya menunjukkan bahawa ia adalah gerakan pekeliling seragam. Walau bagaimanapun, keputusan ini tidak muktamad.

Cara untuk memastikan kesimpulannya adalah untuk mengira halaju sudut purata untuk selang sewenang -wenangnya [t, t -t)

                                     Δt = t ' - t

                                     Ω = Δφ/Δt = 2*(t'-t)/(t'-t) = 2.0 rad/s

Ini bermaksud bahawa berjalan -jalan mainan mempunyai kelajuan sudut purata yang berterusan sebanyak 2 rad/s dalam mana -mana tempoh masa yang dipertimbangkan. Tetapi anda boleh pergi lebih jauh jika halaju sudut segera dikira:

Ini ditafsirkan sebagai kereta mainan pada setiap masa mempunyai kelajuan sudut tetap = 2 rad/s.

Rujukan

1. Giancoli, d. Fizik. Prinsip dengan aplikasi. Edisi ke -6. Prentice Hall. 30-45.
2. Kirkpatrick, l. 2007. Fizik: Lihatlah dunia. 6^TA Edisi Singkat. Pembelajaran Cengage. 117.
3. Resnick, r. (1999). Fizikal. Jilid 1. Edisi ketiga dalam bahasa Sepanyol. Mexico. Syarikat Editorial Continental s.Ke. daripada c.V. 33-52.
4. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Edisi. Mexico. Editor Pembelajaran Cengage. 32-55.
5. Wikipedia. Halaju sudut. Pulih dari: wikipedia.com