Akar persegi 3 (penyelesaian dan penjelasan yang mudah)

Akar persegi 3 ialah 1.73205080756887.

Ia boleh dinyatakan:

√3 = 1.73205080756887

Untuk mengetahui apa itu 3 akar persegi, Penting untuk mengetahui definisi akar kuadrat dari nombor. Memandangkan nombor positif "a", akar kuadrat "a", yang dilambangkan oleh √a, adalah nombor positif "b" sehingga apabila "b" didarabkan olehnya, hasilnya adalah "a".

Definisi matematik mengatakan: √a = b ya, dan hanya jika, b² = b*b = a. Oleh itu, untuk mengetahui apakah akar kuadrat 3, iaitu, nilai √3, nombor "b" mesti dijumpai bahawa b² = b*b = √3.

Di samping itu, √3 adalah nombor yang tidak rasional, yang terdiri daripada jumlah perpuluhan yang tidak terhingga. Atas sebab ini, sukar untuk mengira akar kuadrat 3 secara manual.

3 akar persegi

Sekiranya kalkulator digunakan, dapat dilihat bahawa akar kuadrat 3 adalah 1.73205080756887 ..

Sekarang, anda boleh cuba untuk menghampiri nombor ini secara manual seperti berikut:

-1*1 = 1 dan 2*2 = 4, ini mengatakan bahawa akar kuadrat 3 adalah nombor antara 1 dan 2.

-1.7*1.7 = 2.89 dan 1.8*1.8 = 3.24, oleh itu, angka perpuluhan pertama ialah 7.

-1.73*1.73 = 2.99 dan 1.74*1.74 = 3.02, oleh itu angka perpuluhan kedua ialah 3.

-1,732*1,732 = 2.99 dan 1,733*1,733 = 3,003, oleh itu, angka perpuluhan ketiga ialah 2.

Dan sebagainya anda boleh meneruskan. Ini adalah cara manual untuk mengira akar kuadrat 3.

Terdapat juga teknik lain yang lebih maju, seperti kaedah Newton-Raphson, yang merupakan kaedah berangka untuk mengira anggaran.

Di mana kita dapat mencari nombor √3?

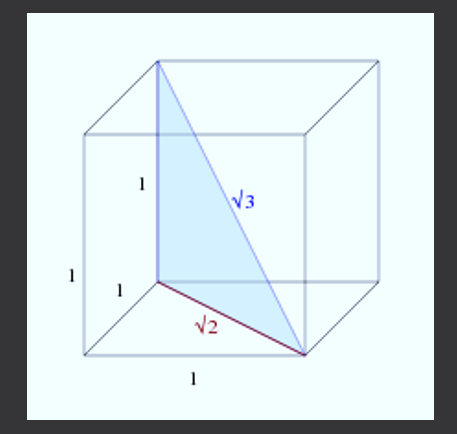
Oleh kerana nombor rumit, ia boleh dianggap bahawa ia tidak muncul dalam objek sehari -hari tetapi ini palsu. Sekiranya anda mempunyai kiub (kotak persegi), sehingga panjang sisinya adalah 1, maka pepenjuru kiub akan mempunyai ukuran √3.

Untuk mengesahkan ini, teorem Pythagoras digunakan yang mengatakan: Beri.

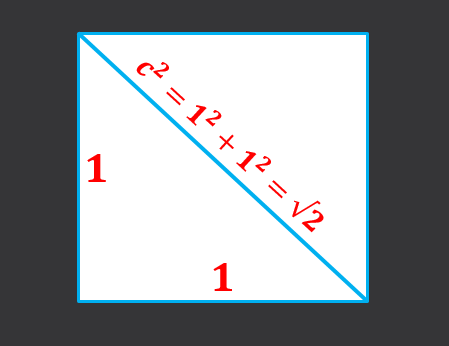
Mempunyai sisi sisi 1, anda perlu pepenjuru segi empat pangkalannya adalah sama dengan jumlah kuadrat kategori, iaitu, C² = 1²+1² = 2, oleh itu, pepenjuru dasar √2.

Sekarang, untuk mengira pepenjuru kiub, anda dapat melihat angka berikut.

Segitiga segi empat tepat baru mempunyai kaki panjang 1 dan √2, oleh itu, apabila menggunakan teorem pythagoras untuk mengira panjang pepenjuru yang diperolehi: c² = 1 ²+(√2) ² = 1+2 = 3, dikatakan , C = √3.

Oleh itu, panjang pepenjuru baldi sisi 1 adalah sama dengan √3.

√3 nombor yang tidak rasional

Pada mulanya dikatakan bahawa √3 adalah nombor yang tidak rasional. Untuk mengesahkan ini, ia diasumsikan oleh ketidaksuburan yang merupakan nombor rasional, yang terdapat dua nombor "A" dan "B", sepupu relatif, seperti A/B = √3.

Apabila kesamaan terakhir dan jelas "a²", persamaan berikut diperolehi: a² = 3*b². Ini mengatakan bahawa "a²" adalah pelbagai 3, yang menyimpulkan bahawa "a" adalah pelbagai 3.

Menjadi "" berganda 3, ada integer "k" seperti a = 3*k. Oleh itu, dengan menggantikan persamaan kedua ia diperolehi: (3*k) ² = 9*k² = 3*b², yang sama dengan b² = 3*k².

Seperti dahulu, kesamaan terakhir ini membawa kepada kesimpulan bahawa "B" adalah pelbagai 3.

Kesimpulannya, "A" dan "B" adalah kedua -dua gandaan 3, yang merupakan percanggahan, kerana pada mulanya ia diandaikan bahawa mereka adalah sepupu relatif.

Oleh itu, √3 adalah nombor yang tidak rasional.