Sebab Trigonometrik Contoh, Latihan dan Aplikasi

The Alasan trigonometri Mereka adalah kuota atau alasan yang boleh dilakukan dengan nilai sisi segitiga yang betul. Sisi ini adalah: dua kategori yang membentuk 90º antara satu sama lain dan hipotenus, yang membentuk sudut akut θ dengan salah satu kategori.

6 quotients boleh dibentuk. Nama mereka dan singkatan masing -masing adalah:

• Brease (Sen)
• Coseno (cos)
• Tangent (TG atau TAN)
• Cotangent (CTG atau Cotan)
• Secante (sec) dan
• Harvester (keharmonian)

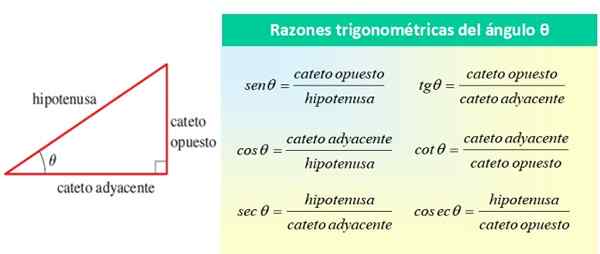
Kesemua mereka merujuk kepada sudut θ, seperti yang ditunjukkan dalam angka berikut:

Rajah 1. Sebab trigonometri sudut akut θ. Sumber: f. Zapata.

Sebab -sebab trigonometri asas sudut θ adalah sin θ, cos θ dan tan θ, sementara sebab -sebab yang selebihnya dapat dinyatakan dari segi tiga. Dari gambar sebelumnya, anda dapat melihatnya:

• Sec θ = 1/ cos θ
• bahaya θ = 1/ sin θ
• Cot θ = 1/Tg θ

Saiz sisi segitiga tidak mempengaruhi nilai sebab -sebabnya, kerana dua segitiga yang sudutnya mengukur sama dengan segitiga yang sama dan sebutan masing -masing di antara sisi mempunyai nilai yang sama.

[TOC]

Contoh

Sebagai contoh, mari kita mengira sebab -sebab trigonometri sudut θ dalam segitiga berikut:

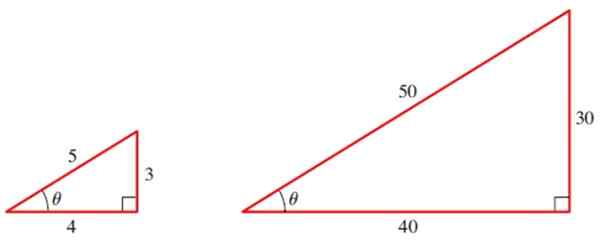Rajah 2. Dua segitiga yang serupa mempunyai alasan trigonometri yang sama dari sudut mereka. Sumber: Stewart, J.Preccculment: Matematik untuk Pengiraan.

Untuk segitiga kecil kita mempunyai tiga sebab asas sudut θ:

dosa θ = 3/5

cos θ = 4/5

Tg θ = ¾

Dan sekarang mari kita mengira tiga sebab asas θ dengan segitiga besar:

sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

Tg θ = 30/40 = ¾

Perincian penting yang perlu dipertimbangkan adalah seperti berikut: kedua -dua dosa θ dan cos θ kurang dari 1, kerana kategori selalu mengukur kurang daripada hipotenus. Malah:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Latihan yang diselesaikan

Dalam latihan berikut, diminta untuk menyelesaikan segitiga yang betul, yang bermaksud mencari panjang tiga sisi dan ukuran sudut dalamannya, salah satunya selalu mengukur 90º.

Boleh melayani anda: Persamaan Pertama -Degree: Formula, Cara Menyelesaikannya, Contoh, Latihan

Teorem Pythagoras digunakan untuk segitiga segi empat tepat dan sangat berguna apabila dua sisi diketahui dan yang hilang mesti ditentukan. Teorem berkata:

Hypotenuse² = bertentangan Cateto² + Cateto bersebelahan²

Kita dapat mengesahkan teorem pythagoras dengan segitiga kecil Rajah 2, yang kakinya 3 dan 4. Perintah di mana kategori diambil tidak penting. Memohon teorem yang kita ada:

Hypotenuse² = 3² + 4² = 9 + 16 = 25

Oleh itu hipotenus adalah:

Hypotenuse = √25 = 5

- Latihan 1

Kirakan sebab -sebab trigonometri sudut yang ditunjukkan dalam segitiga berikut:

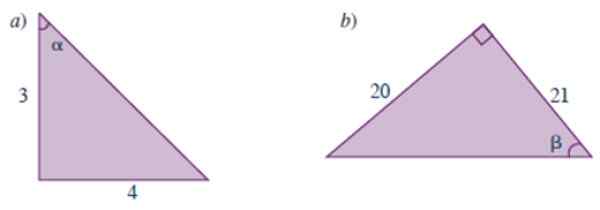Rajah 3.- Segitiga untuk tahun diselesaikan 1. Sumber: Carena, m. 2019. Manual Matematik PraUniversiti.

Penyelesaian kepada

Segitiga ini adalah sama dalam Rajah 3, tetapi mereka meminta kami atas sebab -sebab trigonometri sudut akut yang lain, dilambangkan α. Kenyataan itu tidak menawarkan nilai hipotenusa, bagaimanapun, dengan menggunakan teorem pythagoras kita tahu bahawa ia bernilai 5.

Sebab -sebabnya dapat dikira secara langsung dari definisi, berhati -hati ketika memilih kaki yang bertentangan dengan sudut α untuk mengira SEN α. Mari kita lihat:

• dosa α = 4/5
• cos α = 3/5
• TG α = 4/3
• Cot α = ¾
• Sec α = 1/(3/5) = 5/3
• bahaya α = 1/(4/5) = 5/4

Dan seperti yang dapat kita lihat, nilai -nilai sebab trigonometri telah ditukar. Sesungguhnya, α dan θ adalah sudut pelengkap, yang bermaksud bahawa mereka menambah 90º. Dalam kes ini, ia dipenuhi bahawa sen α = cos θ dan sebagainya atas sebab -sebab lain.

Penyelesaian b

Mari kita mengira hipotenus segitiga melalui teorem Pythagoras:

Hypotenuse² = 20² + dua puluh satu² = 841

√841 = 29

Kemudian 6 sebab trigonometri sudut β adalah:

• Sen β = 20/29
• cos β = 21/29
• TG β = 20/21
• COT β = 21/20
• SEC β = 1/(21/29) = 29/21
• bahaya β = 1/(20/29) = 20/29

Boleh melayani anda: Operasi gabungan

- Latihan 2

a) Cari nilai x dalam angka.

b) Kirakan perimeter 3 segi tiga yang ditunjukkan.

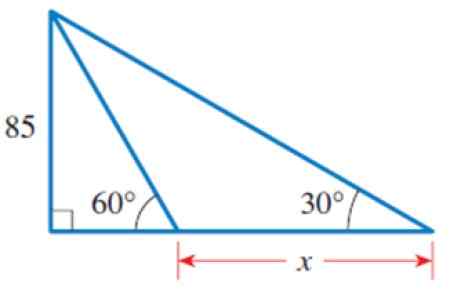Rajah 4. Segitiga untuk tahun diselesaikan 2. Sumber: Stewart, J. Preccculment: Matematik untuk Pengiraan.

Penyelesaian kepada

Dalam angka ini kita dapat mengenal pasti beberapa segitiga, khususnya segitiga segi empat tepat di sebelah kiri, yang mempunyai kategori yang sama dengan 85 dan sudut akut 60º.

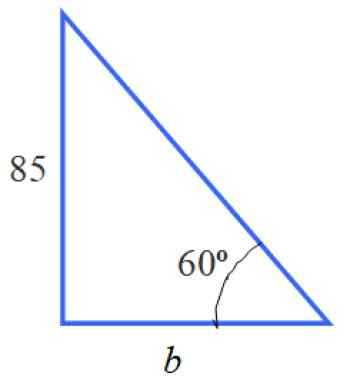Rajah 5. Segitiga di sebelah kiri.

Dengan maklumat segitiga ini kita dapat mengira sisi b. Bukan ukuran pernyataan itu, tetapi mengetahui nilainya adalah langkah sebelumnya.

Untuk menentukan sebab yang sesuai ialah Tg 60 º = 85 /B, kerana B adalah kaki bersebelahan dengan 60 ° dan 85 adalah sebaliknya dengan sudut tersebut. Oleh itu:

B = 85 / Tg 60º = 85 / √3

Setelah dikenali B, kami akan menggunakan segitiga segi empat tepat yang besar dan luar, yang mempunyai sisi yang sama dengan segitiga sebelumnya: yang berukuran 85. Ini adalah cateto yang menentang sudut 30º.

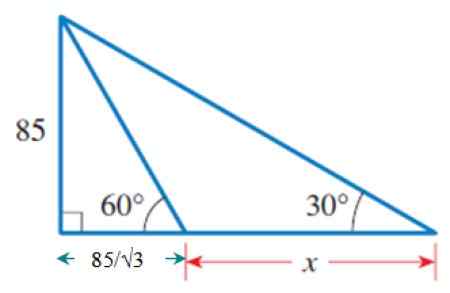Rajah 6. Segitiga luar, di mana sebahagian daripada pangkalan sudah diketahui.

Situ:

Cateto bersebelahan dengan 30º = (85/√3) + x

Sekarang kita dapat menaikkan perkara berikut:

85 / [(85 / √3) + x] = Tg 30º

Apa yang ada dalam kurungan persegi melipatgandakan 30º TG:

85 = [(85/√3) + x]. TG 30º

Memohon harta pengedaran pendaraban:

85 = TG 30º. (85/√3) + x. TG 30º

Oleh itu:

x.TG 30º = 85 - TG 30º. (85/√3) = 85 [1 - Tg 30º . (1/√3)] = 85 . (2/3) = 170/3

Menggantikan nilai TG 30º = √3/3:

x = (170/3) ÷ (√3 / 3) = 98.lima belas

Penyelesaian b

Perimeter segitiga kecil

H₁ Hypotenuse segitiga ini, yang boleh dikira oleh teorem Pythagoras atau melalui alasan trigonometri, contohnya cos 60º:

cos 60 º = 85 / √3 / h₁→ h₁ = (85/√3) ÷ cos 60º = 98.1

Untuk mencari p, perimeter segitiga ini, kami hanya menambah 3 sisi:

Boleh melayani anda: Statistik deskriptif: sejarah, ciri, contoh, konsep

P = 85 + (85/√3) + 98.1 = 232.2

Perimeter segitiga luaran

H₂ kepada hipotenus segitiga luaran:

Sen 30º = 85 ÷ h₂  

h₂ = 85 ÷ dosa 30º = 170

Untuk segitiga ini perimeter adalah:

P = 85 + [(85/√3) + 98.15] + 170 = 402.22

Perimeter segi tiga bukan

Dari segi tiga ini kita sudah tahu semua sisi:

P = x + h₁ + h₂ = 98.15 + 98.15 + 170 = 366.3

Aplikasi alasan trigonometri

Sebab trigonometri mempunyai banyak aplikasi praktikal, contohnya ketinggian dapat dikira.

Katakan menara air adalah 325 kaki dari bangunan. Observer yang terletak di dalam tetingkap nota bahawa sudut ketinggian hujung atas menara adalah 39 º, manakala sudut kemurungan yang mana asas menara dilihat adalah 25º. Keajaiban:

a) Berapakah ketinggian menara?

b) berapa tingkap?

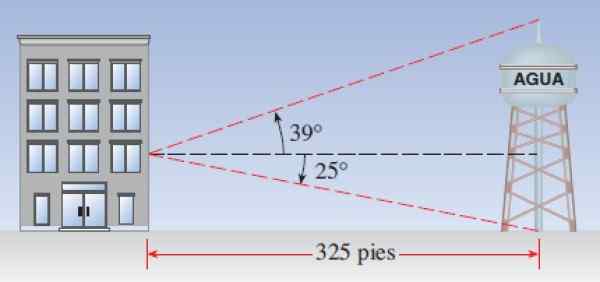Rajah 7. Skim untuk mengira ketinggian vista torre dari bangunan. Sumber: Stewart, J. Preccculment: Matematik untuk Pengiraan.

Penyelesaian kepada

Dari Cateto yang bertentangan dengan 39 segitiga atas kita mendapat sebahagian daripada jawapannya:

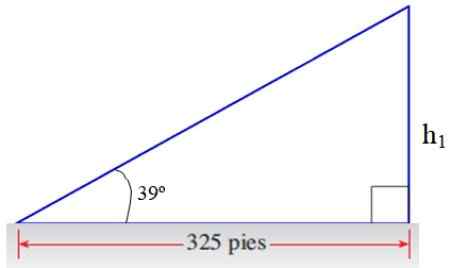Rajah 8. Segitiga untuk Latihan Aplikasi. Sumber: f. Zapata.

h₁/325 = Tg 39º → H₁ = 325 . TG 39º kaki = 263.2 kaki

Dengan cara yang sama, kita mendapat selebihnya ketinggian menara, yang dipanggil H₂ Dari segitiga bawah:

h₂/325 = Tg 25º → H₂ = 325 . TG 25º kaki = 151.6 kaki

Ketinggian jumlah menara adalah h₁ + h₂ = 263.2 + 151.6 kaki = 414.7 kaki.

Penyelesaian b

Tetingkap tepat pada ketinggian h₂ tanah:

h₂ = 151.6 kaki.

Rujukan

1. Carena, m. 2019. Manual Matematik PraUniversiti. Universiti Kebangsaan Pantai.
2. Hoffman, J. Pemilihan masalah matematik. Jilid 3.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.