Kawasan pentagon biasa dan tidak teratur bagaimana ia diambil, latihan

Untuk mengira kawasan pentagon Pertama kita perlu menentukan sama ada ini biasa atau tidak. Pentagon adalah poligon, angka rata tertutup lima sisi. Apabila poligon biasa, ini bermakna bahawa panjang sisinya adalah sama dan sudut dalamannya juga.

Dalam hal ini, terdapat formula untuk mengira kawasan tepat poligon biasa, mengetahui beberapa ciri utamanya, yang akan kami cakap kemudian.

Dua pentagon

Sekiranya poligon tidak biasa, iaitu, ia mempunyai saiz yang berbeza, dan sudut dalaman yang tidak sama rata, tidak ada formula tunggal.

Walau bagaimanapun, ahli matematik telah menemui strategi pengiraan, seperti membahagikan angka kepada orang lain dengan jumlah yang paling rendah, seperti segitiga, dataran dan segi empat tepat, yang dimensinya diketahui atau mudah dikira.

Satu lagi prosedur untuk mengira bidang poligon secara umum, mengetahui koordinat simpangnya, adalah kaedah yang dipanggil Penentu Gauss, bahawa kita akan menerangkan kemudian.

[TOC]

Cara mengira kawasan pentagon biasa?

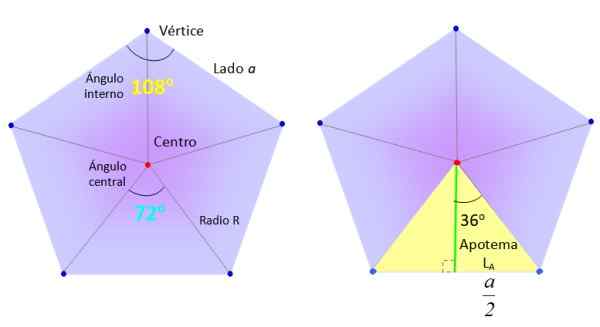
Kami akan mengambil pentagon biasa dari sisi A, dan kami akan membahagikannya menjadi 5 segitiga yang sama seperti yang ditunjukkan dalam angka, melukis segmen dari pusat (merah) ke simpang (biru).

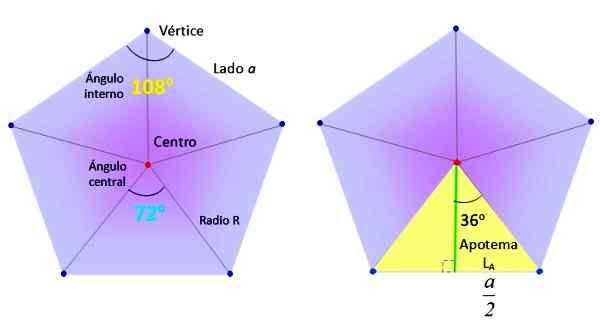Unsur -unsur yang diperlukan untuk mencari kawasan pentagon biasa. Sumber: f. Zapata.

Sebaliknya, segitiga, seperti kuning yang luar biasa di sebelah kanan di angka atas, dibahagikan kepada dua segi empat tepat yang sama, terima kasih kepada segmen hijau, yang dipanggil Apothem.

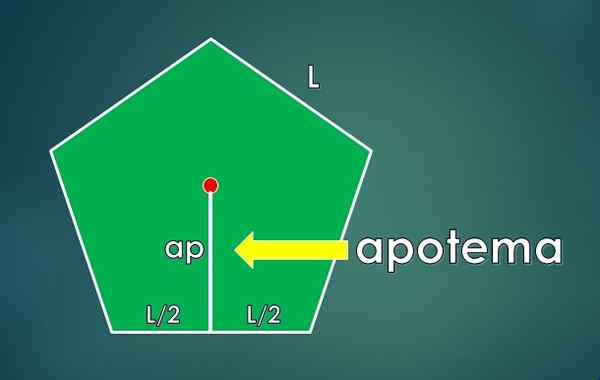
Apotheme ditakrifkan sebagai segmen tegak lurus yang menghubungkan ke pusat poligon dengan pusat satu sisi. Panjangnya l_Ke.

Kawasan segitiga segi empat tepat asas a/2 dan ketinggian l_Ke adalah:

[(A/2) x l_Ke]

Pentagon mempunyai 10 segitiga seperti ini, oleh itu kawasannya:

Boleh melayani anda: fungsi vektor

A = 10 (a/2) x l_Ke

Tetapi perimeter P Pentagon tepat p =10a, Oleh itu, kawasan itu diberikan oleh separuh produk perimeter dan panjang apothem:

A = p x l_Ke /2

Kawasan pentagon biasa mengetahui sisi a

Menyatakan panjang apothem l_Ke Bergantung pada sisi A, mengetahui bahawa sudut yang ditunjukkan adalah separuh sudut pusat, iaitu 36º, bersamaan dengan:

36º = π/5

Dengan trigonometri asas, dengan tangen sudut akut 36º:

Tan (π/5) = (a/2) ÷ l_Ke

Oleh itu:

L_Ke=  (A/2) ÷ tan (π/5)

Menggantikan di kawasan itu ditolak di bahagian sebelumnya, dan mengetahui bahawa p = 5a:

A = p x l_Ke /2

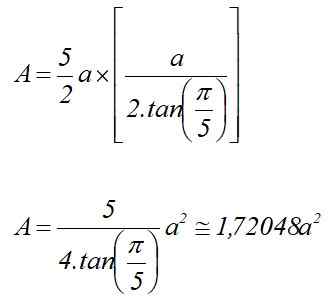
Kawasan pentagon biasa mengetahui radionya

Dia radio poligon biasa adalah segmen yang pergi dari pusat ke salah satu simpangnya. Ia bertepatan dengan jejari lilitan yang dilampirkan, seperti yang ditunjukkan dalam angka berikut:

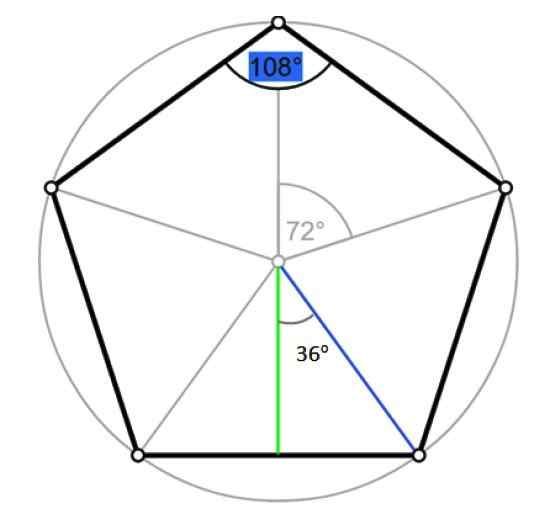Sudut dan Apothem Pentagon. Sumber: Wikimedia Commons/F. Zapata.

Biarkan R menjadi ukuran radio tersebut, yang bertepatan dengan hipotenus segitiga yang betul digambarkan dalam angka sebelumnya, dengan warna biru. Oleh trigonometri:

cos 36º = cos (π/5) = l_Ke ÷ r

Dan

dosa 36º = sin (π/5) = (a/2) ÷ r

Oleh itu:

A = p x l_Ke /2 = 5R. dosa (π/5) x r. cos (π/5) = 5R² [sin (π/5) x cos (π/5)]]

Menggunakan formula sudut berganda:

dosa (2θ) = 2 sen θ . cos θ

Kita mesti:

[sin (π/5) x cos (π/5)] = (1/2) Sin 72º

Oleh itu, dengan penggantian nilai ini, kami memperoleh formula berikut untuk kawasan Pentagon biasa:

A = (5/2) r².Sen 72º

Cara mengira kawasan pentagon yang tidak teratur?

Seperti yang telah kita katakan sebelum ini, untuk poligon yang tidak teratur tidak ada formula tunggal, tetapi terdapat dua kaedah yang biasanya berfungsi dengan baik, yang pertama dipanggil triangulasi dan yang kedua adalah kaedah penentu Gauss.

Boleh melayani anda: Teorem kewujudan dan keunikan: demonstrasi, contoh dan latihan

Triangulasi

Ia terdiri daripada membahagikan angka ke dalam segitiga, yang kawasannya lebih mudah dikira, atau juga boleh diuji dengan angka lain yang kawasannya diketahui, seperti dataran, segi empat tepat dan trapezida.

Penentu Gauss

Satu lagi cara untuk mencari kawasan pentagon yang tidak teratur atau poligon yang tidak teratur yang lain meletakkan angka dalam sistem koordinat Cartesian, untuk mencari koordinat simpang.

Dikenali koordinat ini, kaedah penentu Gauss digunakan untuk mengira kawasan tersebut, yang diberikan oleh formula berikut:

Di mana A adalah kawasan poligon dan (x_n , dan_n ) adalah koordinat simpang. Poligon dari sisi N mempunyai 5 simpang, untuk pentagon ia akan menjadi n = 5:

Bar yang mengiringi formula adalah bar modul atau nilai mutlak.

Ini bermakna walaupun hasil operasi itu negatif, kita mesti menyatakannya dengan tanda positif, dan jika sudah positif, ia mesti ditinggalkan dengan tanda itu. Ini kerana kawasan selalu menjadi jumlah yang positif.

Prosedur ini dipanggil penentu Gauss oleh penciptanya, ahli matematik Jerman Carl f. Gauss (1777-1855). Operasi yang ditunjukkan bersamaan dengan penentu matriks 2 × 2, contohnya penentu pertama ialah:

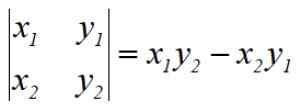
Untuk mencari kawasan pentagon kita mesti menyelesaikan 5 penentu, tambahkan hasilnya secara algebra, bahagikannya dengan 2 dan akhirnya menyatakan kawasan itu selalu dengan tanda positif.

Latihan yang diselesaikan

Latihan 1

Cari kawasan Pentagon biasa yang apotemnya bernilai 4 cm dan sampingannya mengukur 5.9 cm.

Penyelesaian

Oleh kerana ia adalah pentagon biasa, dan kami mempunyai ukuran sisi dan apothem, kami menggunakan formula yang ditolak sebelumnya:

Boleh melayani anda: Segitiga Scaleno

A = p x l_Ke /2

Perimeter p sama dengan 5a = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Latihan 2

Cari kawasan pentagon yang tidak teratur yang ditunjukkan. Dimensi berikut diketahui:

Dc ≈ of

Ae = ab = 5

BC = 12

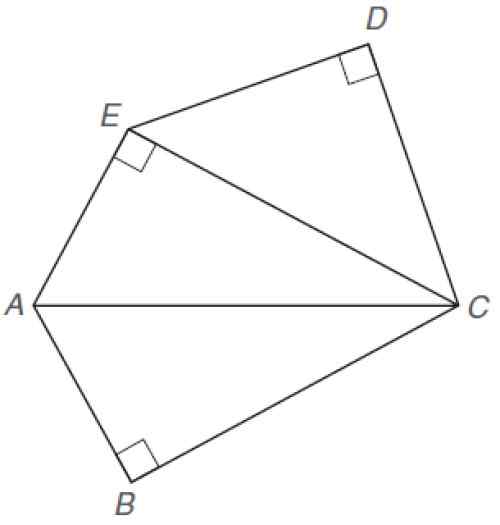Pentagon yang tidak teratur. Sumber: Alexander, D. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.

Penyelesaian

Kawasan Pentagon adalah jumlah kawasan segitiga, yang merupakan segi empat tepat. Kenyataan itu mengatakan bahawa dc ≈, oleh itu apabila menggunakan teorem Pythagoras ke segitiga EDC, ia mempunyai:

Ec² = 2 ed². Kemudian EC = √2.Ed.

Segitiga AEC dan ABC mempunyai hipotenus yang sama, iaitu segmen AC, oleh itu:

Ea² + Ec² = Ab² + BC²

Seperti yang diukur oleh EA dan AB yang sama, ia diperolehi:

EC = BC = √2.Ed

Oleh kerana BC = 12, kemudian ED = 12 / √2 = 8.485.

Dengan nilai -nilai ini kita akan mengira kawasan setiap segitiga dan menambahnya pada akhir.

Kawasan Segitiga EDC 

Ed x dc /2 = 8.485² / 2 = 36

Kawasan Segitiga AEC 

Ea x ec / 2 = ea x √2.Ed / 2 = 5 x √2. 8.485/2 = 30

Kawasan Segitiga ABC 

Ab x bc / 2

Kemudian kawasan yang dicari adalah:

5 x 12/2 = 30

Ia sama dengan segitiga AEC, kerana kedua -duanya mempunyai langkah yang sama.

Kawasan pentagon yang tidak teratur

Akhirnya kawasan yang diminta adalah jumlah kawasan tiga segitiga:

A = 36 + 30 + 30 unit = 96 unit.

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Rujukan terbuka matematik. Kawasan Poligon. Pulih dari: Mathpenref.com.
3. Formula Universe. Kawasan pentagon yang tidak teratur. Pulih dari: universoformulas.com.
4. Formula Universe. Kawasan pentagon biasa. Pulih dari: universoformulas.com.
5. Wikipedia. Pentagon. Pulih dari: Adakah.Wikipedia.com.