Formula Peraturan Simpson, Demonstrasi, Contoh, Latihan

The Peraturan Simpson Ia adalah kaedah untuk mengira, kira -kira, integral yang ditakrifkan. Ia berdasarkan membahagikan selang integrasi ke dalam sepasang sub-intervalos yang sama.

Nilai melampau dua sub-interval berturut-turut menentukan tiga mata, yang menyesuaikan parabola, yang persamaannya adalah polinomial darjah kedua. 

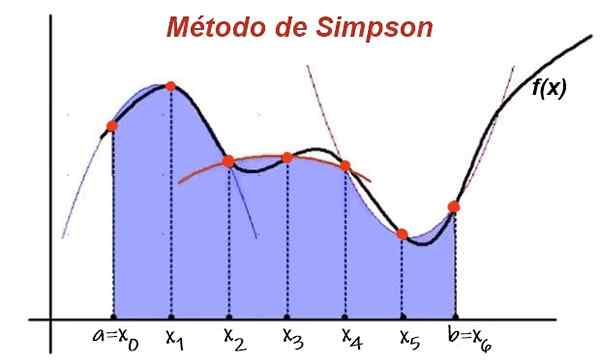
Rajah 1. Dalam kaedah Simpson, selang integrasi dibahagikan kepada sepasang selang lebar yang sama. Fungsi ini dianggarkan oleh perumpamaan dalam setiap 2 sub-intervalos dan pendekatan integral oleh jumlah kawasan di bawah perumpamaan. Sumber: UPV.adalah.

Kemudian kawasan di bawah lengkung fungsi dalam dua selang berturut -turut dianggarkan oleh kawasan polinomial interpolasi. Menambah sumbangan ke kawasan di bawah perumpamaan semua sub-interval berturut-turut, terdapat nilai anggaran yang penting.

Sebaliknya, kerana integral perumpamaan dapat dikira secara algebra secara tepat, maka adalah mungkin untuk mencari formula analisis untuk nilai anggaran integral yang ditetapkan. Dikenali sebagai Formula Simpson.

Kesalahan hasil anggaran yang diperolehi dengan demikian berkurangan setakat mana bilangan subdivisi n adalah lebih besar (menjadi tork) nombor.

Di bawah ekspresi akan diberikan yang membolehkan menganggarkan tahap atas kesilapan pendekatan kepada integral i, apabila pemisahan subintervals biasa dari jumlah selang [a, b] telah dibuat [b].

[TOC]

Formula

Selang integrasi [a, b] dibahagikan kepada subintervals n dengan n menjadi tork. Lebar setiap subdivisi akan:

H = (b - a)/n

Dengan cara ini, pada selang [a, b] partition dibuat:

X0, x1, x2, ..., xn-1, xn

Menjadi x0 = a, x1 = x0 + h, x2 = x0 + 2h, ..., xn-1 = x0 + (n-1) h, xn = x0 + nh = b.

Ia dapat melayani anda: perbezaan antara bulatan dan lilitan (dengan contoh)

Formula yang membolehkan kira -kira mengira fungsi integral dan berterusan yang ditetapkan, dan lebih baik lembut, dalam selang [a, b] adalah:

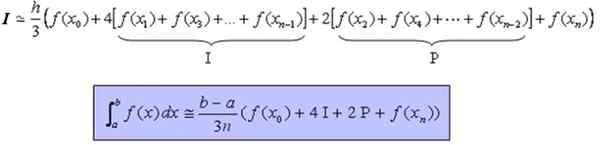
Demonstrasi

Untuk mendapatkan formula Simpson, dalam setiap subinterval [xi, xi+2] fungsi f (x) pendekatan dengan tahap kedua p (x) polinomial (perumpamaan) yang melewati tiga mata: [xi, f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f ( (F (F (F (F (F (F (F (F (F (F (F (F XI)]; [Xi+1, f (xi+1)] dan [xi+2, f (xi+2)]].

Kemudian polinomial integral p (x) dikira dalam [xi, xi+2] yang menghampiri integral fungsi f (x) dalam selang waktu itu.

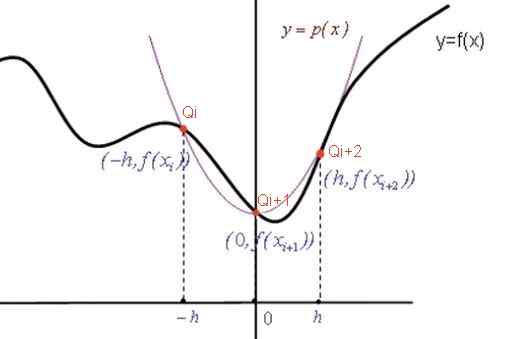Rajah 2. Graf untuk menunjukkan formula Simpson. Sumber: f. Zapata.

Koefisien polinomial interpolasi

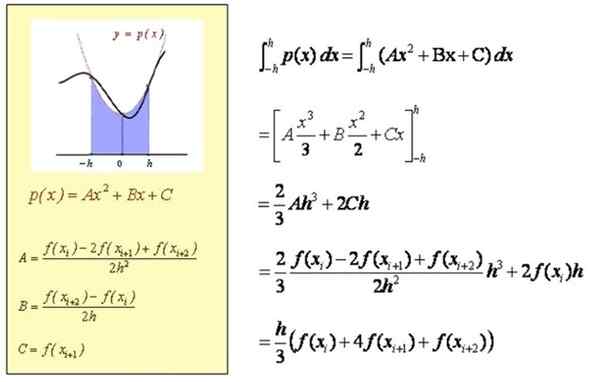
Persamaan parabola p (x) mempunyai bentuk umum: p (x) = a x² + B x + c. Oleh kerana perumpamaan itu melalui titik -titik yang ditunjukkan dalam warna merah (lihat angka), maka pekali a, b, c ditentukan dari sistem persamaan berikut:

A (-h)² - B h + c = f (xi)

C = f (xi+1)

A (h)² + B h + c = f (xi + 2)

Dapat diperhatikan bahawa pekali c ditentukan. Untuk menentukan pekali, kami menambah persamaan pertama dan ketiga yang diperoleh:

2 a h² + 2 c = f (xi) + f (xi + 2).

Kemudian nilai c diganti dan jelas:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 jam²)

Untuk menentukan pekali B, persamaan ketiga yang pertama dikurangkan dan B membersihkan dirinya:

B = [f (xi+2) - f (xi)] = 2 h.

Ringkasnya, polinomial tahap kedua P (x) yang melewati titik Qi, Qi+1 dan Qi+2 mempunyai pekali:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 jam²)

B = [f (xi+2) - f (xi)] = 2 h

C = f (xi+1)

Pengiraan integral anggaran dalam [xi, xi+2]

Pengiraan anggaran integral dalam [a, b]

Seperti yang telah dikatakan, pada selang integrasi keseluruhan [a, b] partition x0, x1, x2, ..., xn -1, xn dengan langkah h = xi+1 - xi = (b - (b -) / n, di mana n adalah pasangan.

Boleh melayani anda: ralat pensampelan: formula dan persamaan, pengiraan, contoh

Kemudian integral yang ditakrifkan dalam selang total [a, b] adalah jumlah integral dalam subintervals [xi, xi+2], yang didekati oleh integral polinomial interpolasi p (x):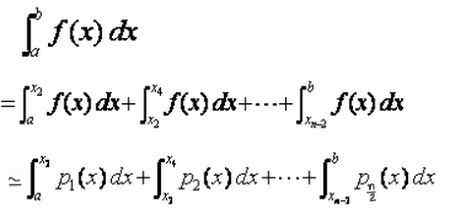

Di bahagian sebelumnya, formula untuk integral polinomial di subintervals dijumpai. Memohon hasil ini untuk setiap yang penting mempunyai: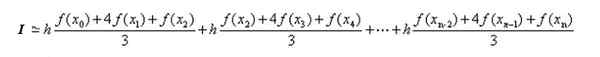

Yang boleh ditulis semula dengan cara yang lebih padat seperti berikut: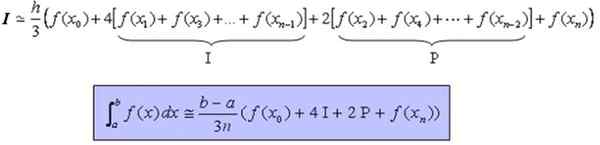

Kesalahan pendekatan

Sekiranya fungsi yang anda ingin berintegrasi ke dalam selang [a, b] telah diperolehi kepada urutan keempat, berterusan dalam selang itu, maka adalah mungkin untuk mencari formula yang membolehkan untuk menentukan tahap ralat maksimum dalam pendekatan dengan cara cara daripada Formula Simpson SN Untuk nilai integral: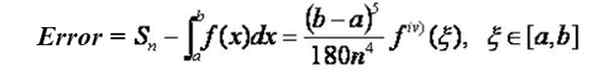

Perhatikan bahawa ralat berkurangan dengan kuasa keempat nombor subdivisi selang. Contohnya, jika anda pergi dari subdivisi n ke 2n, maka ralat berkurangan dengan faktor 1/16.

Tahap ralat atas yang diperolehi oleh pendekatan Simpson boleh diperolehi dari formula yang sama, menggantikan derivatif keempat dengan nilai mutlak maksimum derivatif keempat dalam selang [a, b].

Contoh yang diselesaikan

- Contoh 1

Pertimbangkan fungsi f (x) = 1 / (1 + x²). 

Cari integral fungsi f (x) yang ditetapkan dalam selang [-1, 1] menggunakan kaedah Simpson dengan dua subdivisi (n = 2).

Penyelesaian 

Diambil n = 2. Had integrasi adalah a = -1 dan b = -2, maka partition adalah seperti ini: 

X0 = -1; X1 = 0 dan x2 = +1.

Oleh itu, formula Simpson mengamalkan seperti berikut:

Dengan n = 2 → xo = -1, x1 = 0; x2 = 1, oleh itu:

- Contoh 2

Pertimbangkan fungsi f (x) = 1 / (1 + x²). 

Cari integral fungsi f (x) yang ditakrifkan dalam selang [-1, 1] oleh formula Simpson dengan empat subdivisi (n = 4).

Ia dapat melayani anda: anggaran mengikut selang waktu

Penyelesaian 

Diambil n = 4. Had integrasi adalah a = -1 dan b = -2, maka partition adalah seperti ini: 

X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 dan x4 = +1.

Formula Simpson ditubuhkan seperti berikut:

Integral ≃ [(b -A)/(3 n)] [f (x0) + 4 i + 2 p + f (xn)]

Untuk kes di mana ia digunakan, ia adalah seperti berikut:

Integral ≃ (1- (1))/(3 ⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)

Integral ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2 ⋅1 + ½] = (⅙) [47/5] = 47/30 = 1.5666

- Contoh 3

Tentukan integral yang jelas dari contoh -contoh sebelumnya dan membuat perbandingan hasil yang tepat dengan yang diperolehi oleh formula Simpson dalam Contoh 1a dan 1b.

Penyelesaian 

Integral tidak terbatas fungsi f (x) = 1 / (1 + x²) adalah fungsi Arctan (x).

Semasa menilai had integrasi:

Integral = arctan (1) - arctan (-1) = π/4 - (-π/4) = π/2 = 1,5708

Jika kita membandingkan hasil penyelesaian yang tepat dengan yang diperolehi oleh kaedah Simpson dengan n = 2 dan n = 4 kita ada:

Untuk n = 2 perbezaan antara penyelesaian yang tepat dan anggaran ialah π/2 -5/3 = -0959, iaitu perbezaan peratusan sebanyak -0.06%.

Dan untuk pendekatan Simpson dengan n = 4, perbezaan antara penyelesaian yang tepat dan anggaran ialah π/2 - 47/30 = 0.0041, iaitu perbezaan peratusan sebanyak 0.003%.

Latihan yang dicadangkan

Kaedah Simpson sesuai untuk digunakan dalam bahasa pengaturcaraan dan aplikasi komputer yang bertujuan untuk pengiraan matematik. Ia dicadangkan kepada pembaca yang, berdasarkan formula yang diberikan dalam artikel ini, tulis kodnya sendiri dalam program kegemarannya.

Angka berikut menunjukkan latihan di mana formula Simpson telah dilaksanakan di Smath Studio, Perisian percuma tersedia untuk sistem operasi Tingkap dan Android.

Rajah 3. Contoh integrasi berangka melalui peraturan Simpson menggunakan perisian. Sumber: f. Zapata.

Rujukan

1. Casteleiro, J. M. 2002. Pengiraan Komprehensif (Edisi Illustrated). Madrid: Editorial ESIC.
2. UPV. Kaedah Simpson. Universiti Politeknik Valencia. Pulih dari: youtube.com
3. Purcell, e. 2007. Pengiraan Edisi Kesembilan. Prentice Hall.
4. Wikipedia. Peraturan Simpson. Pulih dari: Adakah.Wikipedia.com
5. Wikipedia. Interpolasi polinomial LaGrange. Pulih dari: Adakah.Wikipedia.com