Sifat simetri pusat, contoh dan latihan

Dua mata a dan 'mempunyai simetri pusat Mengenai satu titik atau ketika segmen AA 'melaluinya dan juga titik tengah aa'. Ke titik atau dipanggil Pusat Simetri.

Simetri pusat segitiga ABC berkenaan dengan satu titik atau, adalah satu lagi segitiga a'b'c 'yang mempunyai ciri -ciri berikut:

-Segmen homolog adalah panjang yang sama 

-Sudut yang sepadan mereka mempunyai ukuran yang sama.

Rajah 1. Segitiga ABC dan simetri A'b'c '. Sumber: f. Zapata.

Dalam Rajah 1 segitiga ABC (merah) dan simetri pusat A'B'C '(hijau), berkenaan dengan pusat simetri atau. 

Dalam angka yang sama, pemerhati yang penuh perhatian akan menyedari bahawa hasil yang sama diperoleh dengan menggunakan putaran segitiga asal, selagi 180º dan fokus pada atau.

Oleh itu, simetri pusat bersamaan dengan giliran 180º berkenaan dengan pusat simetri.

[TOC]

Sifat simetri pusat

Simetri pusat mempunyai sifat berikut:

-Pusat simetri adalah titik tengah segmen yang bergabung dengan simetri.

-Titik simetri yang lain yang terletak di pusat simetri, bertepatan dengan pusat simetri.

-Simetri pusat segitiga adalah segitiga kongruen (sama) dengan yang asal.

-Imej oleh simetri pusat lilitan adalah satu lagi lilitan radius yang sama.

-Bulatan mempunyai simetri pusat berkenaan dengan pusatnya sendiri.

Rajah 2. Reka bentuk dengan simetri pusat. Sumber: Pixabay.

-Ellipse mempunyai simetri pusat berkenaan dengan pusatnya.

-Segmen mempunyai simetri pusat berkenaan dengan titik tengahnya.

-Segitiga sama rata tidak mempunyai simetri pusat berkenaan dengan pusatnya, kerana simetri, walaupun kongruen kepada yang pertama, memberikan segitiga sama rata.

Ia boleh melayani anda: tempoh fungsi y = 3sen (4x)

-Dataran mempunyai simetri pusat berkenaan dengan pusat mereka.

-Pentagon tidak mempunyai simetri pusat berkenaan dengan pusatnya.

-Poligon biasa mempunyai simetri pusat apabila mereka mempunyai sebilangan tork.

Contoh

Kriteria simetri mempunyai banyak aplikasi dalam sains dan kejuruteraan. Simetri pusat hadir dalam alam semula jadi, contohnya kristal ais dan labah -labah mempunyai simetri semacam ini.

Di samping itu, banyak masalah mudah diselesaikan apabila kewujudan simetri pusat dan jenis simetri lain digunakan. Oleh itu mudah untuk mengenal pasti dengan cepat apabila ia berlaku.

Rajah 3. Kristal ais mempunyai simetri pusat. Sumber: Pixabay.

Contoh 1

Memandangkan titik P koordinat (a, b), anda perlu mencari koordinat P 'simetri mengenai asal atau koordinat (0, 0).

Perkara pertama ialah membina p 'p', yang mana garis ditarik yang melalui asal atau dan melalui titik p. Persamaan garis ini ialah y = (b/a) x.

Sekarang mari kita panggil (a ', b') koordinat titik simetri p '. Titik p. Di samping itu, jarak OP mestilah sama dengan OP ', yang secara analitik menulis seperti ini:

√ (a² + b²) = √ (a '² + B '² )

Berikut adalah untuk menggantikan b '= [(b/a).A '] dalam ungkapan sebelumnya dan persegi di kedua -dua belah persamaan untuk menghapuskan akar kuadrat: (a² + b²) = [a '² + (b²/ke²).ke '²]

Dengan mengekstrak faktor biasa dan memudahkan, ia dicapai untuk '² = a². Persamaan ini mempunyai dua penyelesaian sebenar: a '= +a atau a' = -a. 

Untuk mendapatkan b ', kami menggunakan lagi b' = (b/a) a '. Sekiranya penyelesaian positif A diganti, ia dicapai bahawa b '= b. Dan apabila penyelesaian negatif diganti, maka b '= -b. 

Boleh melayani anda: Apakah 7 elemen lilitan?

Penyelesaian positif memberikan p 'titik yang sama p, jadi ia diketepikan. Penyelesaian negatif pasti menawarkan koordinat titik simetri:

P ': (-a, -b)

Contoh 2

Dikehendaki menunjukkan bahawa segmen ab dan pusat simetri A'b 'mempunyai panjang yang sama.

Bermula dengan koordinat titik A, yang (kapak, ay) dan titik -titik b: (bx, by), panjang ab diberikan oleh:

D (ab) = √ ((bx - kapak)² + (Oleh - ay)² )

Dengan analogi, segmen simetri A'b 'akan mempunyai panjang yang diberikan oleh:

d (a'b ') = √ ((bx' - ax ')² + (Oleh ' - ay')² )

Koordinat titik simetri A 'adalah kapak' = -ax dan ay '= -ay. Begitu juga dengan b 'adalah bx' = -bx dan oleh '= -by. Jika koordinat ini digantikan dalam persamaan jarak d (a'b ') anda mempunyai:

D (a'b ') = √ ((-bx + ax)² + (-By + ay)²) yang bersamaan dengan:

 √ ((bx - kapak)² + (Oleh - ay)²) = D (ab)

Ditunjukkan bahawa kedua -dua segmen mempunyai panjang yang sama.

Latihan yang diselesaikan

- Latihan 1

Menunjukkan dengan cara analitik bahawa simetri pusat atau bulatan radius r dan pusat atau, adalah lilitan asal yang sama.

Penyelesaian

Persamaan radius r dan bulatan tengah (0.0) adalah:

x² + dan² = R² (Persamaan lilitan c)

Jika pada setiap titik p lilitan dan koordinat (x, y) koordinat simetri P ') dijumpai, persamaan lilitan simetri adalah:

x '² + dan '² = R² (Persamaan Lingkaran Simetri C ')

Sekarang kita merujuk kepada hasil Contoh 1, yang menyimpulkan bahawa koordinat titik p ', simetri kepada p dan koordinat (a, b), adalah (-a, -b). 

Tetapi dalam latihan ini, titik p mempunyai koordinat (x, y), jadi smmetrical p 'akan mempunyai koordinat x' = -x e y '= -y. Menggantikan ini dalam persamaan lilitan simetri ialah:

Boleh melayani anda: rhomboid: ciri -ciri, cara mengeluarkan perimeter dan kawasan

(-X)² + (-and)² = R²

Yang bersamaan dengan: x²+ dan² = R², menyimpulkan bahawa simetri pusat bulatan berkenaan dengan pusatnya adalah lilitan itu sendiri.

- Latihan 2

Menunjukkan dengan cara geometri bahawa simetri pusat mengekalkan sudut.

Penyelesaian

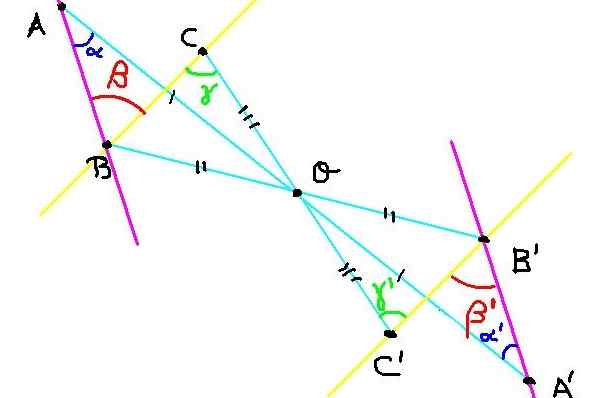Rajah 4. Pembinaan Mata Simetri untuk Latihan 2. Sumber: f. Zapata.

Terdapat tiga mata A, B dan C di pesawat. Simetri A ', b' dan c 'dibina berkenaan dengan pusat simetri atau, seperti yang ditunjukkan dalam Rajah 4. 

Sekarang kita mesti menunjukkan bahawa sudut ∡abc = β mempunyai ukuran yang sama dengan sudut ∡a'b'c '= β' '.

Sebagai c dan c 'simetri, maka oc = oc'. Begitu juga ob = ob 'y oa = oa'. Sebaliknya, sudut ∡boc = ∡b'oc 'kerana menentang puncak.

Kemudian segitiga boc dan b'oc 'adalah kongruen kerana mempunyai sudut yang sama antara dua sisi sama.

Kerana boc bersesuaian dengan b'oc 'maka sudut  γ dan γ ' Mereka sama. Tetapi sudut -sudut ini, selain memenuhi γ = γ ' Mereka adalah pengganti dalaman antara garis BC dan B'c 'yang menunjukkan bahawa garis BC selari dengan b'c'.

Begitu juga Baa adalah kongruen dengan b'oa 'dari apa yang diikuti α = α ' . Tetapi  α dan α ' Mereka adalah sudut alternatif dalaman antara garis Ba dan B'a ', yang mana disimpulkan bahawa garis Ba selari dengan B'a'.

Seperti sudut ∡ABC = β mempunyai sisi selari dengan sudut ∡a'b'c '= β' dan juga kedua -duanya akut ia menyimpulkan bahawa:

∡abc = ∡a'b'c '= β = β' '

Menunjukkan dengan cara ini bahawa simetri pusat mengekalkan ukuran sudut.

Rujukan

1. Baldor, j. Ke. 1973.Geometri rata dan ruang. Kebudayaan Amerika Tengah. 
2. Undang -undang dan formula matematik. Sistem pengukuran sudut. Diperolehi dari: Ingemecanica.com.
3. Wentworth, g. Geometri Planet. Pulih dari: gutenberg.org.
4. Wikipedia. Simetri pusat. Pulih dari: Adakah.Wikipedia.com
5. Wikipedia. Penghantar. Pulih dari: Adakah.Wikipedia.com
6. Zapata f. Sudut konjugasi dalaman dan luaran. Diperolehi dari: Lifer.com