Sistem oktal

Apa itu sistem oktal?

Dia Sistem oktal Ia adalah sistem penomboran asas lapan (8); Iaitu, ia terdiri daripada lapan digit, iaitu: 0, 1, 2, 3, 4, 5, 6 dan 7. Oleh itu, setiap digit nombor oktal boleh mempunyai nilai dari 0 hingga 7. Nombor oktal terbentuk dari nombor binari.

Ini kerana pangkalannya adalah kuasa tepat dua (2). Iaitu, angka -angka yang dimiliki oleh sistem oktal dibentuk apabila mereka dikelompokkan menjadi tiga digit berturut -turut, diperintahkan dari kanan ke kiri, sehingga memperoleh nilai perpuluhan mereka.

Sejarah Sistem Octal

Sistem oktal mempunyai asalnya pada zaman purba, ketika orang menggunakan tangan mereka untuk mengira lapan oleh lapan haiwan.

Sebagai contoh, untuk mengira bilangan lembu di stabil, tangan kanan mula mempunyai ibu jari dengan jari kecil; Kemudian untuk mengira haiwan kedua, ibu jari bersatu dengan jari telunjuk, dan sebagainya dengan jari -jari yang tersisa di setiap tangan, sehingga selesai 8.

Terdapat kemungkinan bahawa sistem penomboran oktal sebelum perpuluhan dapat mengira ruang interdigital; iaitu, beritahu semua jari kecuali ibu jari.

Seterusnya, sistem penomboran oktal ditubuhkan, yang berasal dari sistem binari, kerana ia memerlukan banyak digit untuk mewakili hanya satu nombor; Sejak itu, sistem oktal dan heksagon dicipta, yang tidak memerlukan begitu banyak digit dan yang boleh ditukar dengan mudah ke sistem binari.

Sistem penomboran oktal

Sistem oktal terdiri daripada lapan digit antara 0 hingga 7. Ini mempunyai nilai yang sama seperti dalam kes sistem perpuluhan, tetapi perubahan nilai relatif mereka bergantung pada kedudukan yang diduduki ini. Nilai setiap kedudukan diberikan oleh kuasa asas 8.

Ia boleh melayani anda: Peraturan T: Ciri -ciri, supaya ia, contohnya

Kedudukan digit dalam nombor oktal mempunyai peso berikut:

8⁴, 8³, 8², 8¹, 8⁰, Titik oktal, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Digit oktal utama ialah 7; Dengan cara ini, apabila dikira dalam sistem ini kedudukan digit dari 0 hingga 7 semakin meningkat. Apabila ia mencapai 7 ia dikitar semula pada 0 untuk kiraan seterusnya; Ini meningkatkan kedudukan digit berikut. Sebagai contoh, untuk mengira urutan, dalam sistem oktal ia akan menjadi:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Terdapat teorem asas yang digunakan untuk sistem oktal, dan dinyatakan seperti berikut:

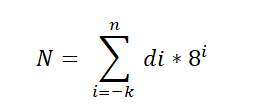
Dalam ungkapan ini di mewakili digit yang didarabkan oleh kuasa 8 kuasa, yang menunjukkan nilai posisi setiap digit, dengan cara yang sama di mana ia diperintahkan dalam sistem perpuluhan.

Contohnya, anda mempunyai nombor 543.2. Untuk membawanya ke sistem oktal, ia terurai seperti berikut:

N = Σ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0.125)

N = 320 +32 + 2 + 0.25 = 354 + 0.25_d

Dengan cara itu anda mempunyai 543.2_q = 354.25_d. Subskrip yang menunjukkan bahawa ia adalah nombor oktal yang juga boleh diwakili oleh nombor 8; dan subskrip d merujuk kepada nombor perpuluhan, yang juga boleh diwakili dengan nombor 10.

Penukaran sistem oktal ke perpuluhan

Untuk menukar nombor sistem oktal dengan setara dengan sistem perpuluhan, setiap digit oktal harus didarab dengan nilai kedudukannya, bermula dari kanan.

Contoh 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Dapat melayani anda: kesaksamaan matematik

Contoh 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0.125)

26.9₈ = 16 + 6 + 1.125

26.9₈= 23,125₁₀

Penukaran sistem perpuluhan ke oktal

Integer perpuluhan boleh ditukar menjadi nombor oktal menggunakan kaedah pembahagian berulang, di mana integer perpuluhan dibahagikan dengan 8 sehingga kuota adalah sama dengan 0, dan pembaziran setiap bahagian akan mewakili nombor oktal.

Sisa itu diperintahkan dari yang terakhir ke yang pertama; iaitu, sisa pertama akan menjadi digit paling ketara bagi nombor oktal. Dengan cara ini, digit yang paling penting akan menjadi sisa terakhir.

Contoh

Oktal nombor perpuluhan 266₁₀

- Nombor perpuluhan 266 dibahagikan dengan 8 = 266/8 = 33 + 2 residu.

- Maka 33 dibahagikan dengan 8 = 33/8 = 4 + 1 sisa.

- 4 dibahagikan dengan 8 = 4/8 = 0 + 4 residu.

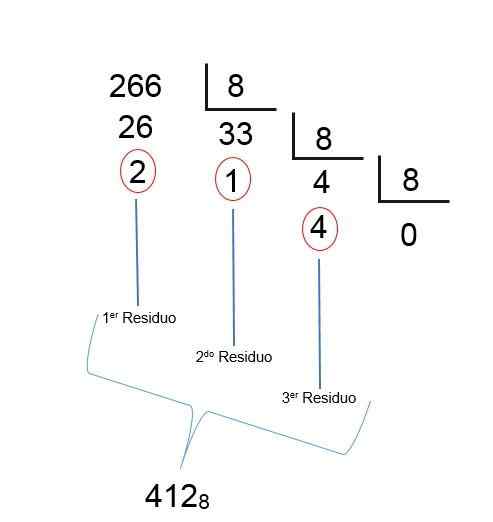
Seperti bahagian terakhir yang kurang daripada 1 diperolehi, ini bermakna hasilnya telah dijumpai; Hanya jenazah yang perlu dipesan secara terbalik, supaya bilangan octal perpuluhan 266 adalah 412, seperti yang dapat dilihat dalam imej berikut:

Penukaran sistem oktal binari

Penukaran oktal ke sistem binari dijalankan ketika menukar angka oktal ke digit binari setara, dibentuk oleh tiga digit. Terdapat jadual yang menunjukkan bagaimana lapan digit yang mungkin menjadi:

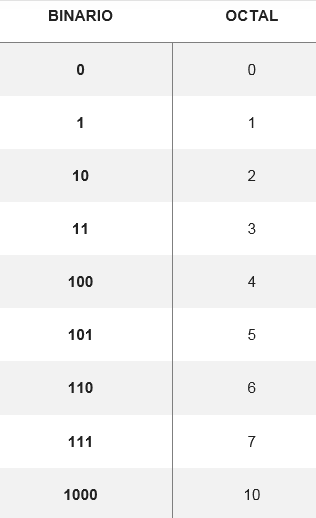
Dari penukaran ini, anda boleh menukar bilangan sistem oktal ke binari, seperti untuk menukar nombor 572₈ Kesamaan anda dicari di atas meja. Oleh itu, anda mesti:

5₈ = 101

7₈= 111

2₈ = 10

Oleh itu, 572₈ Bersamaan dengan sistem binari hingga 10111110.

Sistem binari ke penukaran oktal

Proses penukaran nombor integral kepada bilangan bulat oktal adalah operasi terbalik ke proses sebelumnya.

Dapat melayani anda: apakah unsur -unsur sudut?

Iaitu, bit nombor binari dikelompokkan kepada dua kumpulan tiga bit, bermula dari kanan ke kiri. Kemudian, penukaran binari ke oktal dibuat dengan jadual sebelumnya.

Dalam beberapa kes, nombor binari tidak akan mempunyai kumpulan 3 bit; Untuk menyelesaikannya, satu atau dua sifar ditambah ke kiri kumpulan pertama.

Sebagai contoh, untuk menukar nombor binari 11010110 ke oktal yang berikut dilakukan:

- Kumpulan 3 bit dibentuk bermula di sebelah kanan (bit terakhir):

11010110

- Oleh kerana kumpulan pertama tidak lengkap, sifar ditambah ke kiri:

011010110

- Penukaran dibuat dari jadual:

011 = 3

010 = 2

110 = 6

Dengan cara ini, nombor binari 011010110 bersamaan dengan 326₈.

Penukaran sistem oktal ke heksadesimal dan sebaliknya

Untuk menukar nombor oktal ke hexadecimal atau hexadecimal kepada sistem oktal, perlu bilangannya akan menjadi binari terlebih dahulu, dan kemudian ke sistem yang dikehendaki.

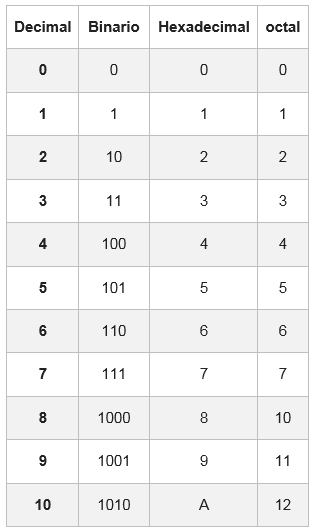
Untuk ini terdapat jadual di mana setiap digit heksadesimal diwakili dengan kesetaraannya dalam sistem binari, terdiri daripada empat digit.

Dalam beberapa kes, nombor binari tidak akan mempunyai kumpulan 4 bit; Untuk menyelesaikannya, satu atau dua sifar ditambah ke kiri kumpulan pertama

Contoh

Tukar nombor oktal 1646 ke dalam nombor heksadesimal:

- Octal ke nombor binari menjadi

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Oleh itu, 1646₈ = 1110100110.

- Untuk menukar dari binari ke heksadesimal, mereka mula -mula diperintahkan dalam sekumpulan 4 bit, bermula dari kanan ke kiri:

11 1010 0110

- Kumpulan pertama disiapkan dengan sifar, supaya ia boleh mempunyai 4 bit:

0011 1010 0110

- Penukaran sistem binari heksadesimal dibuat. Kesetaraan digantikan dengan jadual:

0011 = 3

1010 = a

0110 = 6

Dengan cara ini, nombor oktal 1646 bersamaan dengan 3A6 dalam sistem heksadesimal.