Revolusi pepejal, jenis, latihan yang diselesaikan

Dia Revolusi pepejal Ia adalah angka tiga dimensi yang dihasilkan oleh putaran permukaan rata di sekitar paksi paksi atau paksi revolusi. Rajah 1 menunjukkan animasi pepejal revolusi yang dihasilkan dengan cara ini.

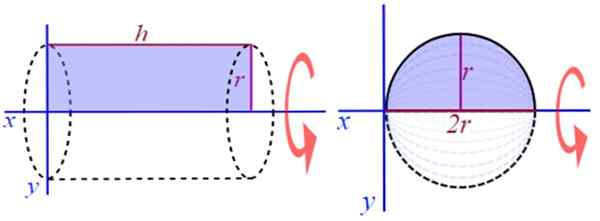
Satu lagi contoh yang sangat mudah untuk digambarkan adalah untuk menjana silinder bulat lurus, berputar segi empat tepat ketinggian atau panjang H dan Radio R, sekitar paksi x positif (Rajah 2). Untuk mencari kelantangannya terdapat formula yang terkenal:

V = kawasan asas x ketinggian

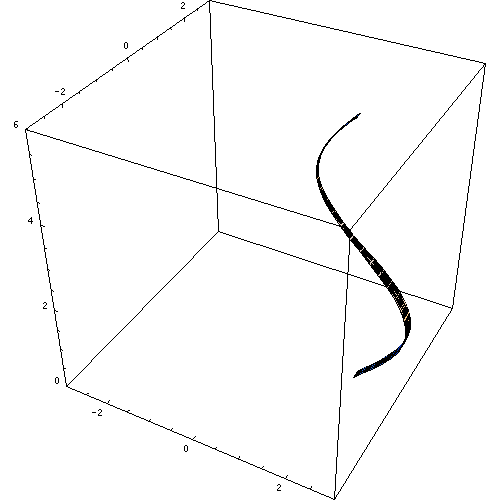Rajah 1. Angka yang dihasilkan oleh putaran lengkung sen x. Sumber: Wikimedia Commons. Macks/cc by-sa (https: // creativeCommons.Org/lesen/by-sa/2.5).

Pepejal revolusi lain adalah sfera, kerucut pekeliling lurus dan pelbagai angka, mengikut permukaan yang diletakkan dalam putaran dan tentu saja, paksi yang dipilih.

Rajah 2. Penjanaan silinder bulat lurus dan sfera. Sumber: Wikimedia Commons.

Sebagai contoh, berputar separuh bulatan sekitar garis selari dengan diameter pepejal revolusi berongga diperolehi.

Untuk silinder, kerucut, sfera, kedua -dua massifs dan lubang, ada formula untuk mencari kelantangan, yang bergantung pada jejari dan ketinggian. Tetapi apabila dihasilkan oleh permukaan lain, jumlahnya dikira oleh integral yang ditetapkan.

[TOC]

Jenis pepejal revolusi

Pepejal Revolusi boleh diklasifikasikan mengikut lengkung yang menghasilkannya:

Sfera

Cukup untuk memutar separuh bulatan di sekitar paksi yang akan menjadi diameter sfera radio r. Jumlahnya ialah:

V_sfera = (4/3) πr³

Pussy

Untuk mendapatkan kerucut H dan Radio R, permukaan yang mesti. Jumlahnya ialah:

V_Pussy = (1/3) πhr²

Silinder

Putar segi empat tepat di sekitar paksi paksi yang melewati satu sisi, yang boleh menjadi sisi pendek atau sisi panjang, silinder bulat lurus radius r dan ketinggian H diperolehi, yang jumlahnya:

Boleh melayani anda: tali (geometri): panjang, teorem dan latihan

V_silinder = πr²H

Toroid

Lembu mempunyai bentuk donat. Ia diperolehi dengan memutar kawasan bulat di sekitar garis dalam satah yang tidak merentasi bulatan. Jumlahnya diberikan oleh:

V_Toroid = 2πa²R

Di mana A adalah jejari bahagian silang dan r ialah jejari toroid mengikut skema yang dibentangkan dalam gambar:

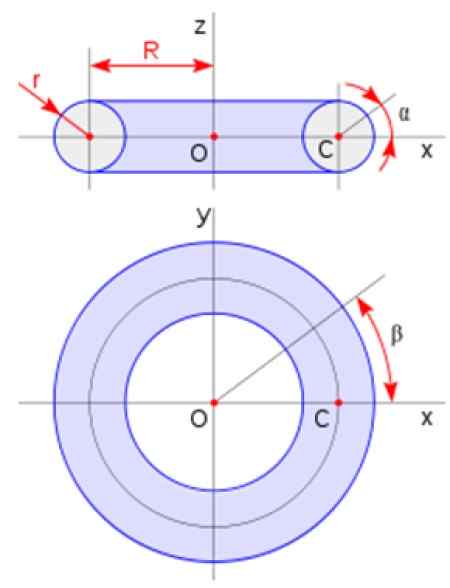Rajah 3. Dimensi toroid. Sumber: Wikimedia Commons.

Kaedah untuk mengira jumlah pepejal revolusi

Dalam pengiraan integral kedua -dua kaedah ini adalah kerap:

-Cakera dan pencuci

-Kerang

Kaedah cakera atau pencuci

Apabila memotong pepejal revolusi, bahagian silang boleh menjadi album, jika pepejal adalah pepejal atau ia boleh menjadi sejenis mesin basuh (album dengan lubang di tengah), jika ia adalah lubang pepejal.

Katakan kawasan rata diputar di sekitar paksi mendatar. Dari kawasan rata itu kita mengambil segi empat tepat lebar Δx kecil, yang diputar serentak di sekitar paksi paksi.

Ketinggian segi empat tepat antara lengkung paling luar r (x) dan r (x) yang paling dalaman. Mereka sesuai dengan jejari luaran dan radio dalaman masing -masing.

Apabila membuat putaran ini, mesin basuh volum ΔV dihasilkan, diberikan oleh:

ΔV = kelantangan penuh - jumlah lubang (jika ada)

Mengingati bahawa jumlah silinder bulat lurus adalah π. radio² x ketinggian, kita ada:

ΔV = π [r²(x) - r²(x)] Δx

Pepejal boleh dibahagikan kepada banyak bahagian kecil kelantangan ΔV. Sekiranya kita menambahkan semuanya, kita akan mempunyai jumlah penuh.

Untuk melakukan ini kita akan cenderung kepada 0 isipadu ΔV, yang juga menjadi sangat kecil, menjadi perbezaan dx.

Ia boleh melayani anda: Peristiwa yang tidak bersekutu: sifat dan contohnya

Oleh itu kita mempunyai integral:

V = ∫_ke^b π [r²(x) - r²(x)] dx

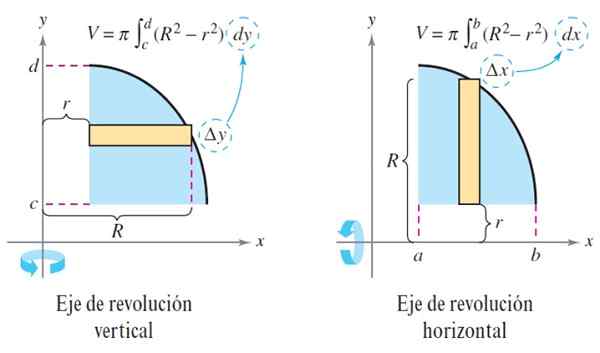Rajah 3. Kaedah pencuci. Sumber: Larson. R. Pengiraan.

Sekiranya pepejal adalah pepejal, maka fungsi r (x) = 0, kepingan pepejal yang dihasilkan adalah cakera dan jumlahnya tetap:

V = ∫_ke^b πr²(x) dx

Apabila paksi revolusi menegak, persamaan sebelumnya mengambil bentuk:

V = ∫_ke^b π [r² (Y) - r² (y)] dy dan v = ∫_ke^b πr²(Y) dy

Lapisan

Seperti yang ditunjukkan oleh nama, kaedah ini adalah untuk mengandaikan bahawa pepejal terdiri daripada lapisan tebal berbeza. Lapisan adalah tiub nipis yang berasal dari giliran segi empat tepat selari dengan paksi putaran.

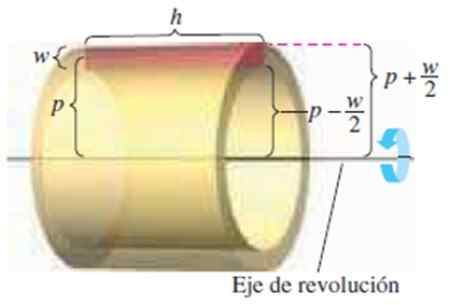Rajah 4. Lapisan ketinggian silinder 2, panjang h dan radius p. Sumber: Larson, r. Pengiraan.

Kami mempunyai dimensi berikut:

-Ketinggian segi empat tepat W

-Bujurnya h

-Jarak dari pusat segi empat tepat ke paksi putaran p

Mengetahui bahawa kelantangan lapisan Jilid Luaran - Jilid Interior:

π (p + w/2)²H - π (p - w/2)²h

Apabila membangunkan produk yang ketara dan memudahkan, ia diperolehi:

Kelantangan lapisan = 2π angani pp angani

Sekarang mari kita membuat ketinggian w dari segi empat tepat Δy, seperti yang dilihat dalam angka berikut:

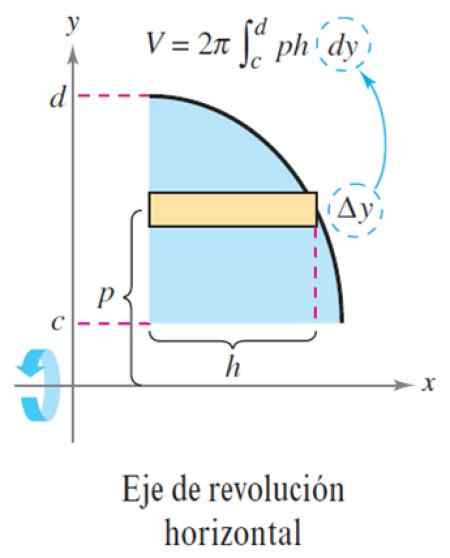Rajah 5. Kaedah lapisan paksi revolusi mendatar. Sumber: Larson, r. Pengiraan pemboleh ubah.

Dengan ini kelantangan ΔV ialah:

ΔV = 2π p x h x Δy

Dan membuat bilangan lapisan n Jadilah sangat besar, ΔY menjadi pembezaan dy, sehingga jumlah jumlahnya adalah integral:

V = ∫_c^d 2π p (y) h (y) dy

Prosedur yang diterangkan digunakan sama apabila paksi revolusi adalah menegak:

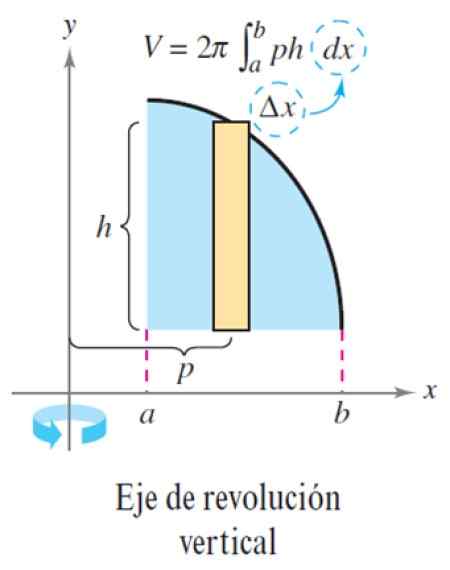Rajah 6. Kaedah lapisan untuk paksi revolusi menegak. Sumber: Larson, r. Pengiraan pemboleh ubah.

Latihan diselesaikan

Cari kelantangan yang dihasilkan oleh putaran kawasan rata antara lengkung:

y = x²;  y = 0; x = 2

Sekitar paksi dan.

Boleh melayani anda: homotecia negatif

Penyelesaian

-Perkara pertama yang perlu dilakukan ialah graf rantau yang akan menjana revolusi pepejal dan menunjukkan paksi giliran. Kami memilikinya dalam graf berikut:

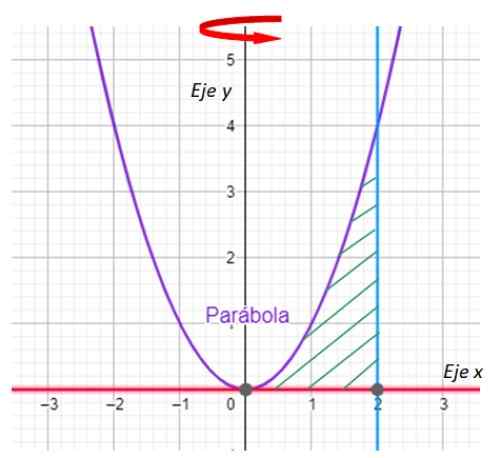Rajah 7. Graf lengkung untuk latihan diselesaikan. Sumber: f. Zapata dengan geogebra.

-Sekarang persimpangan antara lengkung y = x dicari² dan garis x = 2. Bagi bahagiannya garis y = 0 tidak lain daripada paksi x.

Sangat mudah untuk memberi amaran bahawa perumpamaan dan garis bersilang pada titik (2,4), yang disokong dengan menggantikan x = 2 pada y = x².

-Kemudian salah satu kaedah untuk mengira kelantangan dipilih, contohnya kaedah lapisan dengan paksi revolusi menegak:

V = ∫_ke^b 2π p (x) h (x) dx

Langkah 1: Lukis segi empat tepat

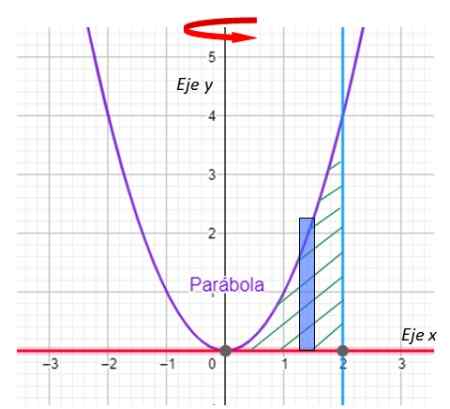Rajah 8. Segi empat tepat untuk contoh yang diselesaikan. Sumber: f. Zapata dengan geogebra.

Penting: Dalam kaedah lapisan, sisi panjang segi empat tepat selari dengan paksi putaran.

Langkah 2: Tentukan P (x)

Lapisan lapisan adalah x

Langkah 3: Tentukan H (x)

Ketinggian segi empat tepat ditentukan oleh perumpamaan x².

Langkah 4: Menetapkan dan selesaikan jumlah integral

Pemboleh ubah integrasi adalah x, yang berbeza antara 0 dan 2, dengan ini kita mempunyai had integrasi. Menggantikan ungkapan untuk p (x) dan h (x)

 Beberapa latihan dapat diselesaikan dengan kedua -dua kaedah. Bolehkah pembaca menyelesaikannya dengan kaedah pencuci?

Rujukan

1. Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.
2. Purcell, e. 2007. Pengiraan dengan geometri analisis. 9NA. Edisi. Pendidikan Pearson.
3. Wikipedia. Pepejal revolusi. Diperoleh dari: dalam.Wikipedia.org.
4. Wikipedia. Toroid. Pulih dari: Adakah.Wikipedia.org.
5. Wolfram Mathworld. Pepejal revolusi. Pulih dari: Mathworld.Wolfram.com.