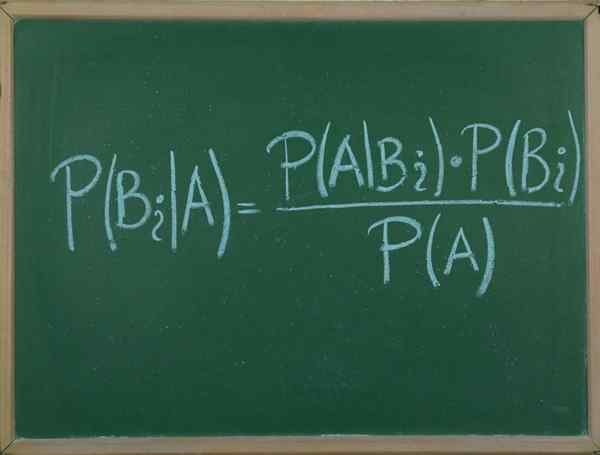Teorem Bayes
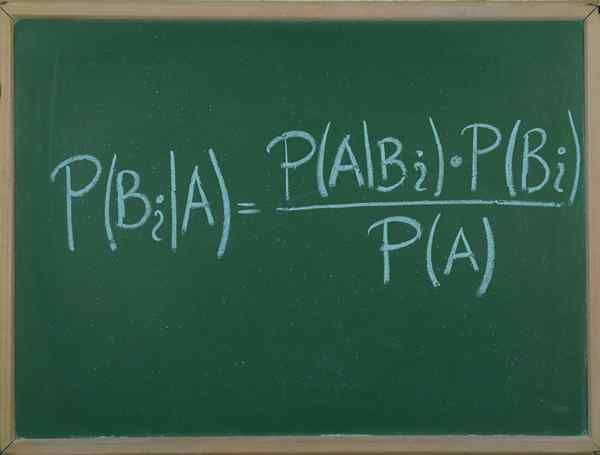
- 3329
- 402
- Dallas Bernhard
Kami menerangkan apa teorem Bayes, aplikasinya dan kami meletakkan latihan yang diselesaikan
Apa itu Teorem Bayes?
Dia Teorem Bayes Ini adalah prosedur yang membolehkan kita menyatakan kebarangkalian bersyarat peristiwa rawak dadu B, dari segi pengagihan kebarangkalian peristiwa B yang diberikan dan taburan kebarangkalian hanya untuk.
Teorem ini sangat berguna, kerana terima kasih kita dapat mengaitkan kebarangkalian bahawa peristiwa A berlaku mengetahui bahawa B sedang berlaku, dengan kebarangkalian bahawa sebaliknya berlaku, iaitu, ia terjadi diberikan kepada.
Teorem Bayes adalah cadangan perak oleh Reverend Thomas Bayes, ahli teologi Inggeris abad ke -18 yang juga seorang ahli matematik. Beliau adalah pengarang beberapa pekerjaan dalam teologi, tetapi pada masa ini dia terkenal dengan beberapa perjanjian matematik, di antaranya teorem Bayes telah disebut sebagai hasil utama.
Bayes menangani teorem ini dalam karya bertajuk "An Essay Menuju Penyelesaian Masalah Dalam Doktrin Peluang" (Satu esei untuk menyelesaikan masalah dalam doktrin kemungkinan), yang diterbitkan pada tahun 1763, dan di mana besar telah mengembangkan kajian dengan aplikasi dalam pelbagai bidang pengetahuan.
Penjelasan
Pertama, untuk pemampatan yang lebih besar dari teorem ini, beberapa tanggapan asas teori kebarangkalian diperlukan, terutama teorem pendaraban untuk kebarangkalian bersyarat, yang menetapkan bahawa
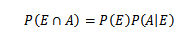
Untuk E dan ke peristiwa sewenang -wenang ruang sampel s.
Dan definisi partisi, yang memberitahu kita bahawa kita ada1 ,Ke2,..., kepadan peristiwa ruang sampel, ini akan membentuk partition s, jika aYo Mereka saling eksklusif dan kesatuan mereka adalah s.
Boleh melayani anda: Apakah nombornya? 8 kegunaan utamaMemiliki ini, sama ada acara lain. Oleh itu, kita dapat melihat b sebagai
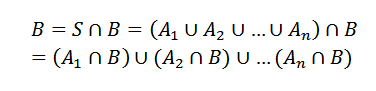
Di mana aYo Bersilang dengan B adalah peristiwa yang saling eksklusif.
Dan akibatnya,
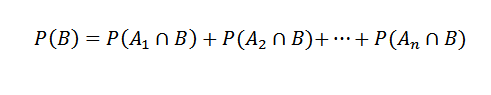
Kemudian, memohon teorem pendaraban
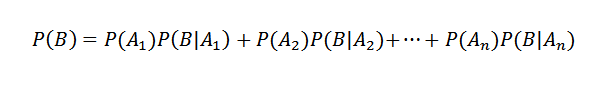
Sebaliknya, kebarangkalian bersyarat AI B ditakrifkan oleh
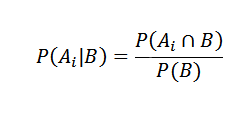
Menggantikan dengan betul kita ada untuk mana -mana i
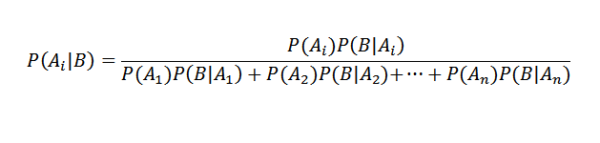
Aplikasi Teorem Bayes
Terima kasih kepada hasil ini, kumpulan penyelidikan dan pelbagai syarikat telah berjaya memperbaiki sistem yang berdasarkan pengetahuan.
Kajian penyakit
Sebagai contoh, dalam kajian penyakit, teorem Bayes dapat membantu membezakan kebarangkalian bahawa penyakit akan dijumpai dalam sekumpulan orang yang mempunyai ciri -ciri tertentu, mengambil data kadar penyakit global dan dominasi ciri -ciri tersebut dalam kedua -dua Orang yang sihat dan sakit.
Pembangunan perisian
Sebaliknya, di dunia teknologi tinggi, ia telah mempengaruhi syarikat besar yang telah dibangunkan, terima kasih kepada hasil ini, perisian "berdasarkan pengetahuan".
Sebagai contoh harian kita mempunyai pembantu pejabat microsoft. Teorem Bayes membantu perisian untuk menilai masalah yang dibentangkan oleh pengguna dan menentukan nasihat yang hendak diberikan dan dengan itu dapat menawarkan perkhidmatan yang lebih baik mengikut tabiat pengguna.
Harus diingat bahawa formula ini diabaikan sehingga kebelakangan ini, ini adalah kerana apabila hasil ini dibangunkan 200 tahun yang lalu, terdapat sedikit penggunaan praktikal untuk mereka. Walau bagaimanapun, pada masa kita, terima kasih kepada kemajuan teknologi yang hebat, saintis telah mencapai cara untuk meletakkan hasil ini menjadi amalan.
Latihan yang diselesaikan
Latihan 1
Syarikat telefon bimbit mempunyai dua mesin A dan B. 54% telefon bimbit dibuat oleh mesin A dan selebihnya oleh mesin b. Tidak semua telefon bimbit berada dalam keadaan baik.
Boleh melayani anda: pemfaktoranPerkadaran telefon bimbit yang cacat yang dibuat oleh A ialah 0.2 dan untuk B ialah 0.5. Apakah kebarangkalian bahawa telefon bimbit kilang tersebut rosak? Apakah kebarangkalian bahawa, mengetahui bahawa telefon bimbit rosak, berasal dari mesin ke?
Penyelesaian
Di sini, anda mempunyai eksperimen yang dilakukan dalam dua bahagian; Pada bahagian pertama peristiwa berlaku:
Ke: telefon bimbit yang dibuat oleh mesin a.
B: Telefon bimbit yang dibuat oleh mesin b.
Oleh kerana mesin A menghasilkan 54% telefon bimbit dan selebihnya dihasilkan oleh mesin B, mesin B harus menghasilkan 46% telefon bimbit. Kemungkinan peristiwa -peristiwa ini diberikan, iaitu:
P (a) = 0.54.
P (b) = 0.46.
Peristiwa bahagian kedua eksperimen adalah:
D: Telefon bimbit yang cacat.
E: Sel tidak aktif.
Seperti yang dinyatakan dalam kenyataan itu, kebarangkalian peristiwa ini bergantung kepada hasil yang diperolehi di bahagian pertama:
P (D | A) = 0.2.
P (D | B) = 0.5.
Menggunakan nilai -nilai ini, anda juga boleh menentukan kebarangkalian aksesori peristiwa -peristiwa ini, iaitu:
P (e | a) = 1 - p (d | a)
= 1 - 0.2
= 0.8
dan
P (e | b) = 1 - p (d | b)
= 1 - 0.5
= 0.5.
Sekarang, acara D boleh ditulis seperti berikut:
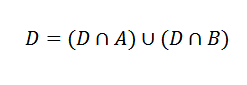 Acara ini saling eksklusif.
Acara ini saling eksklusif.
Menggunakan teorem pendaraban untuk kebarangkalian bersyarat ialah:
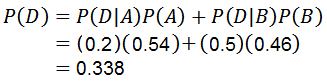
Yang mana soalan pertama dijawab.
Sekarang kita hanya perlu mengira P (A | D), yang mana teorem Bayes digunakan:
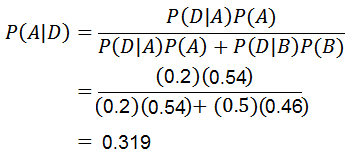
Terima kasih kepada Teorem Bayes, dapat mengesahkan bahawa kebarangkalian bahawa telefon bimbit telah dibuat oleh mesin A, mengetahui bahawa telefon bimbit itu cacat, adalah 0.319.
Boleh melayani anda: icosagonoLatihan 2
Tiga kotak mengandungi bola hitam dan hitam. Komposisi masing -masing adalah seperti berikut: u1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
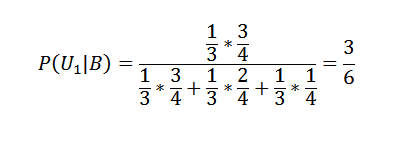
Salah satu kotak yang dipilih secara rawak dan bola rawak diekstrak daripadanya yang menjadi putih. Apakah kotak yang paling mungkin telah dipilih?
Penyelesaian
Melalui U1, U2 dan U3, kami juga akan mewakili kotak yang dipilih.
Peristiwa ini merupakan partition s dan disahkan bahawa p (u1) = p (u2) = p (u3) = 1/3 kerana pilihan kotak adalah rawak.
Jika b = bola yang diekstrak putih, kita akan mempunyai p (b | u1) = 3/4, p (b | u2) = 2/4, p (b | u3) = 1/4 .
Apa yang ingin kita peroleh adalah kebarangkalian bahawa bola telah diambil dari kotak IU mengetahui bahawa bola ini putih, iaitu, p (ui | b), dan melihat mana dari tiga nilai yang tertinggi untuk mengetahui yang mana Kotak mana yang lebih cenderung untuk pengekstrakan bola putih.
Memohon Teorem Bayes ke kotak pertama:
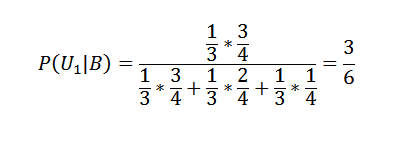
Dan untuk dua yang lain:
P (U2 | B) = 2/6 dan P (U3 | B) = 1/6.
Kemudian, kotak pertama adalah yang mempunyai kebarangkalian yang lebih besar untuk dipilih untuk pengekstrakan bola putih.