Teorem Bolzano

Kami menerangkan apa teorem Bolzano, aplikasinya dan meletakkan latihan yang diselesaikan

Apakah teorem Bolzano?

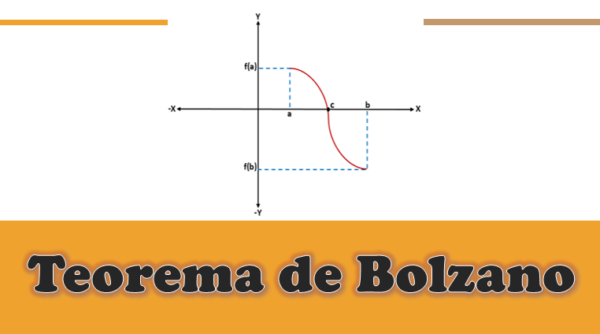
Dia Teorem Bolzano Ia menegaskan bahawa jika fungsi berterusan di semua titik selang tertutup [a, b] dan ia dipenuhi bahawa imej "a" dan "b" (di bawah fungsi) mempunyai tanda bertentangan, maka akan ada sekurang -kurangnya Satu titik "c" dalam selang terbuka (a, b), supaya fungsi yang dinilai dalam "c" akan sama dengan 0.

Teorem ini dinyatakan oleh ahli falsafah, ahli teologi dan ahli matematik Bernard Bolzano pada tahun 1850. Saintis ini, yang dilahirkan di Republik Czech semasa, adalah salah satu matematik pertama dalam sejarah untuk membuat demonstrasi rasmi sifat -sifat fungsi yang berterusan.

Penjelasan Teorem

Teorem Bolzano juga dikenali sebagai Teorem Nilai Pertengahan, yang membantu dalam menentukan nilai -nilai tertentu, terutamanya sifar, dari fungsi sebenar tertentu pembolehubah sebenar.

Dalam fungsi tertentu f (x) berterusan -iaitu, bahawa f (a) dan f (b) disambungkan oleh lengkung-, di mana f (a) berada di bawah paksi x (negatif), dan f (b) Dengan di atas paksi x (ia positif), atau sebaliknya, akan ada titik pemotongan pada paksi x yang akan mewakili nilai perantaraan "C", yang akan menjadi antara "A" dan "B", dan nilai f (c) ia akan sama dengan 0.

Apabila menganalisis teorem Bolzano secara grafik, dapat diketahui bahawa untuk sebarang fungsi F berterusan yang ditakrifkan dalam selang [a, b], di mana f (a)_*f (b) kurang daripada 0, akan ada sekurang -kurangnya satu akar "c" fungsi itu dalam selang waktu (a, b).

Teorem ini tidak menetapkan bilangan mata yang ada dalam selang terbuka, hanya menyatakan bahawa terdapat sekurang -kurangnya 1 mata.

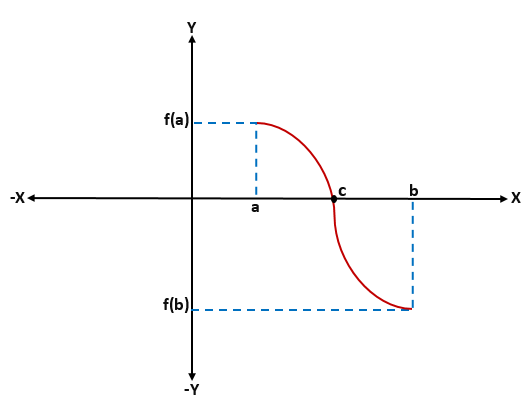
Demonstrasi Teorem Bolzano

Untuk menunjukkan teorem Bolzano, ia diandaikan tanpa kehilangan keluasan yang f (a) 0; Dengan cara ini, mungkin terdapat banyak nilai antara "a" dan "b" yang mana f (x) = 0, tetapi hanya perlu untuk menunjukkan bahawa ada satu.

Boleh melayani anda: Nombor khayalan: sifat, aplikasi, contoh

Ia mula menilai f pada titik tengah (a+b)/2. Jika f ((a+b)/2) = 0 maka ujian berakhir di sini; Jika tidak, F ((a+b)/2) positif atau negatif.

Salah satu bahagian selang [a, b] dipilih, sehingga tanda -tanda fungsi yang dinilai di hujungnya berbeza. Selang baru ini akan menjadi [A1, B1].

Sekarang, jika F dinilai pada titik tengah [A1, B1] tidak sifar, maka operasi yang sama dilakukan sebelum ini; Iaitu, separuh daripada selang ini yang memenuhi syarat tanda -tanda dipilih. Jadilah selang baru ini [A2, B2].

Jika proses ini berterusan, maka akan ada dua penggantian an dan bn, seperti itu:

an berkembang dan bn berkurangan:

A ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. . ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Jika panjang setiap selang [AI, BI] dikira, anda perlu:

B1-A1 = (B-A)/2.

B2-A2 = (B-A)/2².

… .

bn-an = (b-a)/2^n.

Oleh itu, had apabila n cenderung kepada tak terhingga (bn-an) sama dengan 0.

Menggunakan an semakin meningkat dan terhad dan bn berkurangan dan terhad, terdapat nilai "c" seperti itu:

A ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. .≤ c ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Had LIM ialah "C" dan had Bn juga "C". Oleh itu, diberi δ> 0, selalu ada "n" sehingga selang [AN, bn] terkandung dalam selang (c-δ, c+δ).

Sekarang, mesti ditunjukkan bahawa f (c) = 0.

Jika f (c)> 0, maka sebagai f berterusan, terdapat ε> 0 sehingga f positif sepanjang selang (c -ε, c+ε). Walau bagaimanapun, seperti yang dinyatakan di atas, terdapat nilai "n" sedemikian rupa sehingga perubahan f masuk [an, bn] dan, sebagai tambahan, [an, bn] terkandung dalam (c -ε, c+ε), apa yang ada percanggahan.

Jika f (c) 0 supaya f negatif sepanjang selang (c -ε, c+ε); Tetapi ada nilai "n" yang f berubah log masuk [AN, bn]. Ternyata [AN, BN] terkandung dalam (c -ε, c+ε), yang juga percanggahan.

Boleh melayani anda: tanda -tanda kumpulan

Oleh itu, f (c) = 0 dan inilah yang ingin ditunjukkan.

Apa teorem Bolzano?

Dari tafsiran grafiknya, teorem Bolzano digunakan untuk mencari akar atau sifar dalam fungsi yang berterusan, melalui bisensi (pendekatan), yang merupakan kaedah carian tambahan yang selalu membahagikan selang menjadi 2.

Oleh itu, jika perubahan fungsi menandatangani selang, fungsi F dinilai pada titik tengah, yang dinyatakan seperti berikut: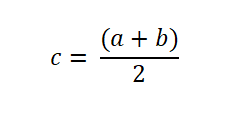Akar dijumpai apabila f (c) = 0. Jika tidak, tanda f (c) dianalisis untuk menentukan sama ada ia menentang tanda f (a) atau f (b).

Kemudian selang [A, C] atau [C, B] diambil di mana perubahan tanda berlaku, dan prosesnya diulang sehingga selang waktu kurang dan kurang, untuk mendekati nilai yang anda inginkan; iaitu, dengan nilai fungsi itu dilakukan 0.

Ringkasnya, untuk memohon teorem Bolzano dan dengan itu mencari akar, hadkan sifar fungsi atau memberi penyelesaian kepada persamaan, langkah -langkah berikut dilakukan:

1. Ia disahkan jika f adalah fungsi berterusan dalam selang [a, b].
2. Sekiranya selang tidak diberikan, seseorang mesti mencari satu fungsi di mana berterusan.
3. Ia disahkan jika hujung selang memberikan tanda bertentangan apabila dinilai dalam f.
4. Sekiranya tanda bertentangan tidak diperoleh, selang mesti dibahagikan kepada dua subinterval menggunakan titik tengah.
5. Menilai fungsi di titik tengah dan mengesahkan bahawa hipotesis Bolzano dipenuhi, di mana f (a) _* f (b) < 0.
6. Bergantung pada tanda (positif atau negatif) nilai yang dijumpai, prosesnya diulang dengan subinterval baru sehingga hipotesis yang disebutkan dipenuhi.

Boleh melayani anda: Pengaturcaraan bukan linear: Kaedah dan Latihan

Latihan yang diselesaikan

Latihan 1

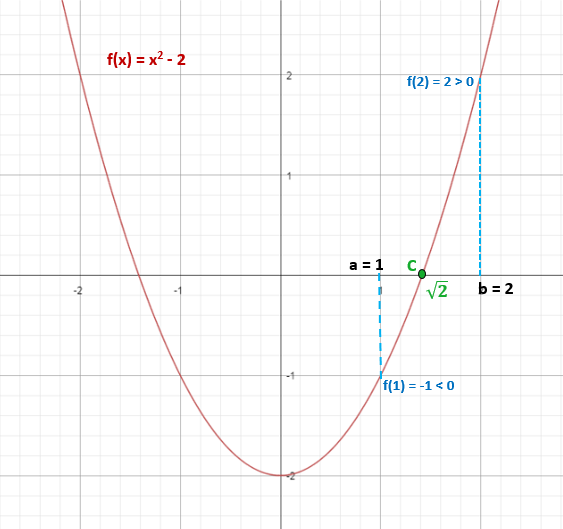
Tentukan sama ada fungsi f (x) = x² - 2, mempunyai sekurang -kurangnya satu penyelesaian sebenar dalam selang waktu [1,2].

Penyelesaian

Anda mempunyai fungsi f (x) = x² - 2. Seperti polinomial, ini bermakna ia berterusan dalam selang waktu.

Diminta untuk menentukan sama ada ia mempunyai penyelesaian sebenar dalam selang waktu [1, 2], jadi sekarang anda hanya perlu menggantikan hujung selang dalam fungsi untuk mengetahui tanda ini dan tahu jika mereka memenuhi syarat menjadi berbeza:

f (x) = x² - 2

F (1) = 1² - 2 = -1 (negatif)

F (2) = 2² - 2 = 2 (positif)

Oleh itu, tanda f (1) ≠ tanda f (2).

Ini memastikan bahawa terdapat sekurang -kurangnya satu titik "C" yang dimiliki oleh selang [1,2], di mana f (c) = 0.

Dalam kes ini, nilai "C" boleh dikira dengan mudah seperti berikut:

x² - 2 = 0

x = ± √2.

Oleh itu, √2 ≈ 1.4 tergolong dalam selang [1,2] dan memenuhi bahawa f (√2) = 0.

Latihan 2

Menunjukkan bahawa persamaan x⁵ + x + 1 = 0 mempunyai sekurang -kurangnya satu penyelesaian sebenar.

Penyelesaian

Mula -mula kita perhatikan bahawa f (x) = x⁵ + X + 1 adalah fungsi polinomial, yang bermaksud bahawa ia berterusan dalam semua nombor sebenar.

Dalam kes ini, tiada selang diberikan, jadi anda mesti memilih nilai secara intuitif, sebaiknya hampir 0, untuk menilai fungsi dan mencari perubahan tanda:

Jika selang [0, 1] digunakan, ia perlu:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

F (1) = 1⁵ + 1 + 1 = 3> 0.

Oleh kerana tidak ada perubahan tanda, prosesnya diulang dengan selang waktu yang lain.

Jika selang [-1, 0] digunakan, anda perlu:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

Dalam selang ini terdapat perubahan tanda: tanda f (-1) ≠ tanda f (0), yang bermaksud bahawa fungsi f (x) = x⁵ + X + 1 mempunyai sekurang-kurangnya satu akar sebenar "c" dalam selang [-1, 0], seperti f (c) = 0. Dengan kata lain, memang benar bahawa x⁵ + x + 1 = 0 mempunyai penyelesaian sebenar dalam selang [-1,0].