Penjelasan Teorem Overlay, Aplikasi, Latihan Diselesaikan

Dia Teorem Superposition, Dalam litar elektrik, ia menetapkan bahawa voltan antara dua titik, atau arus melalui mereka, adalah jumlah algebra voltan (atau arus jika ia adalah kes), kerana setiap sumber, seolah -olah setiap satu bertindak dalam a cara bebas.

Teorem ini membolehkan menganalisis litar linear yang mengandungi lebih daripada satu sumber bebas, kerana hanya perlu untuk mengira sumbangan masing -masing secara berasingan.

Ketergantungan linear adalah tegas bagi teorem untuk memohon. Litar linear adalah tindak balasnya yang berkadar terus dengan entri.

Sebagai contoh, undang -undang Ohm digunakan untuk rintangan elektrik menetapkan bahawa V = i.R, di mana V Ia adalah voltan, R adalah rintangan dan Yo Ia adalah semasa. Ia kemudiannya bergantung pada voltan dan arus dalam rintangan.

Dalam litar linear, prinsip superposisi digunakan dengan mengambil kira perkara berikut:

-Setiap sumber voltan bebas mesti dipertimbangkan secara berasingan dan untuk ini adalah perlu untuk mematikan semua yang lain. Sudah cukup untuk meletakkan 0 V semua yang tidak dianalisis atau menggantikannya dalam skim dengan litar pintas.

-Sekiranya sumbernya maka litar mesti dibuka.

-Apabila rintangan dalaman kedua -dua sumber semasa dan voltan dipertimbangkan, ini mesti kekal di tempat, menjadi sebahagian daripada litar yang lain.

-Sekiranya terdapat sumber yang bergantung, mereka mesti muncul di litar.

[TOC]

Aplikasi

Teorem bertindih digunakan untuk mendapatkan litar yang lebih mudah dan lebih mudah untuk dikendalikan. Tetapi ia harus diingat bahawa hanya berlaku kepada mereka yang mempunyai respons linear, seperti yang dinyatakan pada awalnya.

Kemudian ia tidak boleh digunakan secara langsung untuk mengira kuasa misalnya, kerana kuasa itu berkaitan dengan arus melalui:

P = i² R

Oleh kerana arus itu dikuangkan, jawapannya tidak linear. Juga tidak terpakai bagi litar magnet di mana transformer campur tangan.

Boleh melayani anda: elektrik dinamik

Sebaliknya, teorem superposisi memberi peluang untuk mengetahui kesan setiap sumber di litar. Dan tentu saja, melalui aplikasinya adalah mungkin untuk menyelesaikannya sepenuhnya, iaitu, untuk mengetahui arus dan voltan melalui setiap rintangan.

Teorem bertindih juga boleh digunakan bersempena dengan teorem litar lain, contohnya Thévenin, untuk menyelesaikan konfigurasi yang lebih kompleks.

Dalam litar semasa berselang, teorem juga berguna. Dalam kes ini, kami bekerja dengan impedans dan bukannya rintangan, selagi jumlah tindak balas setiap kekerapan bebas dapat dikira.

Akhirnya, dalam sistem elektronik, teorem boleh digunakan untuk analisis semasa langsung dan alternatif, secara berasingan.

Langkah -langkah untuk Memohon Teorem Bertindih

-Menyahaktifkan semua sumber bebas mengikut arahan yang diberikan pada mulanya, kecuali yang dianalisis.

-Tentukan output, sama ada voltan atau arus, yang menghasilkan sumber tunggal itu.

-Ulangi dua langkah yang diterangkan untuk semua sumber lain.

-Kirakan jumlah algebra dari semua sumbangan yang terdapat pada langkah -langkah sebelumnya.

Latihan yang diselesaikan

Contoh -contoh yang diselesaikan di bawah menjelaskan penggunaan teorem dalam beberapa litar sederhana.

- Contoh 1

Dalam litar yang ditunjukkan dalam angka berikut, cari arus yang melintasi setiap rintangan melalui teorem bertindih.

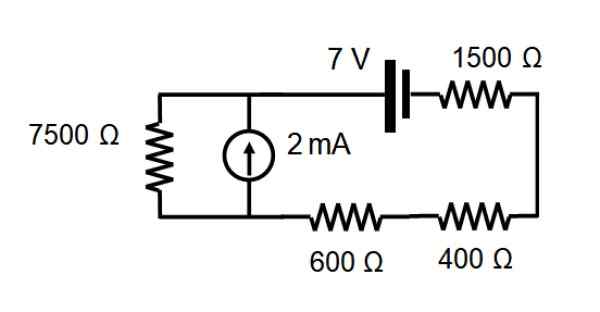
Penyelesaian

Sumbangan sumber voltan

Untuk memulakan sumber semasa dihapuskan, dengan mana litar tetap dengan cara ini:

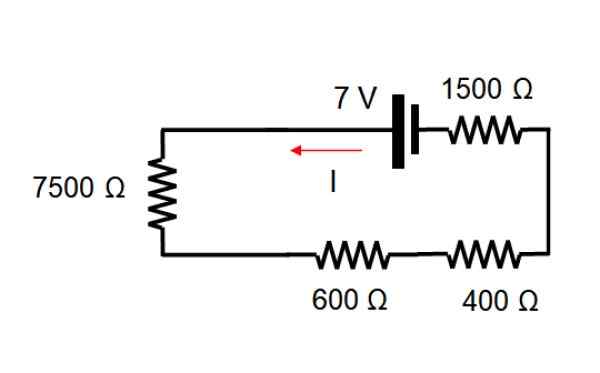
Rintangan bersamaan adalah menambah nilai setiap rintangan, kerana mereka semua dalam siri:

7500 +600 +400 +1500 Ω = 10.000 Ω

Memohon undang -undang ohm V = i.R Dan membersihkan arus:

I = v / r = 7/10.000 a = 0.0007 a = 0.7 ma

Arus ini sama untuk semua rintangan.

Boleh melayani anda: Eksperimen Millikan: Prosedur, Penjelasan, Kepentingan

Sumbangan sumber semasa

Sumber voltan segera dihapuskan, hanya berfungsi dengan sumber semasa. Litar yang dihasilkan ditunjukkan di bawah:

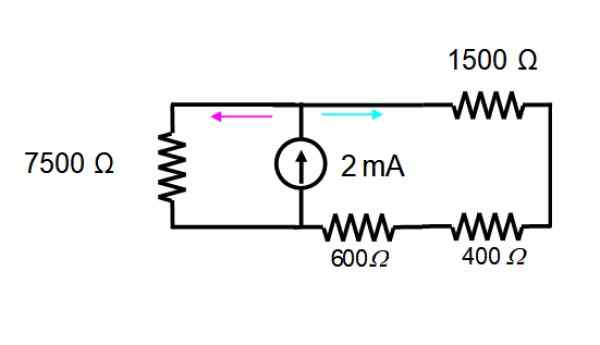
Rintangan dalam mesh di sebelah kanan adalah siri dan boleh digantikan dengan hanya satu:

600 +400 + 1500 Ω = 2500 Ω

Litar yang dihasilkan seperti ini:

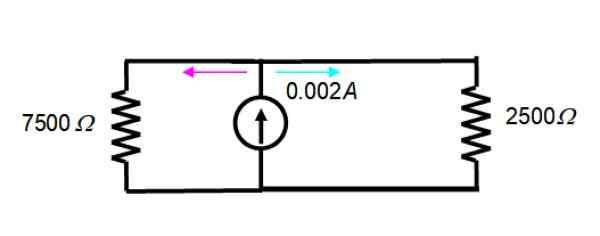
Arus 2 ma = 0.002 A dibahagikan antara kedua -dua rintangan angka, oleh itu persamaan pembahagi semasa adalah sah:

Yo_x = (R_Pers/R_x) Yo_T

Di mana Yo_x Adakah semasa dalam rintangan R_x, R_Pers melambangkan rintangan setara dan Yo_T adalah jumlah semasa. Adalah perlu untuk mencari rintangan yang setara di antara mereka, mengetahui bahawa:

1/r_Pers = (1/ r₁) + (1/ r₂)

Oleh itu:

1/r_Pers = (1/7500) + (1/2500) = 1/1875 → R_Pers = 1875 Ω

Untuk litar lain ini, arus yang melewati rintangan 7500 Ω menggantikan nilai dalam persamaan pembahagian semasa:

Yo_{7500 Ω} = (1875/7500). 0.002 a = 0.0005 a = 0.5 ma

Manakala yang melewati rintangan 2500 Ω adalah:

Yo_{2500 Ω} = 2 ma - 0.5 ma = 1.5 ma

Permohonan Teorem Superposition

Sekarang teorem bertindih untuk setiap rintangan digunakan, bermula dengan 400 Ω:

Yo_{400 Ω} = 1.5 ma - 0.7 ma = 0.8 ma

Penting: Untuk rintangan ini, arus dikurangkan, kerana mereka beredar ke arah yang bertentangan, seperti yang dapat dilihat dari pemerhatian yang teliti terhadap angka -angka, di mana deria arus mempunyai warna yang berbeza.

Arus yang sama ini sama rata dengan rintangan 1500 Ω dan 600 Ω, kerana mereka semua dalam siri.

Kemudian teorem digunakan untuk mencari arus melalui rintangan 7500 Ω:

Yo_{7500 Ω} = 0.7 ma + 0.5 ma = 1.2 ma

Penting: Sekiranya rintangan 7500 Ω, perhatikan bahawa arus ditambah, kerana dalam kedua -dua litar mereka beredar ke arah yang sama ketika melewati rintangan ini. Sekali lagi adalah perlu untuk memerhatikan dengan teliti deria arus.

Boleh melayani anda: ralat relatif: formula, bagaimana ia dikira, latihan

- Latihan 2

Cari arus dan voltan melalui rintangan 12 Ω melalui teorem tumpang tindih.

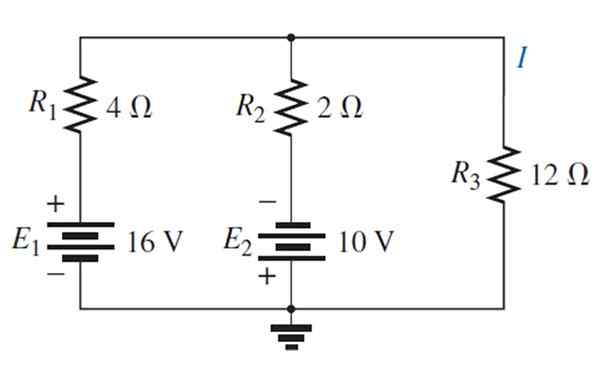
Penyelesaian

Sumber e diganti₁ Dengan litar pintas:

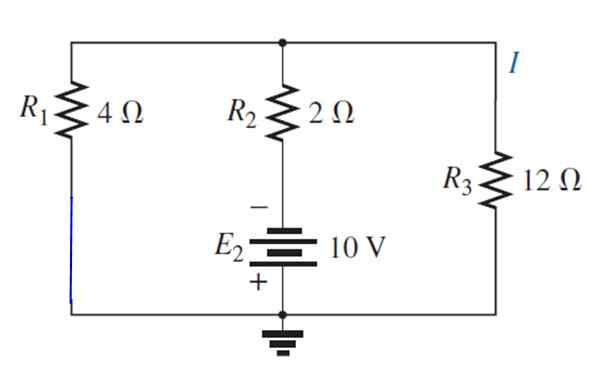
Litar yang dihasilkan ditarik seperti berikut, dengan mudah menggambarkan perintang yang kekal selari:

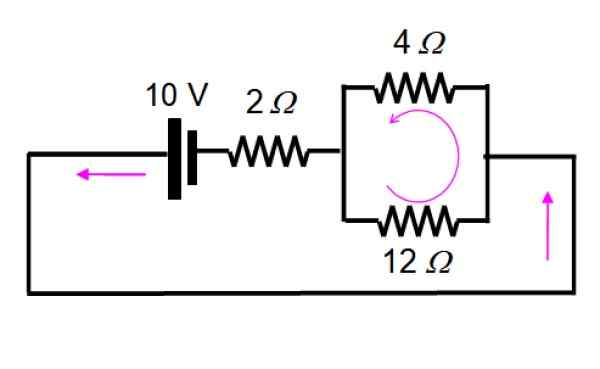
Dan sekarang ia diselesaikan dengan menggunakan siri dan selari:

1/r_Pers = (1/12) + (1/4) = 1/3 → R_Pers = 3 Ω

Rintangan ini pada gilirannya dengan siri dengan 2 Ω, Oleh itu jumlah rintangan adalah 5 Ω. Jumlah arus adalah:

I = v / r = 10 v / 5 Ω = 2 a

Arus ini dibahagikan sebagai:

Yo_12Ω = (3/12) 2 a = 0.5 a

Oleh itu voltan adalah:

V_12Ω = 0.5 a × 12 Ω = 6 v

Sekarang sumbernya diaktifkan₁:

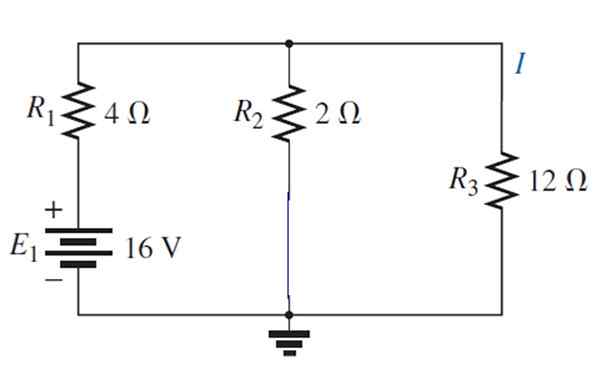
Litar yang dihasilkan boleh ditarik dengan cara ini:

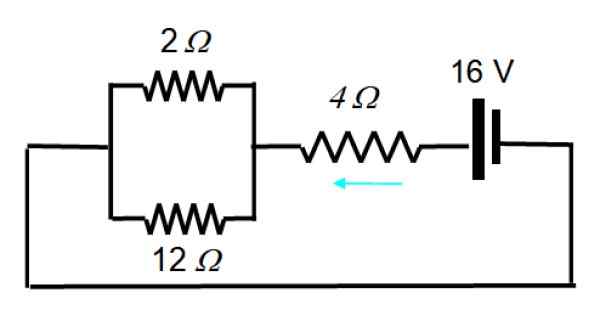
1/r_Pers = (1/12) + (1/2) = 7/12 → R_Pers = 12/7 Ω

Dan dalam siri dengan 4 Ω Ia adalah rintangan yang setara 40/7 Ω. Dalam kes ini jumlah arus adalah:

I = v/r = 16 v/(40/7) Ω = 14/5 a

Pembahagi voltan dengan nilai -nilai ini digunakan lagi:

Yo_12Ω = ((12/7)/12) (14/5) a = 0.4 a

Arus yang dihasilkan adalah: 0.lima puluh.4 a = 0.1 a. Perhatikan bahawa mereka telah dikurangkan, kerana arus setiap sumber membuat makna yang berbeza, seperti yang dapat dilihat di litar asal.

Voltan melalui rintangan adalah:

V_12Ω = 0.4 a × 12 Ω = 4.8 v

Akhirnya, jumlah voltan adalah: 6 V-4.8 V = 1.2 v

Rujukan

1. Alexander, c. 2006. Asas Litar Elektrik. Ke -3. Edisi. MC Graw Hill.
2. Boylestad, r. 2011. Pengenalan kepada Analisis Litar. 2. Edisi. Pearson.
3. Dorf, r. 2006. Pengenalan kepada litar elektrik. Ke -7. Edisi. John Wiley & Sons.
4. Edminister, j. Sembilan belas sembilan puluh enam. Litar elektrik. Siri Schaum. Ke -3. Edisi. MC Graw Hill
5. Wikipedia. Pembahagi semasa. Pulih dari: ia adalah.Wikipedia.org.