Sifat matriks ortogonal, demonstrasi, contoh

Awak ada satu Matriks Orthogonal Ketika dikatakan matriks didarab dengan hasil transposnya dalam matriks identiti. Sekiranya songsang matriks sama dengan yang dipindahkan maka matriks asal adalah ortogonal.

Matriks ortogonal adalah ciri bahawa bilangan baris adalah sama dengan bilangan lajur. Di samping itu, vektor baris adalah vektor ortogonal unit dan ruam vektor yang ditransposikan juga.

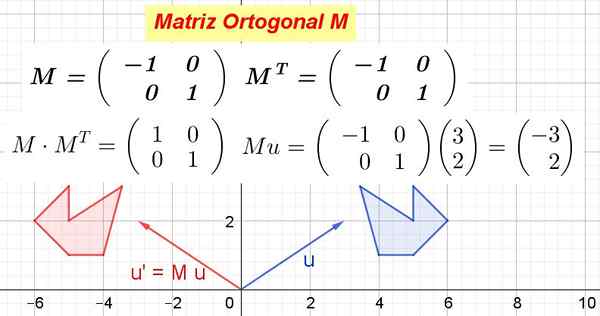Rajah 1. Contoh matriks ortogonal dan bagaimana mengubah objek geometri. (Disediakan oleh Ricardo Pérez)

Apabila matriks ortogonal didarabkan oleh vektor ruang vektor menghasilkan a transformasi isometrik, iaitu, transformasi yang tidak mengubah jarak dan mengekalkan sudut.

Wakil biasa matriks ortogonal adalah Matriks putaran. Transformasi matriks ortogonal pada ruang vektor dipanggil Transformasi Orthogonal.

Transformasi geometri putaran dan refleksi titik yang diwakili oleh vektor kartesinya dibuat dengan menggunakan matriks ortogonal pada vektor asal untuk mendapatkan koordinat vektor yang diubah. Oleh sebab itu, matriks ortogonal digunakan secara meluas dalam pemprosesan grafik pengiraan.

[TOC]

Sifat

Array M Ia adalah ortogonal jika didarab dengan transposinya M^T matriks identiti menghasilkan Yo. Begitu juga, produk transpose matriks ortogonal oleh matriks asal matriks identiti:

M m^T = M^T M = i

Sebagai akibat dari pernyataan terdahulu, yang dipindahkan dari matriks ortogonal adalah sama dengan matriks songsang:

M^T = M^-1.

Set matriks dimensi ortogonal n x n Mereka membentuk kumpulan ortogonal Atau (n). Dan subset dari Atau (n) matriks ortogonal dengan menentukan +1 bentuk Kumpulan Matriks Khas ITS (n). Matriks kumpulan Anda (n) Mereka adalah matriks yang menghasilkan transformasi putaran linear, juga dikenali sebagai Kumpulan putaran.

Demonstrasi

Kami akan menunjukkan bahawa matriks adalah ortogonal jika, dan hanya jika, vektor baris (atau vektor lajur) adalah ortogonal antara satu sama lain dan norma 1.

Boleh melayani anda: Teorem Bayes

Anggapkan bahawa pangkat matriks ortogonal n x n adalah vektor ortonormal dimensi n. Sekiranya ia dilambangkan oleh v1, v2,… ., vn Vektor n dipenuhi:

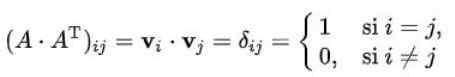
Di mana jelas bahawa set vektor baris adalah satu set vektor ortogonal dengan norma satu.

Contoh

Contoh 1

Tunjukkan bahawa matriks 2 x 2 yang mempunyai vektor dalam baris pertama V1= (-1 0) dan dalam baris kedua vektor V2= (0 1) adalah matriks ortogonal.

Penyelesaian: Matriks dibina M dan transposanya dikira M^T:

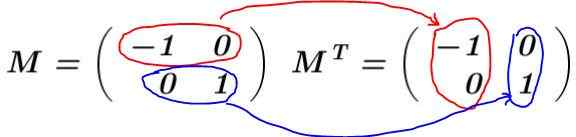
Dalam contoh ini, matriks M Ia adalah kereta yang dipindahkan, iaitu matriks dan transposinya adalah sama. Ia berlipat ganda M untuk transposinya M^T:

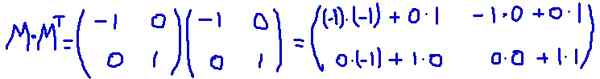
Ia disahkan bahawa M M^T Ia sama dengan matriks identiti:

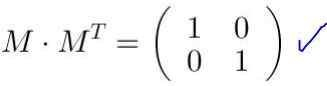
Apabila matriks M Ia didarabkan oleh koordinat vektor atau titik, koordinat baru diperolehi yang sesuai dengan transformasi yang dibuat oleh matriks pada vektor atau titik.

Rajah 1 menunjukkan bagaimana M Mengubah vektor atau dalam atau ' Dan juga suka M Mengubah poligon biru ke dalam poligon merah. Sebagai M Ia adalah ortogonal, ia adalah transformasi ortogonal, yang mengekalkan jarak dan sudut.

Contoh 2

Anggapkan bahawa anda mempunyai matriks 2 x 2 yang ditakrifkan dalam reais yang diberikan oleh ungkapan berikut:

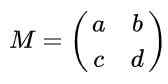
Cari nilai sebenar ke, b, c dan d Jadi matriks M Menjadi matriks ortogonal.

Penyelesaian: Secara definisi, matriks adalah ortogonal jika didarab dengan transposinya diperolehi sebagai hasilnya matriks identiti. Mengingat bahawa matriks yang dipindahkan diperoleh dari asal, bertukar baris mengikut lajur adalah kesamaan berikut:

Ia dapat melayani anda: domain dan percanggahan fungsi (dengan contoh)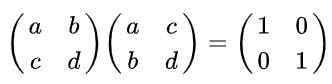

Melaksanakan pendaraban matriks adalah:

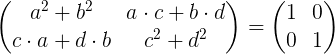
Menyamakan unsur -unsur matriks kiri dengan unsur -unsur matriks identiti di sebelah kanan, kami memperoleh sistem empat persamaan dengan empat tidak diketahui A, B, C dan D dan D.

Kami mencadangkan untuk A, B, C dan D ungkapan berikut berdasarkan sebab -sebab trigonometri sinus dan kosinus:

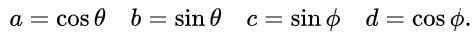
Dengan cadangan ini dan disebabkan oleh identiti trigonometri asas, persamaan pertama dan ketiga dalam kesamaan unsur -unsur matriks secara automatik berpuas hati. Persamaan ketiga dan keempat adalah sama dan dalam kesamaan matriks selepas menggantikan nilai yang dicadangkan adalah seperti ini:

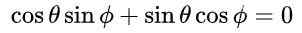
Yang membawa kepada penyelesaian berikut:

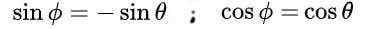
Akhirnya, penyelesaian berikut diperolehi untuk matriks ortogonal m:

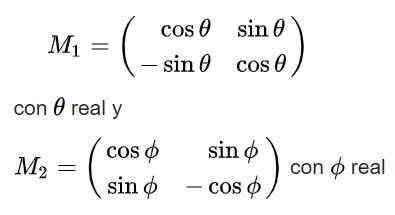
Perhatikan bahawa penyelesaian pertama mempunyai penentu +1 sehingga ia tergolong dalam kumpulannya (2), sementara penyelesaian kedua mempunyai penentu -1 dan oleh itu tidak tergolong dalam kumpulan ini.

Contoh 3

Memandangkan matriks berikut, cari nilai A dan B untuk mempunyai matriks ortogonal.

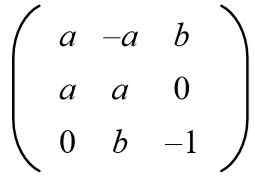
Penyelesaian: Untuk matriks yang diberikan menjadi ortogonal, produk dengan transposinya mestilah matriks identiti. Kemudian, produk matriks matriks yang diberikan dengan matriks yang dipindahkan dibuat memberikan hasil berikut:

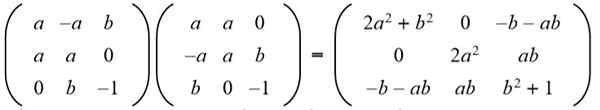
Seterusnya, hasilnya dipadankan dengan matriks identiti 3 x 3:

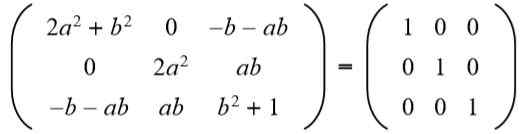
Dalam lajur ketiga baris kedua yang anda ada (A B = 0), tetapi ke Ia tidak boleh menjadi sifar, kerana jika ya, kesamaan unsur -unsur baris kedua dan lajur kedua tidak akan dipenuhi. Kemudian semestinya B = 0. Menggantikan b Untuk nilai 0 kita ada:

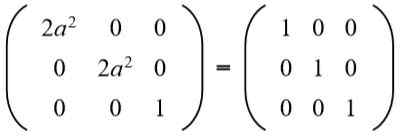
Kemudian persamaan diselesaikan: 2a^2 = 1, Penyelesaiannya ialah: +½√2 dan -½√2.

Boleh melayani anda: jenis sudut, ciri dan contoh

Mengambil penyelesaian positif untuk ke Ia menghasilkan matriks ortogonal berikut:

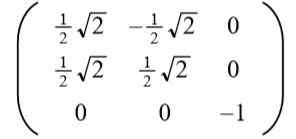
Pembaca dengan mudah dapat mengesahkan bahawa vektor baris (dan juga vektor lajur) adalah ortogonal dan unit, iaitu ortorormal.

Contoh 4

Menunjukkan bahawa matriks Ke yang barisnya V1 = (0, -1 0), V2 = (1, 0, 0) dan V3 = (0 0 -1) Ia adalah matriks ortogonal. Di samping itu, cari bagaimana vektor asas kanonik berubah I j k Kepada vektor U1, U2 dan U3.

Penyelesaian: Harus diingat bahawa elemen (i, j) matriks yang didarab dengan transposinya, adalah produk skalar vektor baris (i) oleh lajur (j) transpose. Di samping itu, produk ini sama dengan delta Kronecker sekiranya matriks adalah ortogonal:

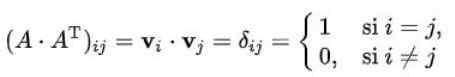
Dalam kes kita seperti ini:

V1 • V1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • v2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

Dengan apa yang menunjukkan bahawa ia adalah matriks ortogonal.

Selain u1 = a i = (0, 1, 0); U2 = j = (-1, 0, 0) dan akhirnya U3 = a k = (0, 0, -1)

Rujukan

1. Anthony Nicolaides (1994) Penentu & Matriks. Lulus penerbitan.
2. Birkhoff dan Maclane. (1980). Algebra moden, ed. Vicens-Vives, Madrid.
3. Casteleiro Villalba m.  (2004) Pengenalan kepada aljabar linear. Editorial ESIC.
4. Dave Kirkby (2004) Matematik Menyambung. Heinemann.
5. Jenny Olive (1998) Matematik: Panduan Survival Pelajar. Cambridge University Press.
6. Richard J. Brown (2012) Matematik 30 saat: 50 Teori Paling Minda yang Paling Minda dalam Matematik. Ivy Press Limited.
7. Wikipedia. Matriks Orthogonal. Pulih dari: Adakah.Wikipedia.com
8. Wikipedia. Matriks Orthogonal. Diperoleh dari: dalam.Wikipedia.com