Teorem Varignon

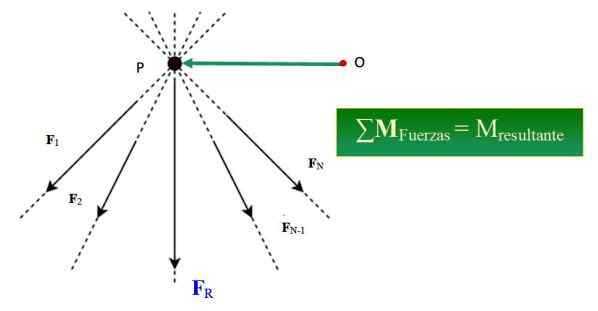
Rajah 1.- Teorem Varignon menegaskan bahawa jumlah momen kuasa di sekitar titik tertentu bersamaan dengan masa hasilnya berkenaan dengan titik itu. Sumber: Wikimedia Commons/F. Zapata.

Apa itu Teorem Varignon?

Teorem Varignon, dalam Mekanik, menyatakan bahawa jumlah momen yang dihasilkan oleh sistem kuasa serentak berkenaan dengan titik tertentu, adalah sama dengan momen daya yang dihasilkan berkenaan dengan titik yang sama.

Atas sebab ini teorem ini juga dikenali sebagai Permulaan momen.

Walaupun yang pertama menyatakan ia adalah orang Belanda Simon Stevin (1548-1620), pencipta paradoks hidrostatik, ahli matematik Perancis Pierre Varignon (1654-1722) adalah orang yang kemudiannya memberinya bentuk definitifnya.

Contoh bagaimana teorem Varignon berfungsi dalam mekanik adalah seperti berikut: Katakan bahawa sistem mudah dua coplanar dan daya serentak bertindak pada satu titik F₁ dan F₂, (Dilambangkan dengan berani untuk watak vektornya). Daya ini menimbulkan kekuatan bersih atau yang dihasilkan, yang dipanggil F_R.

Setiap daya menghasilkan tork atau momen berkenaan dengan titik atau, yang dikira oleh produk vektor antara vektor kedudukan r_Op dan strengh F, di mana r_Op Ia diarahkan dari atau ke titik persetujuan p:

M_O1 = r_Op × F₁

M_O2 = r_Op × F₂

Diberi F_R = F₁ + F₂, Jadi:

M_{Sama ada} = r_Op × F₁ + r_Op × F₂ = M_O1 + M_O2

Tetapi bagaimana r_Op Ini adalah faktor yang sama, kemudian, menggunakan harta pengedaran kepada produk silang:

M_{Sama ada} = r_Op × (F₁ + F₂) = r_Op × F_R                

Oleh itu, jumlah momen atau tork setiap daya berkenaan dengan titik atau bersamaan dengan masa daya yang terhasil berkenaan dengan titik yang sama.

Pernyataan dan demonstrasi

Menjadi sistem kuasa serentak, dibentuk oleh F₁, F₂, F₃… F_N, garis tindakan yang dimaksudkan pada titik p (lihat Rajah 1), saat sistem daya ini M_{Sama ada}, Mengenai titik atau diberikan oleh:

Boleh melayani anda: keseimbangan yang tidak stabil: konsep dan contoh

M_{Sama ada} = r_Op × F₁ + r_Op × F₂ + r_Op × F₃ +… r_Op × F_N = r_Op × (F₁ + F₂ + F₃ +… F_N)

Demonstrasi

Untuk menunjukkan teorem, harta pengedaran produk vektor antara vektor dibuat.

Menjadi kuasa F₁, F₂, F₃… F_N diterapkan pada mata ke₁, Ke₂, Ke₃... ke_N dan serentak pada titik p. Momen sistem ini yang terhasil, berkenaan dengan titik atau, dipanggil M_{Sama ada}, Ia adalah jumlah momen setiap daya, berkenaan dengan perkara itu:

M_{Sama ada} = Σ r_Oai × F_Yo

Di mana jumlahnya dari i = 1 hingga i = n, kerana ada kekuatan n. Oleh kerana ini adalah daya serentak dan sejak produk vektor antara vektor selari adalah batal, ia berlaku:

r_Pai × F_Yo = 0

Dengan vektor null dilambangkan sebagai 0.

Momen salah satu kuasa mengenai o, contohnya kekuatan F_Yo digunakan dalam a_Yo, Ia ditulis seperti ini:

M_{saya dengar} = r_Oai × F_Yo

Vektor kedudukan r_Oai  Ia boleh dinyatakan sebagai jumlah dua kedudukan vektor:

r_Oai = r_Op + r_Pai

Dengan cara ini, saat ini berkenaan dengan atau memaksa F_Yo adalah:

M_{saya dengar} = (r_Op + r_Pai) × F_Yo = (r_Op × F_Yo) + (r_Pai × F_Yo)

Tetapi istilah terakhir adalah batal, seperti yang dijelaskan di atas, kerana r_Pai berada dalam garis tindakan F_Yo, Oleh itu:

M_{saya dengar} = r_Op × F_Yo

Mengetahui bahawa momen sistem berkenaan dengan titik atau adalah jumlah semua momen individu setiap daya berkenaan dengan titik itu, maka:

M_{Sama ada} = Σ M_{saya dengar} = Σ r_Op × F_Yo

Sebagai r_Op Ia tetap keluar dari jumlah:

M_{Sama ada} = r_Op × (Σ F_Yo)

Tetapi Σ F_Yo Ia hanyalah bersih atau kekuatan yang dihasilkan F_R, Oleh itu, ia segera membuat kesimpulan bahawa:

Boleh melayani anda: Botol Leyden: Bahagian, Operasi, Eksperimen

M_{Sama ada} = r_Op × F_R

Contoh

Teorem Varignon memudahkan pengiraan momen daya F Mengenai titik atau struktur yang ditunjukkan dalam angka tersebut, jika daya dipecahkan ke dalam komponen segi empat tepatnya dan momen masing -masing dikira:

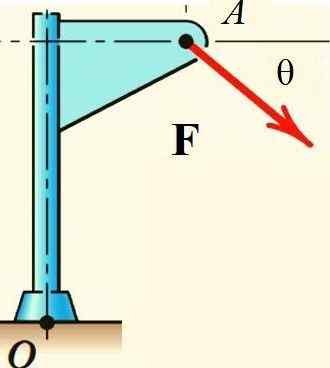Rajah 2.- Teorem Varignon terpakai untuk mengira momen daya di sekitar atau. Sumber: f. Zapata.

Aplikasi Teorem Varignon

Apabila daya yang terhasil daripada sistem diketahui, teorem Varignon boleh digunakan untuk menggantikan jumlah setiap momen yang dihasilkan oleh kekuatan yang mengarangnya pada masa yang dihasilkan.

Sekiranya sistem terdiri daripada daya pada satah yang sama dan titik berkenaan dengan mana yang anda ingin mengira momen milik pesawat itu, momen yang terhasil adalah tegak lurus.

Sebagai contoh, jika semua daya berada dalam satah XY, saat ini diarahkan pada paksi z dan hanya kekal untuk mencari magnitudnya dan maknanya, seperti halnya contoh yang diterangkan di atas.

Dalam hal ini, teorem Varignon membolehkan untuk mengira momen yang terhasil daripada sistem melalui penjumlahan. Ia sangat berguna dalam kes sistem daya tiga dimensi, yang mana arah momen yang terhasil tidak diketahui sebagai priori.

Untuk menyelesaikan latihan ini, ia adalah mudah.

Latihan diselesaikan

Oleh teorem Varignon, hitung momen daya F di sekitar titik atau ditunjukkan dalam angka jika magnitud f ialah 725 n.

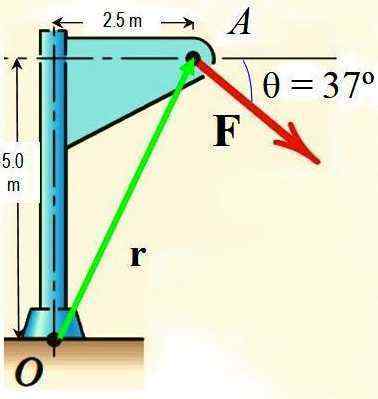Rajah 3.- Gambar untuk latihan yang diselesaikan. Sumber: f. Zapata.

Penyelesaian

Untuk memohon teorem Varignon, memaksa penguraian F Dalam dua komponen, yang momen masing -masing di sekitar atau dikira dan ditambah untuk mendapatkan momen yang terhasil.

Boleh melayani anda: badan tegar

F_x = 725 N ∙ cos 37 º = 579.0 n

F_dan = - 725 n n ∙ sen 37 º = -436.3 n

Begitu juga, vektor kedudukan r diarahkan dari atau ke A mempunyai komponen:

r_x = 2.5m

r_dan = 5.0 m

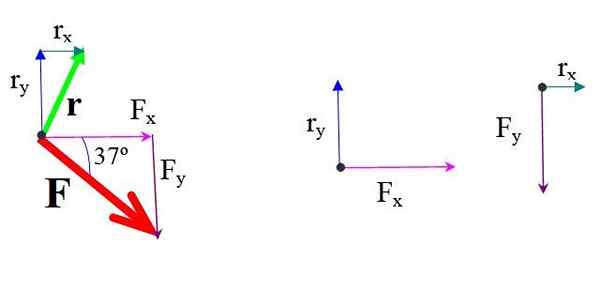Rajah 4.- Komponen daya dan kedudukan. Sumber: f. Zapata.

Momen setiap komponen daya berkenaan dengan atau mengalikan kekuatan dan jarak tegak lurus.

Kedua -dua kuasa cenderung untuk memutar struktur dalam arah yang sama, yang dalam kes ini adalah pengertian skor, yang sewenang -wenangnya diberikan tanda positif:

M_Lembu = F_x∙ r_dan ∙ Sin 90º = 579.0 n ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_dan∙ r_x ∙ dosa (-90º) = -436.3 n ∙ 2.5 m ∙ (-1) = 1090.8 n ∙ m

Momen yang dihasilkan berkenaan dengan atau adalah:

M_{Sama ada} = M_Lembu + M_Oy = 3985.8 n ∙ m tegak lurus ke satah dan dalam tork.

Rujukan

1. Bedford, 2000. Ke. Mekanik untuk Kejuruteraan: Statik. Addison Wesley. 
2. Bir, f. 2010. Statik. McGraw Hill. 9NA. Edisi.
3. Hibbeler, R. 1992. Mekanik untuk jurutera. 6th. Edisi. Cecsa.
4. Kejuruteraan HK. Teorem Varignon. Pulih dari: youtube.com.
5. Wikipedia. Teorem Varignon (Mekanik). Diperoleh dari: dalam.Wikipedia.org.