Teorem Faktor Penjelasan, Contoh, Latihan

Dia Teorem Faktor menyatakan bahawa polinomial p (x) boleh dibahagikan dengan binomial bentuk (x - a) jika x = a adalah akar p (x), iaitu p (a) = 0. Dikatakan bahawa polinomial dapat dibahagikan antara yang lain ketika sisa atau rehatnya adalah sifar.

Polinomial adalah ungkapan bentuk:

P (x) = a_n xⁿ + ke_N-1 x^N-1 +... + a₁ x + a₀

Rajah 1. Teorem Faktor. Sumber: f. Zapata.

Di mana:

-n adalah tahap polinomial, menjadi nombor integer terbesar yang mana pembolehubah bebas x meningkat,

-Nilai a_n, ke_N-1 ,... + a₁ , ke₀ Mereka adalah koefisien polinomial, yang umumnya nombor sebenar, tetapi mereka juga boleh menjadi bilangan kompleks.

Polinomial Gred N boleh terurai sebagai produk binomial bentuk:

(X - r_Yo)

Di mana r_Yo Ia adalah akar p (x) i-alkich:

P (x) = a_n (X - r₁) (X - r₂) ... (x - r_n)

Oleh kerana bilangan akar polinomial sama dengan tahap yang sama.

[TOC]

Contoh

- Contoh 1

Pertimbangkan polinomial mengikut kes:

P (x) = 3 ⋅x² - 7 ⋅x + 2

Anda ingin tahu sama ada polinomial ini boleh dibahagikan dengan binomial (x - 2). Sekiranya teorem faktor digunakan, maka kita mesti menilai p (x = 2) untuk mengetahui sama ada nilai 2 adalah akar atau tidak. Kami kemudiannya menilai ungkapan:

P (2) = 3 ⋅22 - 7 ⋅2 + 2 = 3 ⋅4 - 7 ⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.

Ternyata x = 2 adalah akar p (x), jadi menurut teorem faktor, binomial (x - 2) memang merupakan faktor p (x).

Mari beralih ke Pengesahan Langsung Membuat Bahagian. Perincian bagaimana bahagian dibuat ditunjukkan dalam angka berikut:

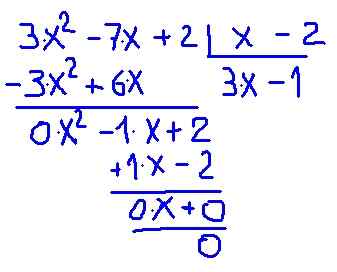Rajah 2.- Bahagian Polinomial P (x) antara binomial x-2. Sumber: f. Zapata.

Ia disahkan bahawa kuota antara p (x) dan (x -2) memberikan polinomial darjah kecil yang dipanggil quotient c (x) = 3 ⋅x - 1 dengan residu 0.

Boleh melayani anda: fungsi vektor

Kita boleh meringkaskan hasilnya seperti berikut:

(3 ⋅x² - 7 ⋅x + 2) ÷ (x -2) = (3 ⋅x - 1) + 0

Ekspresi sebelumnya boleh ditulis dengan cara lain, hanya ingat bahawa dividen p (x) adalah sama dengan produk pembahagi (x -2) oleh quotient (3 ⋅x - 1) ditambah sisa (sifar dalam kes ini ):

(3 ⋅x² - 7 ⋅x + 2) = (x -2) (3 ⋅x - 1) + 0

Dengan cara ini, polinomial p (x) (x), iaitu, menulis sebagai produk polinomial, polinomial asal: polinomial asal:

(3 ⋅x² - 7 ⋅x + 2) = (x -2) (3 ⋅x - 1)

- Contoh 2

Jadilah polinomial Q (x) = x³ - x + 2. Anda ingin tahu sama ada dibahagikan dengan binomial (x + 1).

Cara yang paling langsung adalah untuk menggunakan teorem faktor. Dalam kes ini, anda hanya perlu mengesahkan sama ada x = -1 menghidupkan atau tidak polinomial Q (x).

Kami meneruskan dengan menggantikan:

Q (-1) = (-1)³ - (-1) + 2 = -1 + 1 + 2 = 2

Hasilnya berbeza dari sifar, oleh itu faktor teorem memastikan bahawa polinomial q (x) tidak dapat dibahagikan antara (x + 1), kerana q (-1) ≠ ≠.

Sekarang pembahagian Q (x) akan dibuat antara binomial (x + 1) sebagai kaedah pengesahan kesimpulan kami.

Pada kesempatan ini, bahagian ini akan dijalankan melalui kaedah Bahagian Sintetik, yang terdiri daripada meletakkan di atas gred gred pertama di atas semua koefisien polinomial, termasuk yang hilang, kerana mereka mempunyai pekali sifar.

Kemudian dalam lajur pertama istilah bebas pembahagi diletakkan tetapi dengan tanda berubah, dalam kes kami pembahagi adalah (x + 1). Istilah bebasnya adalah 1, tetapi seperti dalam lajur pertama ia diletakkan tanda berubah, iaitu -1.

Angka berikut menggambarkan bagaimana bahagian sintetik dijalankan:

Boleh melayani anda: persamaan polinomial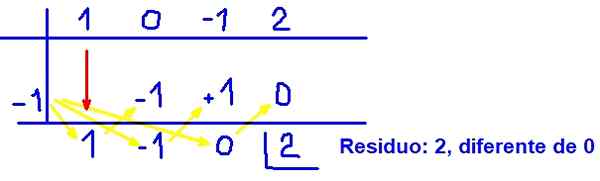Rajah 3. Contoh bahagian sintetik polinomial. Sumber: f. Zapata.

Dengan hasil ini terbukti bahawa (x + 1) ia bukan faktor polinomial q (x) = x³ - x + 2 kerana sisa tidak sifar.

Kesimpulan ini tidak terkejut, kerana ia telah diramalkan dengan teorem faktor. Perhatikan bahawa apabila menggantikan x = -1 dalam q (x) apa yang diperolehi adalah tepat sisa atau sisa bahagian polinomial, kerana q (-1) = residu = 2.

Sudah tentu, bahagian ini memberikan maklumat tambahan mengenai quotient c (x) = x² - x.

Mengingati bahawa dividen q (x) adalah sama dengan pembahagi (x + 1) dengan nisbah c (x) ditambah dengan residu r = 2 kita mempunyai pengembangan polinomial q (x) seperti berikut:

Q (x) = (x + 1) (x² - x) + 2 = x (x + 1) (x - 1) + 2

Harus diingat bahawa ungkapan ini bukanlah pemfaktoran polinomial tersebut, kerana terdapat penambahan istilah yang tidak null, yang tepatnya nilai nilai 2.

Latihan

- Latihan 1

Cari faktor polinomial

P (x) = x³ - 5 x² + 2 x + 8

Dan juga tulis pemfaktoran anda.

Penyelesaian

Teorem faktor menunjukkan bahawa kita mesti mencari akar ke Dan kemudian cari faktor (x - ke), Dalam kes ini, kerana ia adalah gred tiga polinomial, mesti ada tiga akar. 

Oleh kerana polinomial dengan keseluruhan koefisien, akar mestilah antara pembahagi istilah bebas yang dalam kes ini adalah 8. Pembahagi ini adalah:

± 1, ± 2, ± 4, ± 8.

Kami mulakan dengan meneroka +1: p (+1) = 1³ - 5 ⋅ 1² + 2 ⋅1 + 8 = 1 - 5 + 2 + 8 = 6 yang berbeza dari 0, oleh itu +1 bukan akar.

Kami meneroka -1:

P (-1) = (-1)³ - 5 ⋅ (-1)² + 2 ⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0

Dari hasilnya disimpulkan bahawa -1 adalah akar p (x) y (x -( -1)) = (x + 1) adalah faktor polinomial.

Boleh melayani anda: dataran minimum

Kita perlu mencari dua lagi faktor:

Kami mencuba yang seterusnya adalah +2:

P (+2) = (+2)³ - 5 ⋅ (+2)² + 2 ⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0

Sekali lagi kita mendapat sifar. Maka faktor lain adalah (x - 2).

Kerana ia adalah gred tiga polinomial kita hanya perlu mencari faktor. Sekarang kami mencuba nilai +4 untuk mengetahui sama ada polinomial membatalkan:

P (+4) = (+4)³ - 5 ⋅ (+4)² + 2 ⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.

Dalam kata lain.

Anda tidak perlu terus mencari, kerana ia adalah polinomial gred 3 yang mempunyai tiga akar paling banyak. Dalam latihan ini semua akar ternyata nyata dan keseluruhan.

Oleh itu polinomial P (x) adalah faktor seperti ini:

P (x) = x³ - 5 x² + 2 x + 8 = (x + 1) (x - 2) (x - 4).

- Latihan 2

Jadilah polinomial pip³ - x + 2p. Tentukan nilai P untuk polinomial yang boleh dibahagikan dengan (x + 2).

Penyelesaian

Kami menggunakan teorem faktor, yang menyatakan bahawa jika x = -2 membatalkan polinomial kemudian (x -( -2)) adalah faktor polinomial tersebut.

Kemudian x digantikan oleh (-2) dalam polinomial asal, ia dipermudahkan dan sama dengan sifar:

Pip (-2)³ - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0

Sekarang nilai p dibersihkan supaya kesamaan dipenuhi dengan sifar:

P = -2 / 10 = -⅕ 

Ini bermaksud polinomial: 

-⅕⋅x³ - X - ⅖

Ia boleh dibahagikan dengan (x + 2), atau yang setara: (x + 2) adalah salah satu faktornya.

Rujukan

1. Baldor Aurelio. Algebra. Kumpulan Editorial Patria.
2. Demana, w. Precáculculo: grafik, berangka, algebra ke -7 ed. Pendidikan Pearson.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.