Jenis segitiga

Klasifikasi segitiga

Segitiga adalah poligon atau angka geometri yang mempunyai tiga sisi, tiga simpang dan tiga sudut. Sisi adalah setiap garis lurus yang membentuknya. Tangkai adalah titik di mana sisi disatukan; Sudut adalah gerbang atau bukaan yang terbentuk berhampiran simpang, dengan menyertai dua sisi.

Segitiga juga boleh ditakrifkan sebagai kawasan yang ditentukan oleh tiga baris. Jumlah tiga sudutnya selalu sama dengan 180º. Panjang mana -mana sisinya selalu kurang daripada hasil jumlah panjang dua pihak yang lain, tetapi lebih besar daripada pengurangannya.

Segitiga adalah angka geometri yang paling mudah, dan berfungsi untuk menyiasat sifat matematik angka lain yang lebih kompleks, seperti pentagon atau heksagon.

Mereka juga digunakan dalam sains lain, seperti topografi, navigasi atau astronomi. Pada yang terakhir mereka digunakan untuk mengetahui jarak yang memisahkan kita dari badan biru muda yang jauh dari dua titik pemerhatian yang terletak di Bumi. Kaedah ini dikenali sebagai Parallage.

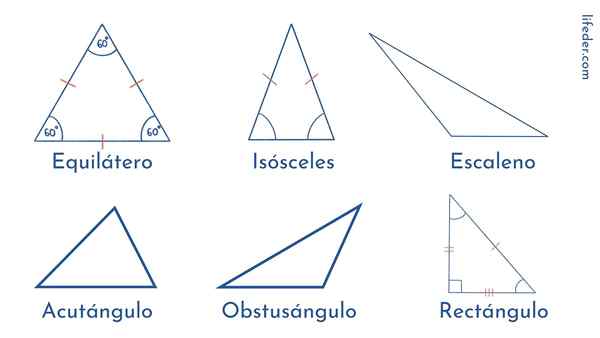
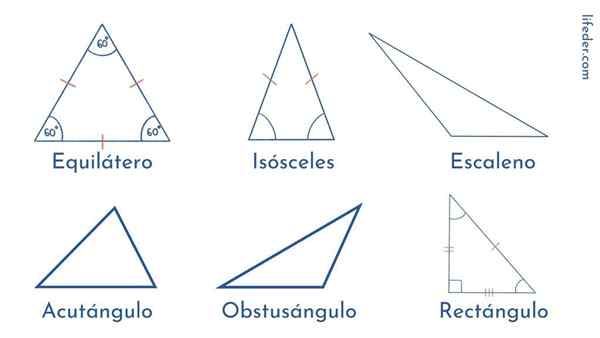
Segitiga diklasifikasikan mengikut panjang sisi mereka atau mengikut amplitud sudut mereka.

Jenis segitiga mengikut sisi mereka

Segitiga sama

Sisi segitiga jenis ini mempunyai panjang yang sama. Dan perkara yang sama berlaku untuk sudut mereka: Tiga ukuran 60º. Itulah sebabnya kita mengatakan bahawa segitiga sama rata adalah poligon biasa.

Segitiga Scalene

Tidak seperti sama, dalam segitiga scalene semuanya tidak sama: tiga sisinya mempunyai panjang yang berbeza dan sudutnya berbeza dalam amplitud.

Boleh melayani anda: Operasi gabungan

Segitiga Isosceles

Dalam segi tiga jenis ini kita dapati bahawa dua pihak mempunyai ukuran yang sama, sementara baki yang berbeza adalah berbeza. Yang sama diperhatikan dalam amplitud sudut: dua adalah sama dan satu berbeza.

Jenis segitiga mengikut sudut mereka

Segitiga kanan

Ia dicirikan dengan mempunyai sudut yang betul, iaitu, 90º. Dua sudutnya yang lain akut atau kurang daripada 90º.

Dalam segitiga jenis ini, bahagian terpanjang dipanggil hypotenusa, sementara dua pihak lagi adalah kategori.

Segitiga serong

Segitiga yang tidak mempunyai sudut yang betul milik jenis ini. Mereka dibahagikan kepada dua jenis:

Segitiga Acutangle: Tiga sudutnya teruk.

Segitiga bodoh: Mereka mempunyai dua sudut akut dan satu atau lebih besar daripada 90º.

Segitiga campuran

Segitiga yang sama dapat diklasifikasikan mengikut kedua -dua kriteria, iaitu, menurut panjang sisi mereka dan amplitud sudut mereka.

Sebagai contoh, segitiga segi empat tepat juga boleh menjadi eskalano atau isosceles, tetapi ia tidak boleh sama, kerana yang terakhir tidak hadir sudut yang betul.

Walau bagaimanapun, segitiga sama rata boleh menjadi akut, kerana ia berkesan mempunyai tiga sudut akut atau kurang daripada 90º.

Secara segitiga bodoh

Segitiga scalene boleh menjadi obtusely, kerana kedua -dua amplitud sudutnya dan panjang sisinya berbeza.

Cara mengira perimeter segitiga?

Produk jumlah panjang tiga sisi segitiga dipanggil perimeter.

Mari lihat beberapa contoh.

1- Kami diminta untuk mencari perimeter segitiga scalene yang sisi 6, 8 dan 4 sentimeter. Yang harus kita lakukan hanyalah menambah:

Dapat melayani anda: pemalar mutlak

6 + 8 + 4 = 18

Oleh itu, perimeter segitiga scalene ini adalah 10 sentimeter.

2- Kemudian mereka meminta kami untuk mengira perimeter segitiga isosceles yang sisinya mengukur 4 sentimeter dua dan 6 sentimeter yang tersisa. Oleh kerana dua sisinya mempunyai panjang yang sama, kita mesti meletakkan angka yang sama dua kali, seperti ini:

4 + 4 + 6 = 14

Perimeter segitiga ini adalah 14 sentimeter.

3- Contoh terakhir. Kami mempunyai tugas menentukan perimeter segitiga sama rata 9 sentimeter ke sisi. Seperti yang kita ketahui ciri -ciri pelbagai jenis segitiga, kita tahu bahawa sama rata dibezakan kerana tiga sisinya sama. Oleh itu:

9 + 9 + 9 = 27

Perimeter kesamaan ini ialah 27 sentimeter.

Meditrices, bisectors dan medium

Ini adalah tiga jenis garis lurus yang boleh ditarik dalam segitiga.

MediTrices

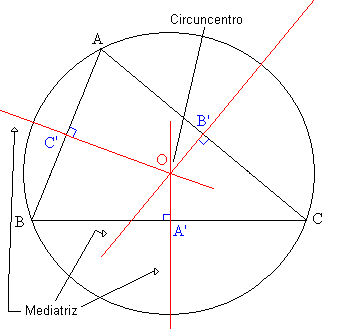
Terdapat tiga, satu di setiap sisi segitiga. Meditrix adalah garis lurus yang melewati titik tengah sisi segitiga yang mana ia sesuai. Tiga meditrices dari segitiga bersilang pada titik yang dikenali sebagai circumcentro, yang berada pada jarak yang sama dari setiap simpang segitiga.

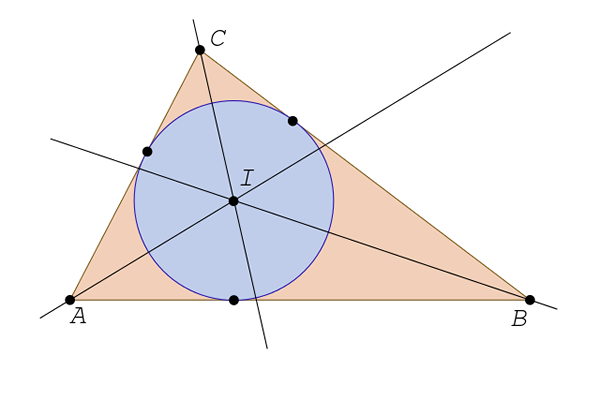
Bisectors

Terdapat tiga, satu untuk setiap sudut. Bisektor adalah garis lurus yang bermula dari puncak dan membahagikan sudut menjadi dua bahagian yang sama. Bisektor segitiga bersilang pada titik yang dikenali sebagai insenter.

Medium

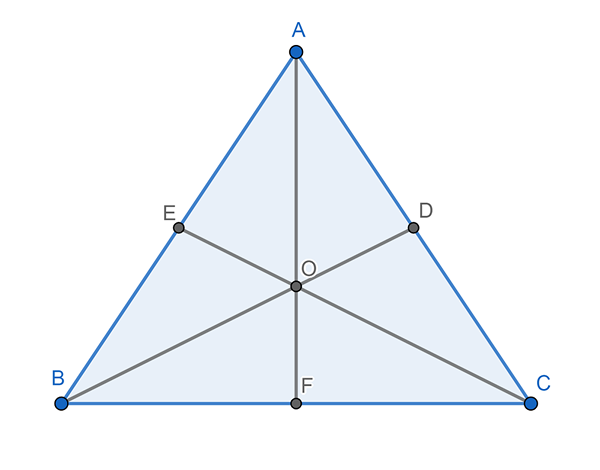
Terdapat juga tiga, satu untuk setiap puncak. Median adalah garis yang bermula dari puncak dan mencapai titik tengah di seberang. Median segitiga bersilang pada titik yang dipanggil baricentro.

Boleh melayani anda: ralat pensampelan: formula dan persamaan, pengiraan, contoh

Jarak antara mana -mana tiga simpang dan barycenter bersamaan dengan dua pertiga (2/3) dari jumlah panjang median yang sepadan. Sebagai contoh, jika median CE mengukur 5 sentimeter, maka jarak antara c dan balicenter (O) adalah sama 5 x 2/3, atau yang sama, 5 x 0.66, yang menghasilkan 3, 3 sentimeter.

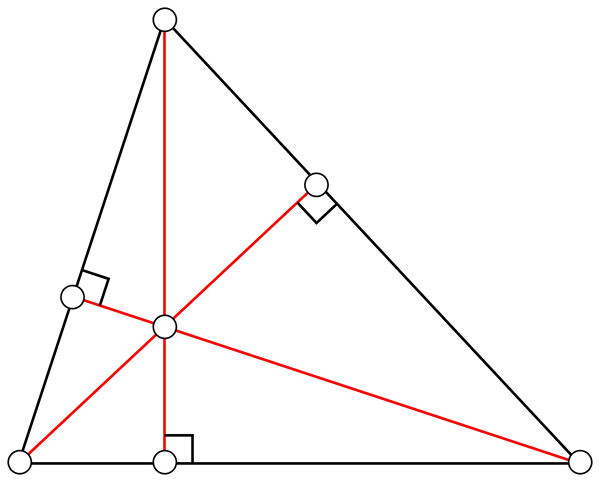
Ketinggian

Ia adalah garis lurus yang bergabung dengan puncak dengan sebaliknya. Tiga ketinggian segitiga bersilang pada titik yang dipanggil Ortotroenter. Bergantung pada jenis segitiga, orthocenter boleh berada di dalam atau di luar kawasan segitiga.

Cara Mengira Kawasan Segitiga?

Kawasan segitiga dalam apa jua bentuk dapat diketahui ketika memohon formula berikut:

A = b x h / 2

Dalam persamaan ini, A merujuk kepada kawasan tersebut; b merujuk kepada pangkalan dan h adalah ketinggian.

Mari lihat contoh. Kami diminta untuk mengira kawasan segitiga yang asasnya mengukur 12 sentimeter dan ketinggiannya adalah 7 sentimeter. Oleh itu, kita ada:

B = 12

H = 7

Kami menggunakan formula:

A = 12 x 7/2

A = 84/2

A = 44

Oleh itu, segitiga ini mempunyai kawasan seluas 44 sentimeter persegi.