Ciri trajektori fizikal, jenis, contoh dan latihan

The Trajektori dalam Fizik Ia adalah lengkung yang menggambarkan mudah alih ketika melewati titik berturut -turut semasa pergerakannya. Oleh kerana ini dapat mengamalkan varian yang tidak terkira banyaknya, jadi mereka juga akan menjadi trajektori yang dapat diikuti oleh mudah alih.

Untuk pergi dari satu tempat ke tempat lain, seseorang boleh mengambil jalan yang berbeza dan cara yang berbeza: berjalan kaki melalui trotoar di jalanan dan jalan, atau tiba dengan kereta atau motosikal di lebuh raya. Semasa perjalanan melalui hutan, walker boleh mengikuti trajektori rumit yang merangkumi giliran, memanjat atau menjatuhkan dan sehingga dia melewati beberapa kali melalui titik yang sama.

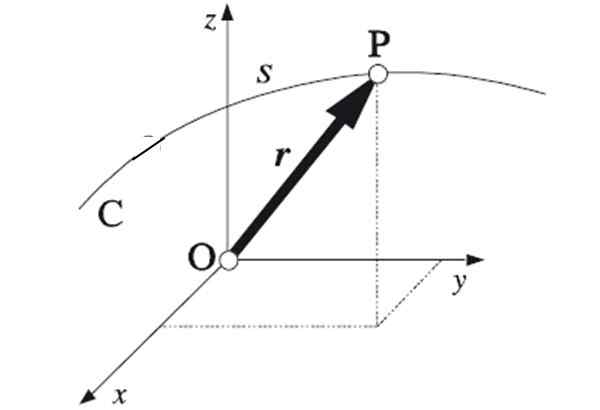Rajah 1. Menyertai titik melampau setiap vektor kedudukan trajektori diikuti oleh zarah diperolehi. Sumber: Algarabia [Domain Awam]

Sekiranya titik di mana bergerak bergerak mengikuti garis lurus, trajektori akan menjadi rectilinear. Ini adalah trajektori yang paling mudah, kerana menjadi satu -dimensi. Menentukan kedudukan memerlukan satu koordinat.

Tetapi telefon bimbit boleh mengikuti trajektori curvyl, dapat ditutup atau dibuka. Dalam kes ini, pemantauan kedudukan memerlukan dua atau tiga koordinat. Ini adalah pergerakan dalam satah dan ruang masing -masing. Ini ada kaitan dengan pautan: Mengehadkan keadaan material pergerakan. Beberapa contoh adalah:

- Orbit yang menggambarkan planet -planet di sekeliling matahari ditutup trajektori berbentuk elips. Walaupun, dalam beberapa kes, mereka boleh menghampiri bulat, seperti dalam kes Bumi.

- Bola yang menendang gawang dalam tendangan gol mengikuti trajektori parabola.

- Burung dalam penerbangan menggambarkan trajektori curvilinear di ruang angkasa, kerana selain bergerak di atas kapal terbang, ia boleh naik atau tahap rendah pada kehendak.

Trajektori fizik boleh dinyatakan secara matematik apabila kedudukan mudah alih diketahui pada bila -bila masa. Menjadi r Vektor kedudukan, yang seterusnya mempunyai koordinat x, dan dan z Dalam kes paling umum pergerakan tiga dimensi. Mengetahui fungsi tersebut r (T) Trajektori akan ditentukan sepenuhnya.

[TOC]

Lelaki

Secara umum, trajektori boleh menjadi lengkung yang agak rumit, terutama jika anda ingin menyatakan secara matematik. Oleh itu, ia bermula dengan model yang paling mudah, di mana telefon bimbit bergerak pada garis lurus atau di atas kapal terbang, yang boleh menjadi lantai atau yang lain yang sesuai:

Pergerakan dalam satu, dua dan tiga dimensi

Trajektori yang paling banyak dikaji adalah:

- Rectilinear, Semasa melancong dengan garis mendatar, menegak atau cenderung. Bola dilemparkan secara menegak ke atas trajektori ini atau objek yang tergelincir menuruni bukit dengan pesawat cenderung juga. Mereka adalah satu pergerakan dimensi, koordinat tunggal sudah cukup untuk menentukan kedudukannya sepenuhnya.

- Parabola, di mana telefon bimbit menggambarkan arka parabola. Ia kerap, kerana objek yang dilancarkan secara serong di bawah tindakan graviti (peluru) mengikuti trajektori ini. Untuk menentukan kedudukan mudah alih, anda perlu memberi dua koordinat: x dan dan.

- Bulat, berlaku apabila zarah bergerak mengikuti lilitan. Ia juga biasa dan amalan harian. Banyak objek sehari -hari mengikuti trajektori bulat seperti tayar, kepingan jentera dan satelit di orbit, untuk memberikan beberapa contoh.

Boleh melayani anda: vektor melengkapkan: definisi, notasi, latihan

- Elips, Objek bergerak berikutan elips. Seperti yang dinyatakan pada mulanya, adalah trajektori bahawa planet -planet mengikuti di orbit di sekitar matahari.

- Hiperbolik, Objek astronomi di bawah tindakan daya pusat (graviti), boleh mengikuti trajektori elips (tertutup) atau hiperbolik (terbuka), ini kurang kerap daripada yang pertama.

- Heliks, o pergerakan lingkaran, seperti burung yang naik dalam arus terma.

- Sway atau pendulih, Telefon bimbit menggambarkan arka dalam pergerakan perjalanan bulat.

Contoh

Trajektori yang diterangkan di bahagian sebelumnya sangat berguna untuk cepat mendapatkan idea bagaimana pergerakan objek. Walau apa pun, perlu menjelaskan bahawa trajektori mudah alih bergantung pada lokasi pemerhati. Ini bermaksud bahawa peristiwa yang sama dapat dilihat dengan cara yang berbeza, mengikut mana setiap satu.

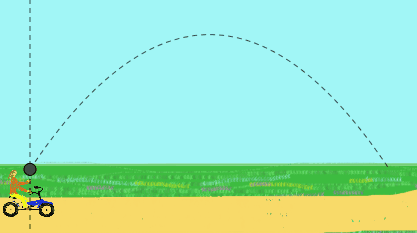
Contohnya pedal gadis pada kelajuan berterusan dan melemparkan bola. Dia memerhatikan bahawa bola menggambarkan trajektori rectilinear. 

Walau bagaimanapun, untuk pemerhati yang berdiri di jalan yang melihatnya, bola akan mempunyai pergerakan parabola. Baginya, bola pada mulanya dilemparkan dengan kelajuan yang cenderung, hasil kelajuan oleh tangan gadis itu ditambah dengan kelajuan basikal.

Rajah 2. Animasi ini menunjukkan pelancaran menegak bola yang dibuat oleh seorang gadis yang pergi dengan basikal, ketika dia melihat (trajektori rectilinear) dan ketika anda melihat pemerhati (trajektori parabola). (Disediakan oleh f. Zapata).

Trajektori mudah alih dengan cara yang jelas, tersirat dan parametrik

- Eksplisit, secara langsung menentukan lengkung atau tempat geometri yang diberikan oleh persamaan dan (x)

- Tersirat, di mana lengkung dinyatakan sebagai f (x, y, z) = 0

-Parametrik, Dengan cara ini koordinat x, dan y z berlaku bergantung pada parameter yang, secara umum, dipilih sebagai masa t. Dalam kes ini, trajektori terdiri daripada fungsi: x (t), dan (t) dan z (t).

Seterusnya, dua trajektori yang sangat dikaji terperinci dalam sinematik: trajektori parabola dan trajektori bulat.

Melancarkan dalam vakum

Objek (peluru) dilemparkan membentuk sudut A dengan mendatar dan dengan halaju awal v_{Sama ada} Seperti yang ditunjukkan oleh gambar. Rintangan udara tidak diambil kira. Pergerakan ini boleh dianggap sebagai dua pergerakan bebas dan serentak: satu mendatar dengan kelajuan menegak yang tetap dan lain di bawah tindakan graviti.

x (t) = x_{Sama ada} +v_lembu.t

dan (t) = y_{Sama ada} +v_Oy.T -½g.t²

Persamaan ini adalah Persamaan Parametrik pelancaran peluru. Seperti yang dijelaskan di atas, mereka mempunyai parameter biasa t, apa itu masa.

Di segitiga yang betul angka, berikut dapat dilihat:

v_lembu = v_{Sama ada} cos θ_Yo

v_Oy = v_{Sama ada} sin θ_Yo

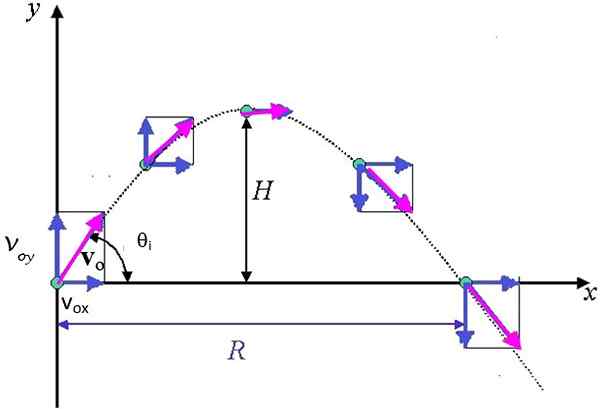Rajah 3. Trajektori parabola diikuti oleh peluru, yang menunjukkan komponen vektor kelajuan. H ialah ketinggian maksimum dan r adalah jangkauan mendatar maksimum. Sumber: Ayush12Gupta [CC BY-SA 4.0 (https: // creativeCommons.Org/lesen/by-sa/4.0)]

Dengan menggantikan persamaan ini yang mengandungi sudut pelancaran dalam persamaan parametrik itu:

Boleh melayani anda: Pembelahan bunyi: Apa, contoh, aplikasi

x (t) = x_{Sama ada} +v_{Sama ada} cos θ_Yo.t

dan (t) = y_{Sama ada} +v_{Sama ada}. sin θ_Yo.T -½g.t²

Persamaan trajektori parabola

Persamaan eksplisit trajektori adalah membersihkan t persamaan untuk x (t) dan menggantikan persamaan y (t) (t). Untuk memudahkan kerja algebra, dapat diandaikan bahawa asal (0.0) berada di titik pelancaran dan dengan cara ini x_{Sama ada} = y_{Sama ada} = 0.

Setelah memudahkan parameter "t"Ia telah dihapuskan dan persamaan yang kekal dan bergantung kepada x: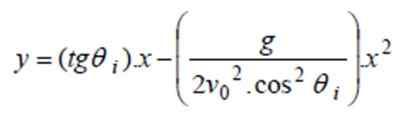

Ini adalah persamaan trajektori di Bentuk eksplisit.

Trajektori bulat

Trajektori bulat diberikan oleh:

(X - x_{Sama ada})² + (dan - dan_{Sama ada})² = R²

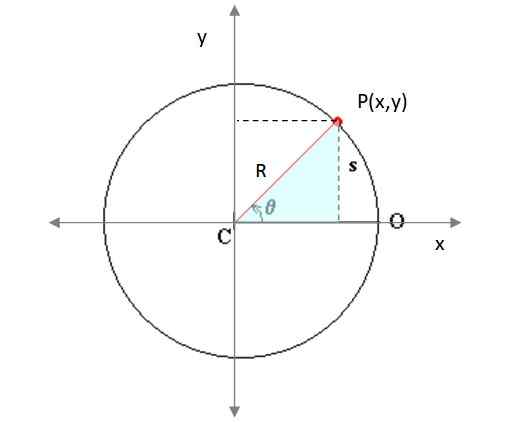Rajah 4. Zarah bergerak dalam trajektori bulat di atas kapal terbang. Sumber: diubahsuai oleh f. Wikimedia Commons Shoe.

Di sini x_{Sama ada} dan dan_{Sama ada} Mereka mewakili pusat lilitan yang diterangkan oleh mudah alih dan r adalah jejari yang sama. P (x, y) adalah titik trajektori. Dari segi empat tepat segi empat tepat (Rajah 3) ia diberi amaran bahawa:

x = r. cos θ

y = r. sin θ

Parameter, dalam kes ini, adalah sudut sapuan θ, yang dipanggil anjakan sudut. Dalam kes tertentu bahawa halaju sudut Ω (sudut menyapu per unit masa) adalah malar, ia dapat ditegaskan bahawa:

θ = θ_{Sama ada} + Ωt

Di mana θ_{Sama ada} Ia adalah kedudukan sudut awal zarah, yang jika diambil sebagai 0, dikurangkan ke:

θ = Ωt

Dalam kes ini, masa kembali ke persamaan parametrik seperti:

x = r.cos Ωt

y = r. dosa Ωt

Vektor unit Yo dan J Mereka sangat mudah untuk menulis fungsi kedudukan objek r (T). Mereka menunjukkan arahan pada paksi x dan pada paksi dan masing -masing. Dalam istilahnya, kedudukan zarah yang menggambarkan pergerakan pekeliling seragam adalah:

r (t) = r.cos Ωt Yo + R. dosa Ωt J

Latihan yang diselesaikan

Latihan diselesaikan 1

Meriam boleh menembak peluru dengan kelajuan 200 m/s dan sudut 40º berkenaan dengan mendatar. Sekiranya pelancaran dijalankan di kawasan rata dan rintangan udara dihina, cari:

a) persamaan trajektori dan (x) ..

b) Persamaan parametrik x (t) dan dan (t).

c) jangkauan mendatar dan masa peluru berlangsung di udara.

d) Ketinggian di mana peluru terletak ketika x = 12.000 m

Penyelesaian untuk)

a) Untuk mencari trajektori, nilai yang diberikan dalam persamaan y (x) bahagian sebelumnya diganti:

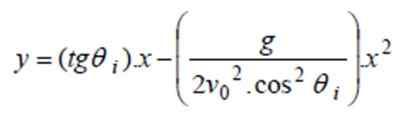
dan (x) = Tg 40º. x - 9.8/(2 '400². cos²40º) x² ⇒  dan (x) = 0.8391 x - 0.0000522X²

Penyelesaian b)

b) Titik pelancaran dipilih pada asal sistem koordinat (0.0):

x (t) = x_{Sama ada} +v_lembu.T = 400'Cos 40º.T = 306.42. t.

dan (t) = y_{Sama ada} +v_Oy.T -½g.t²= 400 'Sen 40º.T - 0.5 '9.8't²= 257.12 T - 4.9.t²

Penyelesaian c)

c) Untuk mencari masa bahawa peluru berlangsung di udara, ia selesai dan (t) = 0, Menjadi pelancaran dibuat di kawasan rata:

Boleh melayani anda: apa kekasaran relatif dan mutlak?

0 = 257.12.T - 4.9.t²

T = 257.12/4.9 s = 52.473 s

Skop maksimum mendatar menggantikan nilai ini dalam x (t):

x_Maks = 306.42'52.47 m = 16077.7 m

Cara lain untuk mencari x_Maks Ia secara langsung melakukan y = 0 dalam persamaan trajektori:

0 = 0.8391 x_Maks - 0.0000522 x²_Maks

x = 0.8391/0.0000522 m = 16078.5m

Terdapat perbezaan kecil kerana pembulatan perpuluhan.

D) penyelesaian

d) Untuk mengetahui ketinggian apabila x = 12000 m Nilai ini diganti secara langsung dalam persamaan trajektori:

dan (12000) = 0.8391'12000 - 0.0000522'12000² M = 2552.4 m

Latihan diselesaikan 2

Fungsi kedudukan objek diberikan oleh:

r (t) = 3t Yo + (4 -5t²) J m

Cari:

a) Persamaan untuk trajektori. Lengkung apa?

b) Kedudukan awal dan kedudukan apabila t = 2 s.

c) anjakan yang dibuat selepas t = 2 s.

Penyelesaian

a) Fungsi kedudukan telah diberikan dari segi vektor unit Yo dan J, yang masing -masing menentukan alamat pada paksi x dan dan, Oleh itu:

x (t) = 3t

dan (t) = 4 -5t²

Persamaan trajektori dan (x) Dia membersihkan t dari x (t) dan menggantikan dan (t):

T = x/3

dan (x) = 4 -5. (x/3)² = 4 - 5x²/9 (perumpamaan)

b) Kedudukan awal ialah: r (2) = 4 J m ; Kedudukan dalam T = 2 s adalah r (2) = 6 Yo -16 J m

c) anjakan Dr Ia adalah penolakan kedua -dua vektor kedudukan:

Δr = r (2) - r (2) = 6 Yo -16 J- 4 J = 6 Yo - dua puluh J m

Latihan diselesaikan 3

Bumi mempunyai jejari r = 6300 km dan diketahui bahawa tempoh putaran pergerakannya di sekitar paksi adalah satu hari. Cari:

a) Persamaan trajektori titik di permukaan bumi dan fungsi kedudukannya.

b) kelajuan dan percepatan titik tersebut.

Penyelesaian untuk)

a) Fungsi kedudukan untuk mana -mana titik dalam orbit bulat adalah:

r (t) = r.cos Ωt Yo + R.dosa Ωt J

Anda mempunyai jejari bumi r, tetapi bukan halaju sudut Ω, namun ia dapat dikira dari tempoh, mengetahui bahawa untuk pergerakan pekeliling itu sah untuk mengatakan bahawa:

Ω = 2π × Kekerapan = 2π / tempoh

Tempoh pergerakan adalah: 1 hari = 24 jam = 1440 minit = 86400 saat, oleh itu:

Ω =  2π / 86400 s = 0.000023148 ​​s^-1

Menggantikan fungsi kedudukan:

r (t) = r.cos Ωt Yo + R. dosa Ωt J = 6300 (kos 0.000023148T Yo + dosa 0.000023148T J) Km

Jalan dalam bentuk parametrik adalah:

x (t) = 6300. cos 0.000023148T

dan (t) = 6300. dosa 0.000023148T

Penyelesaian b)

b) Untuk pergerakan bulat, magnitud kelajuan linear v titik berkaitan dengan halaju sudut W melalui:

v = ΩR = 0.000023148 ​​s^-1'6300 km = 0.1458 km/s = 145.8 m/s

Walaupun menjadi pergerakan berterusan 145.8 m/s, Terdapat pecutan yang menunjuk ke pusat orbit bulat, yang bertanggungjawab untuk menjaga titik putaran. Ia adalah pecutan sentripetal ke_c, diberikan oleh:

ke_c = v² / R = (145.8 m/s)² / 6300 × 10³ m = 0.00337 m/s².

Rujukan

1. Giancoli, d. Fizik. (2006). Prinsip dengan aplikasi. 6^th Prentice Hall. 22-25.
2. Kirkpatrick, l. 2007. Fizik: Lihatlah dunia. 6^TA Edisi Singkat. Pembelajaran Cengage. 23 - 27.
3. Resnick, r. (1999). Fizikal. Jilid 1. Edisi ketiga dalam bahasa Sepanyol. Mexico. Syarikat Editorial Continental s.Ke. daripada c.V. 21-22.
4. Rex, a. (2011). Asas Fizik. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Fizik universiti dengan fizik moden. 14^th. Ed. Jilid1. 50 - 53.
6. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. 7^ma. Edisi. Mexico. Editor Pembelajaran Cengage. 23-25.
7. Serway, r., Vulle, c. (2011). Asas Fizik. 9^na Ed. Pembelajaran Cengage. 43 - 55.
8. Wilson, J. (2011). Fizik 10. Pendidikan Pearson. 133 - 149.