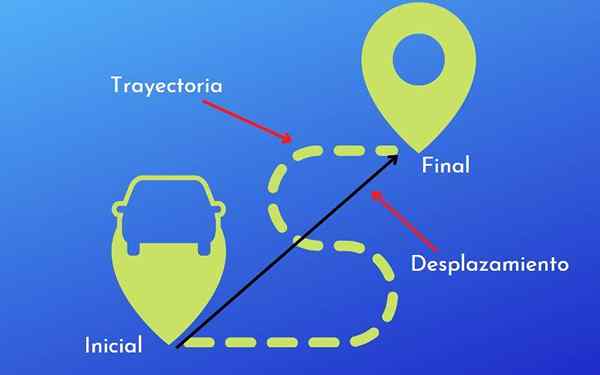
Trajektori dan anjakan

Perbezaan antara trajektori dan anjakan. Dengan lesen

The Perbezaan antara trajektori dan anjakan adalah bahawa yang terakhir adalah jarak dan arah yang dilalui oleh objek, sementara trajektori adalah laluan atau bentuk yang diterima pakai oleh pergerakan objek itu.

Walau bagaimanapun, untuk melihat lebih jelas perbezaan antara anjakan dan trajektori, lebih baik untuk menjelaskan melalui contoh -contoh yang membolehkan pemahaman yang lebih besar dari kedua -dua istilah.

Pemindahan

Difahamkan sebagai jarak dan arah yang dilalui oleh objek, dengan mengambil kira kedudukan awalnya dan kedudukan terakhirnya, selalu dalam garis lurus. Untuk pengiraannya, kerana ia adalah magnitud vektor, pengukuran panjang yang dikenali sebagai sentimeter, meter atau kilometer digunakan.

Formula untuk mengira anjakan ditakrifkan seperti berikut:

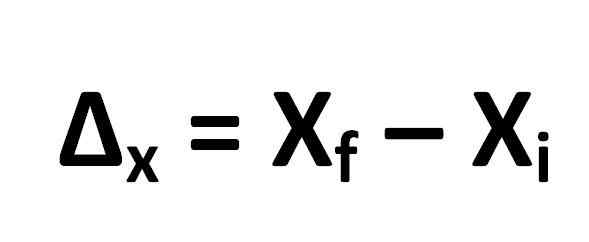
Dari mana ia mengikutinya:

- Δ_x = anjakan

- X_F = kedudukan akhir objek

- X_Yo = kedudukan objek awal

Contoh anjakan

1. Sekiranya sekumpulan kanak -kanak berada di permulaan laluan, kedudukan awalnya adalah 50 m, bergerak dalam garis lurus, menentukan anjakan di setiap titik x_F. 

- X_F = 120 m

- X_F = 90 m

- X_F = 60 m

- X_F = 40 m

2. Data masalah diekstrak dengan menggantikan nilai x₂ dan x₁ Dalam formula anjakan:

- Δ_x = ?

- X_Yo = 50 m

- Δ_x = X_F - X_Yo

- Δ_x = 120 m - 50 m = 70 m

3. Dalam pendekatan pertama ini kita mengatakan bahawa δ_x Ia sama dengan 120 m, yang sepadan dengan nilai pertama yang kita dapati dari x_F, kurang 50 m yang merupakan nilai x_Yo, Ia menghasilkan 70 m, iaitu, ketika mencapai 120 m mengembara anjakan adalah 70 m ke kanan.

Boleh melayani anda: cawangan makmal

4. Kami terus menyelesaikan dengan cara yang sama untuk nilai B, C dan D

- Δ_x = 90 m - 50 m = 40 m

- Δ_x = 60 m - 50 m = 10 m

- Δ_x = 40 m - 50 m = - 10 m

Dalam kes ini, anjakan memberi kita negatif, itu bermakna kedudukan akhir berada di arah yang bertentangan dengan kedudukan awal.

Trajektori

Ia adalah laluan atau garis yang ditentukan oleh objek semasa pergerakannya dan penilaiannya dalam sistem antarabangsa, ia secara umumnya mengamalkan bentuk geometri seperti garis, perumpamaan, bulatan atau elips.

Ia dikenal pasti melalui garis khayalan dan dengan kuantiti skalar ia diukur dalam meter.

Harus diingat bahawa untuk mengira trajektori yang mesti kita ketahui jika badan sedang berehat atau bergerak, iaitu, ia dikemukakan kepada sistem rujukan yang kita pilih.

Persamaan untuk mengira trajektori objek dalam sistem antarabangsa diberikan oleh:

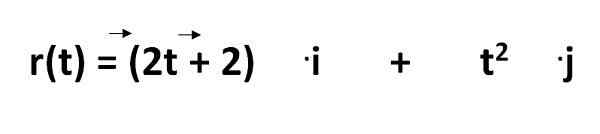
Yang mana kita harus:

- R (t) = ia adalah persamaan trajektori

- 2t - 2 dan t² = mewakili koordinat sebagai fungsi masa

-  ^.saya dan ^.J = Adakah vektor unit

Untuk memahami pengiraan trajektori yang dilalui oleh objek kita akan mengembangkan contoh berikut:

Kirakan persamaan trajektori vektor kedudukan berikut:

- R (t) = (2t + 7) ^.i + t^{2 .}J

- R (t) = (t - 2) ^.R & D 2T ^.J

Langkah pertama: Sebagai persamaan trajektori adalah fungsi x, untuk ini untuk menentukan nilai x dan y masing -masing dalam setiap vektor yang dibangkitkan:

1. Selesaikan vektor kedudukan pertama:

- R (t) = (2t + 7) ^.i + t^{2 .}J

2. Ty = f (x), di mana x diberikan oleh kandungan vektor unit ^.Saya dan diberikan oleh kandungan vektor unit ^.J:

Boleh melayani anda: ad hoc: asal istilah, makna dan contoh penggunaan

- X = 2t + 7

- Y = t²

3. y = f (x), iaitu, masa bukan sebahagian daripada ungkapan, oleh itu, kita mesti membersihkannya, kita ada:

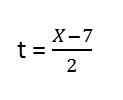
4. Kami menggantikan pelepasan dalam dan. Tinggal:

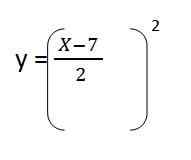
5. Kami menyelesaikan kandungan kurungan dan kami mempunyai persamaan trajektori yang dihasilkan untuk vektor unit pertama:

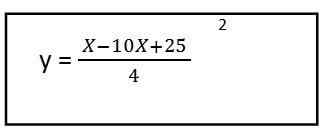
Seperti yang dapat kita lihat, ia menghasilkan persamaan darjah kedua, ini bermakna bahawa trajektori adalah untuk bentuk parabola.

Langkah kedua: Kami meneruskan dengan cara yang sama untuk pengiraan trajektori vektor unit kedua:

1. R (t) = (t - 2) ^.R & D 2T ^.J

- X = t - 2

- Y = 2t

2. Berikutan langkah -langkah yang kita lihat sebelum ini y = f (x), kita mesti membersihkan masa kerana ia bukan sebahagian daripada ungkapan, kita ada:

- t = x + 2

3. Kami menggantikan pelepasan dan tinggal:

- y = 2 (x + 2)

4. Menyelesaikan kurungan, kita mempunyai persamaan trajektori yang dihasilkan untuk vektor unit kedua:

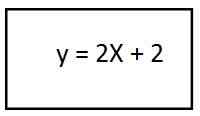
Dalam prosedur ini, kami menghasilkan garis, yang memberitahu kami bahawa trajektori mempunyai bentuk rectilinear.

Memahami konsep anjakan dan trajektori kita dapat menyimpulkan perbezaan yang lain di antara kedua -dua istilah.

Lebih banyak perbezaan antara anjakan dan trajektori

Pemindahan

- Ia adalah jarak dan arah yang dilalui oleh objek yang mengambil kira kedudukan awalnya dan kedudukan terakhirnya.

- Selalu berlaku dalam garis lurus.

- Diiktiraf dengan anak panah.

- Gunakan langkah panjang (sentimeter, meter, kilometer).

- Ia adalah jumlah vektor.

- Mengambil kira arah yang dilalui (kanan atau kiri)

- Tidak menganggap masa yang dihabiskan semasa lawatan.

Boleh melayani anda: pemeluwapan: konsep, proses, contoh

- Ia tidak bergantung pada sistem rujukan.

- Apabila titik permulaan adalah titik permulaan yang sama, anjakan adalah sifar.

- Modul mesti bertepatan dengan ruang untuk dilawati selagi trajektori adalah garis lurus dan tidak ada perubahan dalam erti kata untuk mengikuti.

- Modul ini cenderung meningkat atau berkurangan apabila pergerakan berlaku, dengan mengambil kira trajektori.

Trajektori

Ia adalah laluan atau garis yang ditentukan oleh objek semasa pergerakannya. Mengamalkan bentuk geometri (lurus, parabola, bulat atau elips).

- Ia diwakili melalui garis khayalan.

- Ia diukur dalam meter.

- Ia adalah kuantiti skalar.

- Tidak mengambil kira cara mengembara.

- Pertimbangkan masa yang dihabiskan semasa lawatan.

- Ia bergantung pada sistem rujukan.

- Apabila titik permulaan atau kedudukan awal adalah sama dengan kedudukan akhir, trajektori diberikan oleh jarak perjalanan.

- Nilai trajektori bertepatan dengan modul anjakan vektor, jika trajektori yang dihasilkan adalah garis lurus, tetapi tidak ada perubahan dalam pengertiannya.

- Ia selalu meningkat apabila badan bergerak, tanpa mengira trajektori.

Rujukan

1. Fernández, m., Fidalgo, j. (2016). Fizik dan Kimia Baccalaureate Pertama. Edisi Paraninfo, s.Ke. Sepanyol.
2. Institut Pendidikan Radio Guatemala (2011) Fizik Asas. Kumpulan Zaculeu Semester Pertama. Guatemala.