Tidecágono

Rajah 1.- Di sebelah kiri tridecácágone biasa dan di sebelah kanan mata wang 20 mahkota Republik Czech, dengan kontur berbentuk Bridecagon yang tertulis di lilitan, di satu pihak ia mempunyai singa bohemia dan di sisi lain ke San Wenceslao, penaung dari Republik Czech, dipasang pada menunggang kuda. Sumber: f. Zapata.

Apa itu tridecágono?

TrideCagon adalah tokoh geometri rata keluarga poligon dan yang dicirikan dengan mempunyai 13 sisi dan 13 simpul. Nama lain untuk poligon ini adalah Triskaidecágono, Bilangan yang diperoleh dari bahasa Yunani.

13 sisi adalah segmen garis yang akhirnya hampir membentuk angka. Poligon, yang dinamakan mengikut jumlah pihak, merupakan sumber inspirasi yang kaya untuk seni bina, pembinaan dan reka bentuk pelbagai objek, baik seni dan utilitarian.

Sifat Trideecágono

Saham Trideecágono dengan poligon lain ciri -ciri dan sifat berikut:

-Sisi, Mereka adalah segmen garis yang bergabung untuk membentuk angka, yang dalam kes tridecágono adalah 13. Mereka dikenal pasti dengan huruf kecil.

-Simpang, Inilah titik persimpangan sisi berturut -turut dipanggil dan biasanya menunjukkan huruf modal. Tridecágono mempunyai 13 simpang.

-Perimeter, bersamaan dengan jumlah sisi. Jika semua pihak mempunyai ukuran yang sama "A", perimeter hanya 13 × A, tetapi jika sisi tidak sama rata, maka perimeter menambahkan setiap panjang sisi.

-Pusat, Ia adalah titik yang mengekalkan jarak yang sama dengan kedua -dua simpang dan sisi.

-Pepenjuru, Barisan yang bergabung dengan puncak ke puncak yang tidak berturut -turut (simpang berturut -turut bersatu di sisi).

-Sudut dalaman, Mereka dibentuk di antara dua sisi bersebelahan angka dan di bahagian dalam poligon, dan puncaknya adalah puncak umum ke kedua -dua belah pihak.

Boleh melayani anda: miletus seperti teorem

-Sudut luaran, Mereka berada di luar poligon, di antara satu sisi dan pemanjangan salah satu sisi berturut -turut ke yang pertama.

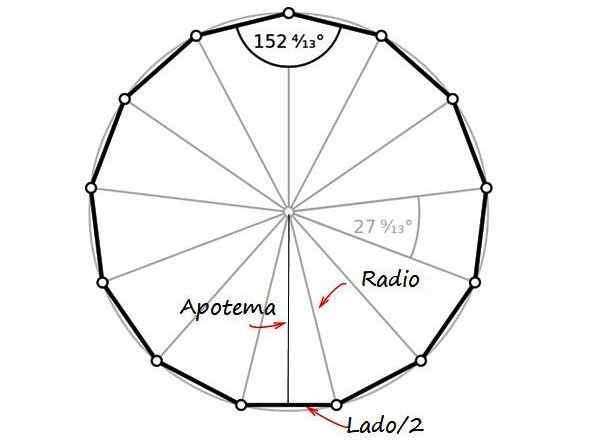
-Radio, Jarak jarak jauh dari tridecágon.

-Sudut pusat, Ia adalah yang puncaknya adalah pusat poligon.

-Apothem, segmen yang bergabung dengan pusat satu sisi dengan pusat angka dan bentuk 90º dengan sisi itu.

Guruh biasa dan tidak teratur

Threecarons boleh:

-Biasa, Apabila ukuran semua tiga belas sisi adalah sama dan sudut dalamannya mengukur sama.

-Tidak teratur, Sekiranya satu atau lebih sisi mempunyai langkah yang berbeza.

Dalam kes tridecácágone biasa, formula berikut boleh digunakan:

Sudut dalaman

Untuk poligon biasa, formula yang membolehkan untuk mengira nilai sudut dalaman adalah:

Di mana n mewakili bilangan pihak, yang dalam kes ini adalah 13. Dengan nilai ini:

I = (11 × 180º)/13 ≈ 152.Ke -3

Diagonal

Bilangan pepenjuru dikira oleh formula berikut, walaupun sah jika poligon tidak teratur:

Untuk n = 13 hasil:

D = 13 × 10/2 = 65 pepenjuru

Apothem

Nilai apothem l_Ke  Ia dikira dengan formula berikut, menjadi "A" panjang sisi:

L_Ke ≅ 2.0286A

Kawasan

Sekiranya perimeter p dan panjang apothem l_Ke, Kawasan Tridecágono dikira oleh:

A = (p × l_Ke)/2

Bergantung pada bahagian "A", formula kekal:

A = (13a × l_Ke)/2

Menggantikan ukuran_Ke Dari bahagian sebelumnya, formula untuk kawasan yang hanya bergantung pada panjang sisi diperolehi:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Boleh melayani anda: Pengedaran Hypergeometric: Formula, Persamaan, Model

Senaman

Sekiranya diameter mahkota 20 mm adalah 26 mm, berapa banyak sisi dan kawasan tridecágono yang didaftarkan dalam bulatan mata wang?

Penyelesaian

Dari angka terdapat segitiga segi empat tepat, kategori -kategori itu adalah apothem dan separuh panjang sisi, dengan hypotenusa sama dengan jejari mata wang, iaitu separuh dari diameter. Kerana ini bernilai 26 mm, Radio R adalah sama dengan 13 mm.

Rajah 2. Radio, apotheme dan separuh sisi trindecagon membentuk segitiga segi empat tepat. Sumber: Wikimedia Commons/F. Zapata.

Oleh Teorem Pythagoras:

Sejak l_Ke ≈ 2.0286a, anda ada:

R² = (2.0286a)² + (0.5)² = 4.3652a²

Sisi adalah:

Dengan nilai ini, kawasan mata wang adalah:

A ≈ 13.186a² = 13.186 (6.222mm)² = 510.5 mm²

Pembaca dibiarkan untuk membandingkan hasil ini dengan kawasan yang diperoleh dengan mengandaikan bahawa mata wang adalah bulat radius r = 13 mm.

Bagaimana tridecágono?

Trindecagon biasa adalah poligon yang tidak mengakui pembinaan yang tepat hanya menggunakan peraturan dan kompas, iaitu, ia bukan poligon yang boleh dibina. Mereka hanya boleh dibina, sekurang -kurangnya dalam teori, poligon yang jumlahnya hanya termasuk faktor utama bentuk:

Nombor utama seperti itu dipanggil Sepupu Fermat, Tetapi nombor 13, walaupun sepupu, tidak mempunyai borang ini.

Walau bagaimanapun, anda boleh melukis trindecagon biasa yang didaftarkan di lilitan, setiap puncak mempunyai persimpangan dengannya, tanpa diperhatikan di mata kasar. Untuk ini perlu.

Dapat melayani anda: segitiga obtusangle

Salah satu cara untuk membina tridecácágone biasa, walaupun bukan satu -satunya, menggambar strok seperti yang ditunjukkan dalam animasi berikut:

Rajah 3. Pembinaan tridecagon biasa. Sumber: Wikimedia Commons.

Dan animasi lain ini juga menerangkan cara membuat tridecágono kira -kira, dengan peraturan dan kompas:

Rajah 4.- Cara alternatif untuk membina tridecagon biasa dengan peraturan dan kompas. Sumber: Wikimedia Commons.

Contoh Trideecágel

Concave dan Convex Thunder

Apabila sudut dalaman tridecágono kurang dari 180º, angka itu adalah cembung, sementara jika satu atau lebih sudut dalaman lebih besar dari 180º, maka tridecágono adalah cekung.

Tridecácágon biasa adalah cembung, kerana sudut dalamannya mengukur kira -kira 152.Ketiga masing -masing.

Penggunaan tridecágono dalam numismatik

Mahkota Czech

Numismatics adalah sains duit syiling, pingat, tiket dan kerepek. Poligon di banyak pihak adalah ideal sebagai unsur hiasan dalam reka bentuk duit syiling, terutama yang mempunyai banyak sisi, seperti tridecágono.

Tidak semua duit syiling adalah bulat, bagaimanapun, poligon di banyak pihak menyerupai bentuk bulat, semakin banyak sisi yang ada, semakin besar pendekatan. Oleh itu, pereka duit syiling menggunakan poligon di banyak pihak untuk memperkenalkan sentuhan keaslian dalam reka bentuk mereka.

Pelbagai poligon digunakan dengan tujuan ini, seperti mata wang atas, yang dipanggil mahkota dan dari Republik Czech, contoh yang baik dari penggunaan tridecágono sebagai elemen reka bentuk.

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Lukisan. Poligon biasa. Pulih dari: melukis.com.
3. Hartley, m. Membina tridecagon. Pulih dari: youtube.com
4. Wikipedia. Poligon yang boleh dibina. Pulih dari: Adakah.Wikipedia.org.
5. Wikiwand. Tidecagon. Pulih dari: wikiwand.com.