Trinomial persegi sempurna

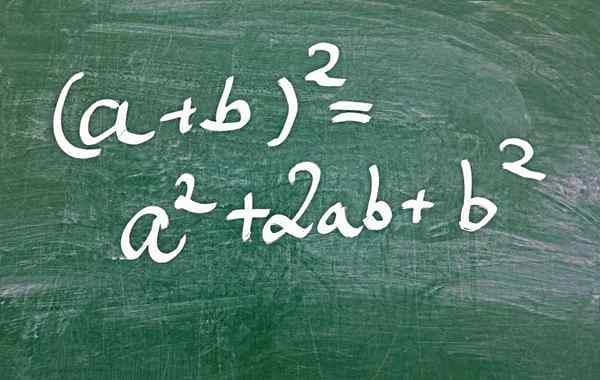Rajah 1.- Salah satu cara untuk mendapatkan trinomial persegi yang sempurna adalah melalui kuadrat jumlahnya

Apakah trinomial persegi yang sempurna?

Trinomial persegi yang sempurna adalah polinomial tiga istilah, dua daripadanya adalah dataran sempurna dari jumlah a dan b dan didahului oleh tanda yang sama, sementara istilah ketiga adalah tepat produk ganda a dan b, dapat menjadi tanda yang berbeza.

Trinomial persegi yang sempurna diperolehi dengan persegi jumlah atau perbezaan binomial dan algebra, bentuknya adalah seperti berikut:

ke² ± 2 ∙ ab + b²

Seperti yang dapat dilihat, trinomial persegi yang sempurna mengandungi:

• Dua istilah kuadratik yang tidak sama didahului dengan tanda yang sama: a² dan b²
• Istilah ketiga 2 ∙ ab, yang merupakan produk ganda akar persegi istilah kuadrat dan yang boleh didahului oleh tanda positif atau negatif.

Trinomial persegi yang sempurna boleh menjadi satu atau lebih pembolehubah. Sebagai contoh, trinomial berikut adalah persegi yang sempurna dari pembolehubah:

• x² + 6x + 9

Perhatikan bahawa terma pertama (x²) dan ketiga (9) adalah persegi, masing -masing, jumlah yang dipanggil A dan B. Sesungguhnya, x² Ia adalah persegi x dan 9 adalah persegi 3. Dengan cara ini anda boleh menulis perkara berikut:

a = x

B = 3

Dan istilah yang tinggal adalah produk berganda x dan 3:

6x = 2 ∙ 3 ​​∙ x

Sebaik sahaja pengesahan dibuat, pasti trinomial ini adalah persegi yang sempurna.

Contoh

Rajah 2.- Contoh trinomial persegi yang sempurna. Sumber: f. Zapata.

Trinomial persegi sempurna juga muncul dalam dua atau lebih pembolehubah, sebagai contoh:

4x² + 4xy + dan²

Ia adalah trinomial dalam dua pembolehubah: "x" dan "y". Ia dapat yakin bahawa ia adalah trinomial persegi yang sempurna, kerana ia membentangkan dua istilah kuadrat:

4x² = (2x)²

dan² = (y)²

Dan istilah yang tinggal adalah produk berganda dari akar persegi masing -masing: "2x" dan "y":

Boleh melayani anda: Orthoedro: formula, kawasan, kelantangan, pepenjuru, contoh

4xy = 2 ∙ 2x ∙ dan

Trinomial yang dibentangkan setakat ini adalah gred 2 dalam pembolehubah "x", tetapi mereka tidak semestinya harus seperti ini. Trinomial berikut adalah Gred 4 dalam "x":

9x⁴ - 30x²YZ + 25Y²z²

Mudah disahkan bahawa ini adalah trinomial persegi yang sempurna. Istilah pertama adalah persegi 3x yang sempurna², Sejak (3x²)² = 9x⁴.

Istilah 25y²z² sama dengan (5yz)². Akhirnya, istilah yang tinggal adalah 2 ∙ 3x²∙ 5yz = 30 x²dan z.

Sebaliknya, trinomial yang ditunjukkan di bawah tidak sempurna trinomial persegi:

• x²  + 8x - 16

Ia bukan trinomial persegi yang sempurna kerana 16, walaupun 4², Ia didahului oleh tanda negatif, sementara istilah kuadratik yang lain (x²) adalah positif.

• x²  - 15x + 25

Tidak juga trinomial persegi yang sempurna, kerana walaupun ia mempunyai dua istilah kuadratik: x² dan 5², Istilah 15x tidak sama dengan 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Trinomial ini tidak sempurna persegi, kerana ia hanya mengandungi istilah kuadratik: 4x² = (2x)².

Persegi jumlah dan persegi perbezaan

Trinomial persegi yang sempurna diperoleh dengan membangunkan dua jenis produk yang ketara:

• Dataran Jumlah.
• Dataran perbezaannya.

Pertama, pembangunan diperolehi dari harta pengedaran, sejak menaikkan tong binomial persegi mengalikannya dengan sendirinya:

(A ± b)² = (a ± b) × (a ± b) = a² ± a ∙ b ± b ∙ a + b² = a² ± 2a ∙ b + b²

Trinomial yang diperolehi adalah hasil yang dihafal dengan hanya sedikit amalan dan merupakan jalan pintas yang memudahkan pembangunan, itulah sebabnya ia dipanggil produk yang luar biasa.

Boleh melayani anda: nombor transenden: apakah, formula, contoh, latihan

Trinomial berikut mudah diperolehi oleh produk yang ketara, tanpa menggunakan harta pengedaran semula.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 dan² +20xy + 4x²

Pemfaktoran trinomial persegi yang sempurna

Operasi yang kerap dan perlu dalam algebra adalah pemfaktoran trinomial persegi yang sempurna, di mana trinomial dinyatakan sebagai kuadrat jumlah atau penolakan dua istilah (binomial).

Ia adalah operasi terbalik untuk membangunkan produk yang ketara, kerana mempunyai trinomial yang terhasil, idea itu adalah untuk mendapatkan binomial yang menimbulkannya apabila ia naik ke 2.

Contohnya, dalam trinomial persegi 4x sempurna yang dianalisis sebelumnya² + 4xy + dan², Apakah binomial yang apabila ia ditimbulkan, ia menimbulkan?

Akar persegi masing -masing istilah kuadrat adalah:

√ (4x²) = 2x

Yang bersamaan dengan: 4x² = (2x)²

√ (dan²) = y

Bersamaan dengan mengatakan bahawa: dan² = (y)²

Oleh itu:

4x² + 4xy + dan² = (2x + y)²

Dan apakah binomial yang berasal dari trinomial persegi sempurna 9x⁴ - 30x²YZ + 25Y²z²? Sekali lagi akar persegi istilah kuadrat diekstrak:

√ (9x⁴) = 3x²

√ (25 dan²z²) = 5yz

Jadi:

(3x² - 5yz)² = 9x⁴ - 30x²YZ + 25Y²z²

Latihan yang diselesaikan

Latihan 1

Dalam setiap trinomial berikut, lengkapkan kosong dengan istilah yang hilang menjadi trinomial persegi yang sempurna:

a) m² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Penyelesaian kepada

Menurut formula produk yang ketara:

Boleh melayani anda: sudut pelengkap: yang mana dan bagaimana ia dikira, contoh, latihan

(A ± b)² = A² ± 2a ∙ b + b²

Trinomial:

m² + 18m + _____

Ia mengikutinya:

a = m (jadi itu² = m²)

Di samping itu istilah pusat ialah: 2 ∙ A ∙ B = 2m ∙ b = 18m, oleh itu b = 9 dan perseginya adalah 9² = 81. Guy oleh formula produk yang terkenal, trinomial adalah seperti ini:

(M + 9)² = M² + 18m + 81

• Penyelesaian b

Dalam trinomial ini:

4x² - _____ + 64

Anda boleh tahu dan b:

A = √ (4x²) = 2x

B = √64 = 8

Oleh itu, istilah yang hilang adalah produk ganda A dan B:

2 ∙ AB = 2 ∙ 8 ∙ 2x = 32x

Dan trinomial yang dicari adalah:

4x² - 32x + 64

• Penyelesaian c

Di Trinomial:

_____ + 30n + 25

Istilah pertama hilang, tetapi diketahui bahawa:

B = √25 = 5

Dan

2 ∙ AB = 2 ∙ A ∙ 5 = 10A = 30N

Oleh itu A = 3n dan trinomial yang dicari adalah:

9n² + 30n + 25

Latihan 2

Semak bahawa seterusnya adalah trinomial persegi yang sempurna dan faktornya:

16y² - 24yz + 9z²

• Penyelesaian

Mula -mula terbukti bahawa istilah kuadratik didahului oleh tanda yang sama dan kemudian akar persegi masing -masing dijumpai:

A = √ (16y²) = 4y

B = √ (9z²) = 3z

Kemudian anda perlu mengesahkan sama ada istilah yang tinggal adalah produk ganda A dan B:

2 ∙ AB = 2 ∙ 4y ∙ 3z = 24yz

Sekiranya, maka trinomial boleh menjadi faktor sebagai persegi perbezaan, kerana istilah pusat didahului oleh tanda negatif:

16y² - 24yz + 9z² = (4y - 3z)²

Rujukan

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Pelajaran Matematik Kate. Trinomial persegi sempurna. Pulih dari: Katesmathesson.com.
3. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
4. Zill, d. 2008. Preccculment dengan kemajuan pengiraan. Ke -4. Edisi. McGraw Hill.