A Rhomboid Ia adalah tokoh rata empat sisi, -a segi empat tepat -di mana sisi dan sudut dalamannya berbeza dua hingga dua. Oleh itu rhomboid tergolong dalam kumpulan paralelogram serong.

Angka geometri adalah sebahagian daripada alam semula jadi dan khususnya empat pihak seperti rhomboid, mempunyai banyak aplikasi dalam seni bina dan reka bentuk.

Rajah 1. Panel pencahayaan Stadium Allianz Arena di Munich, Jerman, menerangi dengan warna pasukan tempatan dan dengan cahaya putih ketika pemilihan negara itu memainkan. Sumber: Pxhere.

Up kami mempunyai sebahagian daripada Fasad Stadium Bola Sepak Allianz Arena di Munich. Mereka adalah panel rhomboid yang menyala dengan warna pasukan tempatan.

Oleh itu, ia adalah angka dengan banyak dinamisme visual, kerana tidak seperti kuadrilatur lain, ia tidak mempunyai paksi simetri. Angka berikut menunjukkan pelbagai rhomboid dengan orientasi yang bervariasi dalam satah.

Rajah 2. Beberapa rhomboid dengan orientasi yang berbeza dalam pesawat. Sumber: f. Zapata.

[TOC]

Ciri -ciri romboid

Seterusnya, ciri -ciri utama angka geometri yang menarik ini:

-Nombor Lembaran: 4.

-Bilangan simpul: 4.

-Sisi yang bertentangan adalah sama dan selari, namun sisi bersebelahan tidak sama rata.

-Ia mempunyai 4 sudut dalaman: dua akut (kurang daripada 90º), dilambangkan oleh huruf Yunani α dan dua bodoh (lebih 180º), yang dipanggil β (lihat Rajah 3).

-Dengan menambahkan dua sudut bersebelahan rhomboid, 180º diperolehi, oleh itu α dan β adalah Tambahan.

-Jumlah sudut dalaman 4 adalah sama dengan 360º.

-Pepenjuru adalah segmen yang bermula dari puncak dan berakhir di puncak yang bertentangan.

-Titik di mana pepenjuru rhomboid bersilang dipanggil barycenter.

-Diagonal rhomboid mempunyai saiz yang berbeza.

Mengenai pepenjuru rhomboid Terdapat beberapa butiran penting yang akan kita bincangkan di bawah.

Boleh melayani anda: Menunggu garis: formula dan persamaan, perwakilan, contoh

Pepenjuru rhomboid

Sangat penting untuk menekankan bahawa pepenjuru rhomboid tidak bisekrik, iaitu, mereka tidak membahagikan sudut dalaman angka itu menjadi dua bahagian yang sama.

Pepenjuru tidak berserenjang antara satu sama lain. Walau bagaimanapun, kita dapat dengan mudah mengira mereka dengan teorem kosinus. Oleh itu, pepenjuru utama d_M Dalam rhomboid Rajah 3 adalah:

D_M = √ (a² + b² - 2.Ab.cos β)

Dan pepenjuru kecil d_m Saya akan:

D_m = √ (a² + b² - 2.Ab.cos α)

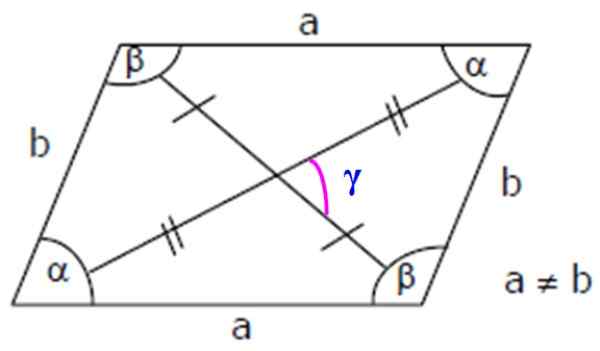Rajah 3. Unsur romboid: sisi, sudut dalaman dan pepenjuru. Sumber: Wikimedia Commons.

Penting: Sebagai α dan β adalah tambahan, ia dipenuhi bahawa:

dosa α = sin β

cos α = -cos β

Sifat -sifat sebab -sebab trigonometri ini mesti diambil kira semasa menyelesaikan latihan.

Cara mengeluarkan perimeter dan kawasan

Untuk mencari perimeter dan kawasan kami akan memberi nama kepada sisi rhomboid, ini akan menjadi ke dan b. Kami juga mempunyai ketinggian rhomboid, yang dipanggil h, yang merupakan garis yang diambil dari salah satu simpang dan diarahkan secara serentak ke seberang angka.

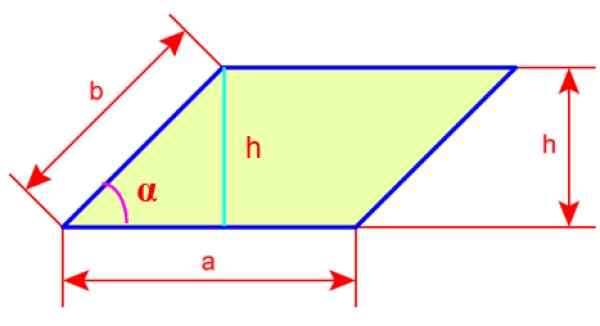Rajah 4. Ketinggian dan ketinggian rhomboid. Sumber: Wikimedia Commons.

Perimeter rhomboid

Perimeter rhomboid dikira dengan menambahkan panjang empat sisi. Mari panggil P ke perimeter, maka:

P = 2a + 2b

Kita juga boleh menyatakannya melalui:

P = 2 (a+b)

Perimeter mengetahui ketinggian

Sekiranya kita kelihatan dengan baik, ketinggian h dapat ditentukan dari segitiga di sebelah kiri dalam Rajah 4. Side B akan menjadi hipotenus dan ketinggian H Cateto menentang sudut α, oleh itu:

sin α = bertentangan / hypotenusa cateto

Wahai:

sin α = h / b

Kemudian kita membersihkan B:

b = h / sin α

Kami menggantikan perimeter P:

P = 2 [a + (h / sin α)]

Kawasan Romboid

Kawasan rhomboid adalah ukuran permukaannya. Dan kerana ia adalah selaras, kawasannya diberikan oleh ungkapan yang terkenal:

Boleh melayani anda: Faktor umum untuk istilah pengelompokan: Contoh, Latihan

A = BASE X Ketinggian

Bahawa menurut Rajah 3 dan 4 ia dinyatakan melalui:

A = a x h

Kawasan mengetahui kedua -dua belah pihak dan sudut dalaman

Memohon trigonometri asas bahagian sebelumnya, kita dapati ungkapan yang setara untuk kawasan rhomboid:

H = b. dosa α

Maka kawasan itu seperti ini:

A = a. b. dosa α

Mengingat apa yang kita katakan di atas mengenai sudut tambahan, kita boleh menggantikan Sen α dengan sen β jika perlu.

Kawasan mengetahui pepenjuru dan sudut di antara mereka

Akhirnya, jika kita tahu pepenjuru d_M dan d_m, Plus sudut γ di antara mereka (lihat Rajah 3), kawasan ini boleh dikira oleh separuh produk pepenjuru melalui pangkuan sudut tersebut:

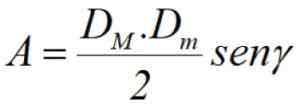
Latihan diselesaikan

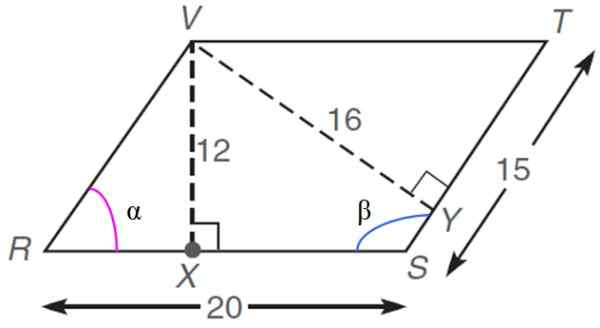
Dalam rhomboid berikut, dimensi yang diberikan dalam unit sewenang -wenangnya atau.ke., cari:

a) nilai perimeter

b) kawasan

c) sudut dalaman α dan β

d) Panjang segmen Rx

e) ukuran setiap pepenjuru

Penyelesaian kepada

Perimeter p ialah:

P = 2 (a + b)

Kami mengenal pasti terlebih dahulu nilai a dan b:

A = 20

B = 15

Kami menggantikan formula dan mengira:

P = 2. (20 + 15) = 70 U.ke.

Penyelesaian b

Rajah memberikan ketinggian h = 12 u.A, oleh itu kawasan boleh dikira dengan formula:

A = a x h

A = 20 x 12 u.ke.² = 240 u.ke.²

Terlepas dari unit yang dipilih untuk mengukur sisi dan ketinggian, kawasan ini selalu dinyatakan dalam unit kuadrat.

Hasil yang sama jika anda mendapat ketika mengira kawasan dengan ketinggian lain rhomboid, yang bernilai 16 u.ke. Malah:

A = 16 x 15 u.ke.² = 240 u.ke.²

Penyelesaian c

Sudut α boleh dikira melalui:

Ia dapat melayani anda: langkah kedudukan, kecenderungan pusat dan penyebaran

H = b. dosa α

Oleh itu, nilai H dan B diketahui, oleh itu:

α = arcsen (h/b) = arcsen (12/15) = 53.Ke -13

Mengingat bahawa sudut α dan β adalah tambahan, ia dipenuhi:

α + β = 180º ⇒ β = 180 - 53.13th = 126.87º

Penyelesaian d

Panjang segmen Rx mudah dikira, kerana terdapat cukup maklumat untuk mencarinya. Contohnya melalui:

Rx = rv . cos α = 15 . Cos 53.Ke -13 u.ke. = 9 u.ke.

Juga melalui teorem pythagoras melalui segi empat tepat segi tiga sisi 15 dan 12 u.ke:

(RV)² = (Rx)² + h²

Mengosongkan panjang segmen faedah:

Rx = √ [(rv)² - h²] = √ [15² - 12²] = √81 = 9

Penyelesaian e

Ukuran salah satu pepenjuru, contohnya pepenjuru yang bergabung dengan vertices R dan T, yang merupakan pepenjuru utama, diberikan oleh teorem kosinus, seperti yang dijelaskan sebelumnya, jadi kita menggantikan nilai -nilai di sana:

D_M = √ (20² + 25² - 2. dua puluh. lima belas .Cos 126.87º) = 37.22 u.ke.

Untuk pepenjuru kecil:

D_m = √ (20² + 25² - 2. dua puluh. lima belas .Cos 53.13th) = 25.79 u.ke.

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Baldor, a. 1973. Geometri dan trigonometri. Editorial Kebudayaan Amerika Tengah.
3. Dan. Ke. 2003. Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universiti Medellin.
4. Jiménez, r. 2010. Matematik II. Geometri dan trigonometri. Edisi kedua. Prentice Hall.
5. Poligon biasa. Pulih dari: pasangan.kejuruteraan.USAC.Edu.Gt.
6. Formula Universe. Rhomboid. Pulih dari: universoformulas.com.
7. Wikipedia. Rhomboid. Pulih dari: Adakah.Wikipedia.org.