Kami menerangkan apa dan apakah langkah penyebaran, dan kami memberikan beberapa contoh

Apakah langkah penyebaran?

The Langkah -langkah penyebaran atau variasi, dalam statistik, mengukur berapa banyak pengagihan data dari nilai langkah pusat bergerak, seperti purata atau aritmetik purata. Nilainya sentiasa positif dan biasanya berbeza dari 0, kecuali dalam hal data yang sama.

Sekiranya ukuran penyebaran menghasilkan nilai yang kecil, ini bermakna data terletak sangat dekat dengan purata, tetapi jika ia besar, ini bermakna data lebih tersebar, oleh itu, jauh dari purata.

Langkah -langkah penyebaran sangat penting dari sudut pandang statistik, bukan sahaja sebagai petunjuk aritmetik variasi data, tetapi sebagai bantuan yang tidak ternilai apabila anda ingin meningkatkan kualiti, baik dalam pembuatan produk dan dalam penyediaan perkhidmatan.

Contoh ini adalah perhatian di bank. Masa purata melambatkan pelanggan apabila mereka membuat baris yang unik dan kemudian diedarkan di box office, adalah sama seperti jika mereka membuat garis individu di hadapan masing -masing.

Walau bagaimanapun, penyebaran lebih rendah dalam baris tunggal, yang bermaksud bahawa masa perhatian individu sangat serupa dengan setiap pelanggan. Pelanggan telah menyatakan bahawa mereka berasa lebih selesa dengan cara ini, walaupun masa penjagaan purata adalah sama dalam modaliti sama ada.

Langkah -langkah penyebaran utama

Yang utama adalah: pangkat, varians, sisihan piawai dan pekali variasi.

Julat

Peringkat R dari set data ditakrifkan kepada perbezaan antara nilai maksimum x_Maks dan nilai minimum x_min keseluruhan:

Rang = r = nilai maksimum - nilai minimum = x_Maks - x_min

Boleh melayani anda: Apakah nombornya? 8 kegunaan utama

Julatnya cepat dikira, tetapi sangat sensitif terhadap nilai -nilai yang melampau, dan mempunyai kelemahan yang tidak mengambil kira nilai perantaraan. Oleh itu, ia hanya digunakan untuk mempunyai idea awal, cukup anggaran mengenai penyebaran data.

Contoh pangkat

Ini adalah senarai bilangan taufan di Atlantik dalam tempoh 14 tahun yang lalu:

8; 9; 7; 8; lima belas; 9; 6; 5; 8; 4; 12; 7; 8; 2

Data nilai maksimum ialah 15, dan nilai minimum ialah 2, oleh itu:

R = nilai maksimum - nilai minimum = x_Maks - x_min = 15 - 2 = 13 taufan

Varians

Ukuran ini digunakan untuk membandingkan setiap data dengan purata set, dan ia dikira dengan menambahkan perbezaan, tinggi persegi, antara setiap nilai dengan purata dan pembahagian dengan jumlah nilai.

Menjadi:

-Purata: μ

-Sebarang nilai, milik set data: x_Yo

-Jumlah pemerhatian: n

Menandakan varians penduduk seperti σ², Ungkapan untuk mengira ia adalah:

Dan apabila sampel populasi diambil, lebih suka mengira varians dengan cara ini:

Di mana varians sampel telah dilambangkan dengan s, dan purata sebagai x dengan bar, untuk meninggalkan penggunaan huruf Yunani kepada penduduk. Alasan untuk membahagikan antara n-1, bukannya n, adalah untuk varians sampel untuk tidak meremehkan penduduk, apa yang selalu berlaku apabila ia membahagikan antara n.

Sebaliknya, idea untuk mengukur setiap perbezaan antara data dan purata adalah untuk menghalang mereka daripada menambahkannya 0, kerana beberapa perbezaan akan positif dan negatif lain, yang cenderung membatalkan jumlah. Sebaliknya, dataran sentiasa positif.

Ia boleh melayani anda: kebarangkalian kekerapan: konsep, bagaimana ia dikira dan contohnya

Oleh itu, varians sentiasa positif, walaupun perbezaan antara x_Yo Dan purata adalah negatif, dan kelebihan utama variansnya adalah bahawa ia mengambil kira setiap data set.

Tetapi ia mempunyai kesulitan bahawa unitnya tidak sama dengan data, contohnya, jika ini terdiri pada masa -masa, diukur dalam beberapa minit, varians set akan diberikan dalam beberapa minit ke dataran.

Contoh varians

Pengiraan varians memerlukan mencari purata. Mengambil data nombor taufan, purata dikira oleh:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 taufan.Oleh itu, varians adalah:

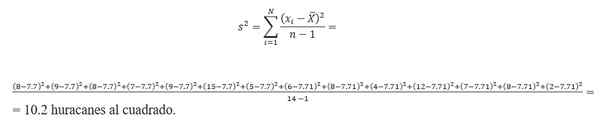
Sisihan piawai

Untuk membetulkan masalah kekurangan kesesuaian antara unit, sisihan piawai ditakrifkan σ, Seperti akar kuadrat varians:

Dan analogi, dalam hal sampel:

Terdapat peraturan empirikal untuk menganggarkan nilai sisihan piawai set data sampel, berdasarkan julat. Mengikut peraturan ini, sisihan piawai adalah kira -kira satu perempat daripada r:

S ≈ r/4

Ia mempunyai kelebihan yang membolehkan anggaran pesat sisihan piawai, kerana operasi lebih mudah.

Penyimpangan piawai adalah, dengan banyak, ukuran penyebaran yang paling biasa digunakan, jadi ia bernilai menonjolkan ciri -ciri utamanya:

• Penyimpangan piawai menunjukkan berapa banyak data media bergerak jauh
• Ia sentiasa positif, tetapi boleh menjadi 0 jika semua data adalah sama
• Semakin besar nilai sisihan piawai, semakin bertaburan adalah data
• Unit sisihan piawai adalah sama dengan pemboleh ubah yang sedang dikaji
• Nilainya berubah dengan cepat apabila salah satu data (atau lebih) mempunyai nilai yang sangat berbeza dari yang lain
• Nilai sisihan piawai adalah berat sebelah, iaitu, purata sisihan piawai tidak diedarkan sekitar purata, berbeza dengan varians, yang tidak diselaraskan.

Boleh melayani anda: acutangle triangle

Contoh sisihan piawai

Meneruskan dengan contoh taufan, sisihan piawai adalah:

Atau, jika lebih suka menggunakan pendekatan sisihan piawai melalui julat, nilai yang cukup dekat diperolehi:

S = 13/4 = 3.25

Pekali variasi

Koefisien variasi dilambangkan oleh inisial CV atau R, dalam beberapa teks, dan kedua -duanya untuk populasi, dan untuk sampel, mengaitkan sisihan piawai dan purata, sebagai peratusan:

Wahai:

Persamaan sah selagi purata berbeza dari 0.

Sebagai peraturan, pekali variasi dibulatkan kepada satu perpuluhan, dan digunakan untuk membandingkan data dari dua populasi yang berbeza.

Contoh pekali variasi

Waktu menunggu dalam beberapa saat, untuk pelanggan bank, direkodkan dalam dua situasi: ketika mereka membuat baris yang unik dan ketika mereka membuat pangkat individu sebelum pejabat tiket perhatian. Hasilnya adalah seperti berikut:

Kedua -dua set data boleh dibandingkan melalui pekali variasi masing -masing:

Baris tunggal

• Rata -rata = 429 saat
• Sisihan = 28.6 saat
• CV = (28.6/429) x 100 = 6.7 %

Pangkat individu

• Rata -rata = 429 saat
• Sisihan = 109.3 saat
• CV = (109.3/429) x 100 = 25.5 %

Oleh kerana nilai terakhir ini lebih besar, ini menunjukkan bahawa terdapat lebih banyak kebolehubahan dalam masa perkhidmatan pelanggan ketika mereka membuat pangkat individu daripada ketika mereka membuat baris unik, walaupun waktu rata -rata adalah sama dalam setiap kes.