Fizikal

Persamaan pengarah vektor garis, latihan yang diselesaikan

Persamaan pengarah vektor garis, latihan yang diselesaikan

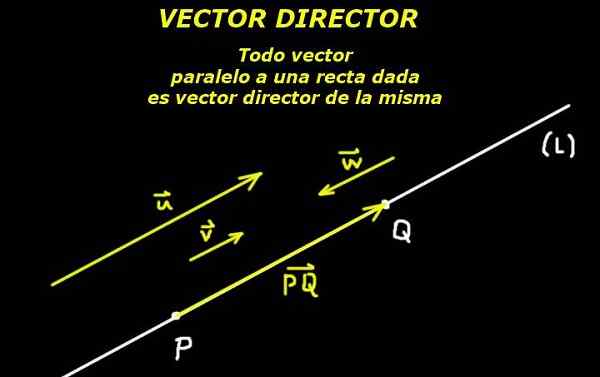
Ia difahami oleh Vektor Pengarah Orang yang mentakrifkan arah garis, sama ada dalam pesawat atau di angkasa. Oleh itu, vektor selari dengan garis boleh dianggap sebagai pengarah yang sama.

Ini mungkin terima kasih kepada aksiom geometri Euclidean yang mengatakan bahawa dua mata menentukan garis. Kemudian segmen berorientasikan yang membentuk kedua -dua mata ini juga mentakrifkan pengarah vektor garis itu.

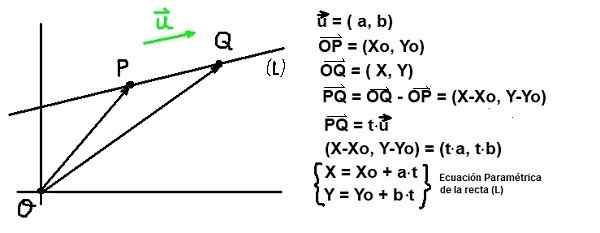
Rajah 1. Pengarah Vektor Talian. (Huraian sendiri)

Diberikan titik P kepunyaan garis (L) dan diberi vektor pengarah atau Garis itu, garis ditentukan sepenuhnya.

[TOC]

Persamaan garis dan pengarah pengarah

Rajah 2. Persamaan garis dan pengarah pengarah. (Huraian sendiri)

Diberikan titik P koordinat Q: (xo, saya) dan vektor atau Pengarah Talian (L), Semua titik Q koordinat Q: (x, y) mesti memenuhi bahawa vektor Pq selari dengan u. Keadaan terakhir ini dijamin jika Pq Ia berkadar dengan atau:

Pq = t ⋅atau

Dalam ungkapan sebelumnya t Ia adalah parameter yang dimiliki oleh nombor sebenar.

Sekiranya komponen Cartesian Pq dan dari atau Persamaan sebelumnya ditulis seperti berikut:

(X-xo, y-yo) = t (a, b)

Jika komponen kesamaan vektor adalah sama dengan sepasang persamaan berikut:

X - xo = a ⋅T      dan   Dan - saya = B ⋅T 

Persamaan parametrik garis

Koordinat X dan Dan satu titik milik garis (L) yang melalui titik koordinat (Xo, saya) Dan selari dengan Vektor Pengarah atau= (a, b) Mereka ditentukan dengan memberikan nilai sebenar kepada parameter pembolehubah t:

X = xo + a ⋅ t; Y = me + b ⋅T

Contoh 1

Untuk menggambarkan makna persamaan parametrik garis, kami ambil sebagai vektor pengarah

Boleh melayani anda: optik bergelora

atau = (a, b) = (2, -1) 

dan sebagai titik yang diketahui garis titik 

P = (xo, saya) = (1, 5). 

Persamaan parametrik garis adalah:

X = 1 + 2 ⋅T; Y = 5 - 1 ⋅T; -∞

Untuk menggambarkan makna persamaan ini Rajah 3 menunjukkan, di mana parameter t berubah nilai dan titik Q  koordinat (X, y) Ambil kedudukan yang berbeza di talian.

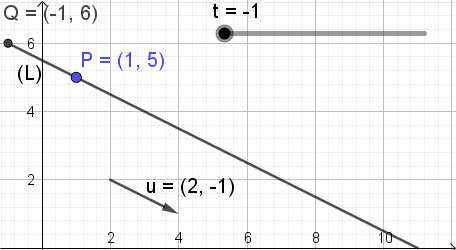Rajah 3. Pq = t u. (Huraian sendiri)

Garis dalam bentuk vektor

Memandangkan titik P garis dan pengarahnya atau persamaan garis boleh ditulis dalam bentuk vektor:

OQ = Op + λaraanatau 

Dalam persamaan sebelumnya yang mana -mana titik tetapi milik garis dan λ Nombor sebenar.

Persamaan vektor garisan boleh digunakan untuk sebilangan dimensi, bahkan hyper-eret dapat ditakrifkan.

Dalam kes tiga dimensi untuk vektor pengarah atau= (a, b, c) dan satu titik P = (xo, saya, zo), Koordinat titik generik Q = (x, y, z) Kepunyaan garis adalah:

(X dan z) = (Xo, i, zo) + λ ⋅ (a, b, c)

Contoh 2

Pertimbangkan lagi garis yang mempunyai sebagai pengarah pengarah  

atau = (a, b) = (2, -1) 

dan sebagai titik yang diketahui garis titik 

P = (xo, saya) = (1, 5). 

Persamaan vektor baris ini adalah:

(X, y) = (1, 5) + λaraan (2, -1) 

Bentuk garis berterusan dan vektor pengarah

Bermula dari bentuk parametrik, membersihkan dan memadankan parameter λ yang anda ada:

(X-xo)/a = (y-yo)/b = (z-zo)/c

Ini adalah bentuk simetri persamaan garis. Saya rasa itu ke, b dan c Mereka adalah komponen vektor pengarah.

Contoh 3

Pertimbangkan garis yang mempunyai sebagai pengarah pengarah  

atau = (a, b) = (2, -1) 

dan sebagai titik yang diketahui garis titik 

Boleh melayani anda: apakah elektriknya? (Dengan percubaan)

P = (xo, saya) = (1, 5). Cari bentuk simetri.

Bentuk simetri atau berterusan adalah garis adalah:

(X - 1)/2 = (y - 5)/( - 1)

Bentuk umum persamaan garis

Ia dikenali sebagai bentuk umum garis dalam satah XY kepada persamaan bahawa struktur berikut mempunyai:

A ⋅x + b ⋅Y = c

Ekspresi bentuk simetri boleh ditulis semula supaya ia mempunyai bentuk umum:

B ⋅x - a ⋅Y = b⋅xo - a ⋅o

Berbanding dengan bentuk umum garis kekal: 

A = b, b = -a dan C = B⋅xo - a ⋅O 

Contoh 3

Cari bentuk umum garis yang pengarahnya adalah u = (2, -1)

 Dan apa yang berlaku melalui titik p = (1, 5).

Untuk mencari bentuk umum kita boleh menggunakan formula yang diberikan, namun jalan alternatif akan dipilih.

Kami mulakan dengan mencari vektor dual vektor U, yang ditakrifkan sebagai vektor yang diperolehi dengan bertukar komponen U dan mendarab dengan -1 yang kedua:

W= (-1, -2)

Vektor dwi W sepadan dengan putaran dalam 90 ° dalam jadual pengarah pengarah v.

Kami melipatgandakan pendakian W dengan (X, y) Dan dengan (Xo, saya) Dan kita sepadan:

(-1, -2) • (x, y) = (-1, -2) • (1, 5)

-X -2y = -1 -2 ⋅5 = -11

Akhirnya tinggal:

X + 2y = 11

Bentuk standard persamaan garis

Ia dikenali sebagai bentuk standard garis dalam satah XY, yang mempunyai struktur berikut:

Y = m ⋅x + d

di mana m mewakili cerun dan d pemintasan dengan paksi dan.

Memandangkan pengarah u = (a, b) vektor, cerun m ialah b/a.

Dan D diperoleh dengan menggantikan x dan y oleh titik XO yang diketahui, saya:

I = (b/a) xo + d.

Pendek kata, m = b/a y d = saya -(b/a) xo

Perhatikan bahawa cerun m adalah kuota antara komponen dan pengarah dan komponen x yang sama.

Boleh melayani anda: keseimbangan putaran: formula dan persamaan, contoh, latihan

Contoh 4

Cari bentuk standard garis yang pengarahnya adalah u = (2, -1) 

Dan apa yang berlaku melalui titik p = (1, 5).

M = -½ dan d = 5 -( -½) 1 = 11/2

Y = (-1/2) x + 11/2

Latihan yang diselesaikan

-Latihan 1

Cari pengarah vektor garis (l) yang merupakan persimpangan satah (π): x - y + z = 3 dan satah (Ω): 2x + y = 1.

Kemudian tulis bentuk garis garisan yang berterusan (l).

Penyelesaian

Dari persamaan pesawat (Ω) pelepasan y: y = 1 -2x

Kemudian kita menggantikan persamaan satah (π):

X - (1 - 2x) + z = 3 ⇒ 3x + z = 4 ⇒ z = 4 - 3x

Kemudian kita parameterkan x, kita memilih parameterisasi x = λ

Ini bermakna garis mempunyai persamaan vektor yang diberikan oleh:

(X, y, z) = (λ, 1 - 2λ, 4 - 3λ)

yang boleh ditulis semula sebagai:

(X, y, z) = (0, 1, 4) + λ (1, -2, -3)

Dengan apa yang jelas bahawa vektor atau = (1, -2, -3) adalah vektor pengurusan lurus (L).

Bentuk garis berterusan (l) adalah:

(X - 0)/1 = (y - 1)/( - 2) = (z - 4)/( - 3)

-Latihan 2

Diberi pesawat 5x + ke Y + 4z = 5 

dan garis yang persamaannya adalah x/1 = (y-2)/3 = (z -2)/(-2)

Tentukan nilai ke Jadi satah dan garis selari.

Penyelesaian 2

Vektor n = (5, a, 4) adalah vektor biasa ke pesawat.

Vektor atau = (1, 3, -2) adalah pengurus lurus.

Sekiranya garis selari dengan pesawat, maka n • v = 0.

(5, ke, 4)•(1, 3, -2) = 5 +3ke -8 = 0 ⇒ ke= 1.

Rujukan

  1. Fleming, w., & Varberg, D. Dan. (1989). Matematik Prealculus. Prentice Hall Ptr.
  2. Kolman, b. (2006). Algebra linear. Pendidikan Pearson.
  3. Setia, j. M., & Viloria, n. G. (2005). Geometri analisis rata. Mérida - Venezuela: Editorial Venezuela C. Ke.
  4. Navarro, Rocio. Vektor. Pulih dari: buku.Google.co.Pergi.
  5. Pérez, c. D. (2006). Prequalculus. Pendidikan Pearson.
  6. Prenowitz, w. 2012. Konsep asas geometri. Rowman & Littlefield.
  7. Sullivan, m. (1997). Prequalculus. Pendidikan Pearson.