Pengiraan biasa dan contoh vektor

Dia Vektor biasa Ia adalah salah satu yang mentakrifkan arah tegak lurus ke entiti geometri yang dipertimbangkan, yang boleh untuk lengkung, satah atau permukaan, sebagai contoh.

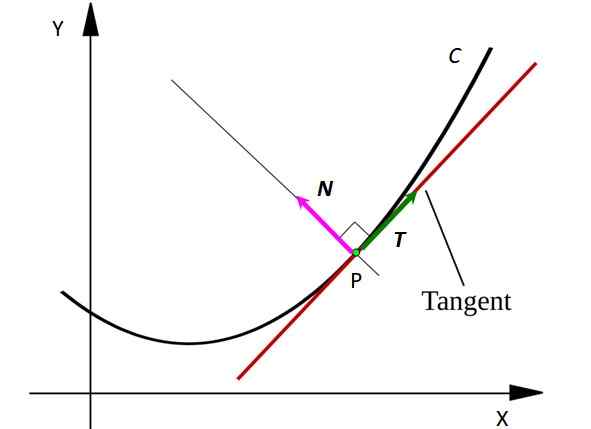
Ia adalah konsep yang sangat berguna dalam kedudukan zarah mudah alih atau permukaan di ruang angkasa. Dalam graf berikut, adalah mungkin untuk melihat bagaimana vektor biasa ke lengkung sewenang -wenangnya C:

Rajah 1. Lengkung c dengan vektor biasa ke lengkung pada titik p. Sumber: SVJO [CC BY-SA 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)]

Pertimbangkan titik p pada lengkung c. Titik boleh mewakili zarah mudah alih yang bergerak berikutan jalan berbentuk c. Garis tangen ke lengkung pada titik p kelihatan ditarik dengan warna merah.

Perhatikan bahawa vektor T Ia adalah tangen kepada c pada setiap titik, sementara vektor N berserenjang dengan T dan menunjuk ke pusat lilitan khayalan yang arka adalah segmen c. Vektor dilambangkan dalam huruf berani dalam teks bercetak, untuk membezakannya dari magnitud bukan vektor lain.

Vektor T Ia selalu menunjukkan di mana zarah bergerak, oleh itu ia menunjukkan kelajuan yang sama. Sebaliknya vektor N Sentiasa menunjuk ke arah di mana zarah beralih, dengan cara ini ia menunjukkan konkrit lengkung c.

[TOC]

Cara mendapatkan vektor biasa ke kapal terbang?

Vektor biasa tidak semestinya vektor unit, iaitu, vektor yang modulnya adalah 1, tetapi jika ya, ia dipanggil vektor unit biasa.

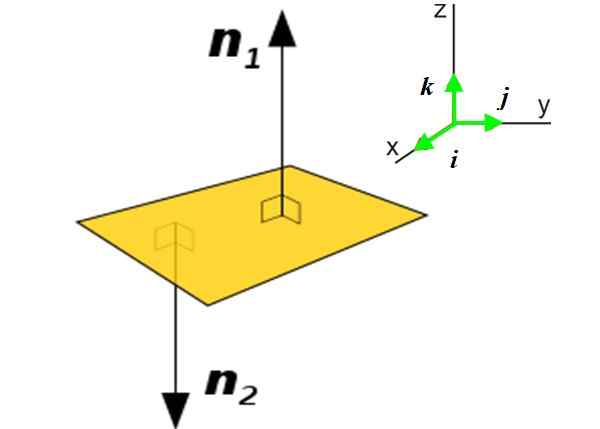
Rajah 2. Di sebelah kiri pesawat P dan dua vektor biasa untuk mengatakan pesawat. Di sebelah kanan vektor unit dalam tiga arah yang menentukan ruang. Sumber: Wikimedia Commons. Lihat halaman untuk pengarang [domain awam]

Dalam banyak aplikasi, perlu mengetahui vektor biasa ke satah dan bukannya lengkung. Vektor ini diketahui orientasi pesawat tersebut di ruang angkasa. Contohnya, pertimbangkan kapal terbang P (kuning) dari angka:

Ia dapat melayani anda: Gemine: Asal, Ciri -ciri dan Cara Memerhatikannya

Terdapat dua vektor biasa untuk pesawat itu: n₁ dan n₂. Penggunaan satu atau yang lain akan bergantung pada konteks di mana pesawat tersebut dijumpai. Mendapatkan vektor biasa ke satah sangat mudah jika persamaannya diketahui:

kapak + oleh + cz + d = 0, dengan ke, b, c dan d Nombor sebenar.

Nah, vektor pesawat biasa diberikan oleh:

N = a Yo + b J + c k

Di sini vektor N dinyatakan dari segi vektor unit dan tegak lurus antara satu sama lain Yo, J dan k, diarahkan ke seluruh tiga arah yang menentukan ruang X dan z, Lihat Rajah 2 Betul.

Vektor biasa dari produk vektor

Prosedur yang sangat mudah untuk mencari vektor biasa menggunakan sifat produk vektor antara dua vektor.

Seperti yang diketahui, tiga mata yang berbeza dan bukan colineal antara satu sama lain, tentukan pesawat P. Sekarang, ada kemungkinan untuk mendapatkan dua vektor atau dan v yang dimiliki oleh kapal terbang yang mempunyai tiga mata ini.

Setelah vektor, Produk vektor atau x v Ia adalah operasi yang hasilnya adalah vektor, yang mempunyai harta yang berserenjang dengan satah yang ditentukan oleh atau dan v.

Dikenali vektor ini, ia dilambangkan sebagai N, Dan daripadanya akan dapat menentukan persamaan pesawat terima kasih kepada persamaan yang ditunjukkan dalam bahagian sebelumnya:

N = atau x v

Angka berikut menggambarkan prosedur yang diterangkan:

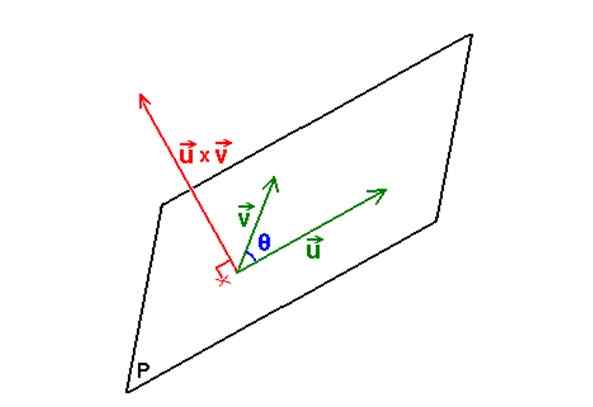Rajah 3. Dengan dua vektor dan produk vektor atau silang mereka, persamaan satah yang mengandungi kedua -dua vektor ditentukan. Sumber: Wikimedia Commons. Tiada pengarang yang boleh dibaca mesin yang disediakan. M.Romero Schmidtke diasumsikan (berdasarkan tuntutan hak cipta). [Domain awam]

Contoh

Cari persamaan satah yang ditentukan oleh titik A (2,1,3); B (0.1,1); C (4,2,1).

Boleh melayani anda: Persamaan kesinambungan

Penyelesaian

Latihan ini menggambarkan prosedur yang diterangkan di atas. Dengan mempunyai 3 mata, salah seorang daripada mereka dipilih sebagai asal usul bersama dua vektor yang tergolong dalam pesawat yang ditakrifkan oleh mata ini. Sebagai contoh, titik A ditetapkan sebagai asal dan vektor dibina Ab dan Ac.

Vektor Ab Ia adalah vektor yang asalnya titik A dan yang akhir adalah titik b. Koordinat vektor Ab Koordinat B koordinat A:

Ab = (0-2) Yo + (1-1) J + (1-3) k = -2Yo + 0J -2 k

Teruskan dengan cara yang sama untuk mencari vektor Ac:

Ac = (4-2) Yo + (2-1) J + (1-3) k = 2Yo + J -2 k

Pengiraan produk vektor Ab x ac

Terdapat beberapa prosedur untuk mencari produk vektor antara dua vektor. Dalam contoh ini, prosedur mnemonik digunakan yang menggunakan angka berikut untuk mencari produk vektor di kalangan vektor unit Yo, J dan K:

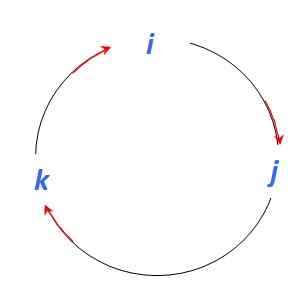Rajah 4. Grafik untuk menentukan produk vektor antara vektor unit. Sumber: Diri Diri.

Untuk memulakan adalah baik untuk diingat bahawa produk vektor antara vektor selari adalah tidak sah, oleh itu:

Yo x Yo = 0; J x J = 0; k x k = 0

Dan sebagai produk vektor adalah satu lagi vektor berserenjang dengan vektor yang mengambil bahagian, bergerak ke arah anak panah merah yang anda miliki:

Yo x J = k ; J x k = Yo; k x Yo = J

Sekiranya anda perlu bergerak bertentangan dengan anak panah maka tanda (-) ditambah:

J x Yo = - k; k x J = -Yo; Yo x k = -J

Secara keseluruhannya adalah mungkin untuk membuat 9 produk vektor dengan vektor unit Yo, J dan k, yang mana 3 akan menjadi tidak sah.

Ab x Ac = (-2Yo + 0J -2 k) X (2Yo + J -2 k) = -4 (Yo x Yo) -2 (Yo x J) +4 (Yo x k) +0 (J x Yo) + 0 (J x J) - 0 (J x k) - 4 (k x Yo) -2 (k x J) + 4 (k x k) = -2k-4J-4J+2Yo = 2Yo -8J-2k

Persamaan pesawat

Vektor N telah ditentukan oleh produk vektor yang dikira sebelum ini:

Boleh melayani anda: pergerakan pendulaan

N = 2Yo -8J-2k

Oleh itu a = 2, b = -8, c = -2, rancangan yang dicari adalah:

kapak + oleh + cz + d = 0 → 2x-8y-2z + d = 0

Nilai d. Ini mudah jika nilai mana -mana titik a, b atau c yang tersedia digantikan dalam persamaan pesawat. Memilih C sebagai contoh:

x = 4; y = 2; Z = 1

Ditinggalkan:

2.4 - 8.2 - 2.1 + d = 0

-10 + D = 0

D = 10

Pendek kata, pesawat yang dikehendaki adalah:

2x-8y-2z +10 = 0

Pembaca yang ingin tahu boleh bertanya sama ada hasil yang sama akan diperolehi jika bukannya melakukan Ab x Ac Ia akan dipilih Ac x Ab. Jawapannya adalah ya, pesawat yang ditentukan oleh ketiga -tiga titik ini adalah unik dan mempunyai dua vektor biasa, seperti yang ditunjukkan dalam Rajah 2.

Bagi titik yang dipilih sebagai asal vektor, tidak ada kesulitan dalam memilih mana -mana yang lain.

Rujukan

1. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. Diedit oleh Douglas Figueroa (USB). 31-62.
2. Mencari normal ke kapal terbang. Diperolehi dari: web.ma.Utexas.Edu.
3. Larson, r. (1986). Pengiraan dan geometri analisis. MC Graw Hill. 616 - 647.
4. Garis dan rancangan dalam r 3. Pulih dari: matematik.Harvard.Edu.
5. Vektor biasa. Pulih dari Mathworld.Wolfram.com.