Hasil pengiraan vektor, contoh, latihan

Dia Hasil vektor Ia adalah yang diperolehi oleh operasi dengan vektor yang hasilnya juga vektor. Biasanya operasi ini adalah jumlah dua atau lebih vektor, di mana vektor diperolehi yang bersamaan.

Dengan cara ini vektor seperti kelajuan, pecutan atau daya diperolehi yang dihasilkan. Contohnya apabila beberapa daya bertindak pada badan F₁, F₂, F₃,… . Jumlah vektor semua daya ini bersamaan dengan daya bersih (yang terhasil), yang secara matematik menyatakan dirinya:

F₁ + F₂ + F₃ +... = F_R  Sama ada F_N

Rajah 1. Berat salji diedarkan di atas siling dan tindakannya dapat digantikan oleh satu daya yang terhasil yang digunakan di tempat yang sesuai. Sumber: Pixabay.

Vektor yang dihasilkan, sama ada daya atau mana -mana magnitud vektor lain, memohon peraturan jumlah vektor. Oleh kerana vektor mempunyai arah dan rasa sebagai tambahan kepada nilai berangka, tidak cukup untuk menambah modul untuk mempunyai vektor yang dihasilkan.

Ini benar hanya dalam kes di mana vektor yang terlibat berada dalam arah yang sama (lihat contoh). Jika tidak, perlu menggunakan kaedah jumlah vektor, yang, bergantung pada kes itu, boleh menjadi geometri atau analisis.

[TOC]

Contoh

Kaedah Geometrik Untuk mencari vektor yang dihasilkan adalah kaedah poligon dan kaedah parallelogram.

Bagi kaedah analisis adalah kaedah komponen, di mana vektor yang dihasilkan dari mana -mana sistem vektor dapat dijumpai, selagi kita mempunyai komponen Cartesiannya.

Kaedah Geometrik Untuk Menambah Dua Vektor

Katakan vektor atau dan v (Kami menunjukkan mereka dengan berani untuk membezakannya dari skalar). Dalam Rajah 2) kita mempunyai mereka terletak di atas kapal terbang. Dalam Rajah 2 b) ia telah berpindah ke vektor v dengan cara yang asalnya bertepatan dengan akhir atau. Vektor yang dihasilkan dari asal usul yang pertama (atau) ke hujung yang terakhir (v):

Ia boleh melayani anda: kebolehmampatan: pepejal, cecair, gas, contoh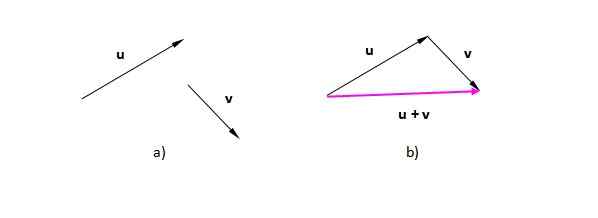 Rajah 2. Vektor yang dihasilkan dari jumlah vektor grafik. Sumber: Diri Diri.

Angka yang mengakibatkan kes ini adalah segitiga (segitiga adalah poligon 3 -sided). Sekiranya kita mempunyai dua vektor ke arah yang sama, prosedurnya adalah sama: letakkan salah satu vektor selepas yang lain dan lukiskan satu yang pergi dari asal atau ekor yang pertama ke hujung atau akhir yang terakhir.

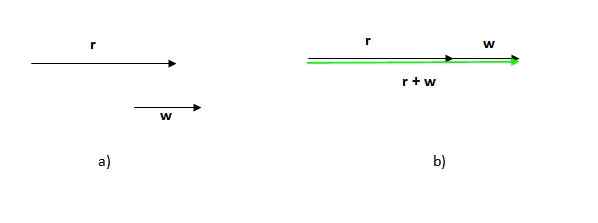
Perhatikan bahawa urutan di mana prosedur ini dibuat tidak penting, kerana jumlah vektor adalah komutatif.

Perhatikan juga bahawa dalam kes ini modul (Panjang atau saiz) vektor yang dihasilkan adalah jumlah modul vektor tambahan, tidak seperti kes sebelumnya, di mana modul vektor yang dihasilkan kurang daripada jumlah modul peserta.

Kaedah Parallelogram

Kaedah ini sangat sesuai apabila anda perlu menambah dua vektor yang titik asalnya setuju, dengan asal sistem koordinat x-y. Katakan ini adalah kes vektor kita atau dan v (Rajah 3):

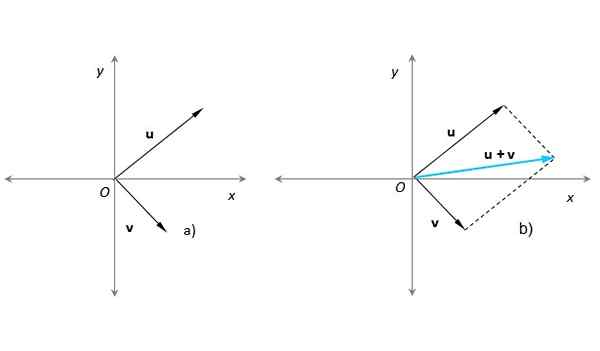Rajah 3. Jumlah dua vektor melalui kaedah paralelogram dengan vektor yang dihasilkan dalam biru biru. Sumber: Diri Diri.

Dalam Rajah 3b), sebuah selaras yang telah dibina dengan bantuan garis putus -putus selari ke atau sudah v. Vektor yang dihasilkan mempunyai asalnya di O dan akhir di titik di mana garis putus -putus bersilang. Prosedur ini sama dengan yang diterangkan di bahagian sebelumnya.

Latihan

-Latihan 1

Memandangkan vektor berikut, cari vektor yang dihasilkan menggunakan kaedah poligonal.

Ia dapat melayani anda: renungan cahaya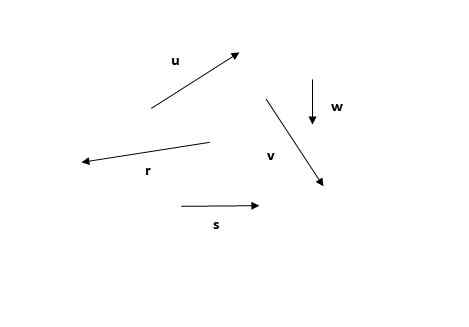 Rajah 4. Vektor untuk mencari hasilnya melalui kaedah poligon. Latihan 1. Sumber: Diri Diri.

Penyelesaian

Kaedah poligonal adalah yang pertama dari kaedah yang dilihat. Ingat bahawa jumlah vektor adalah komutatif (urutan penambahan tidak mengubah jumlahnya), jadi anda boleh bermula dengan mana -mana vektor, sebagai contoh atau (Rajah 5a) atau r (Rajah 5b):

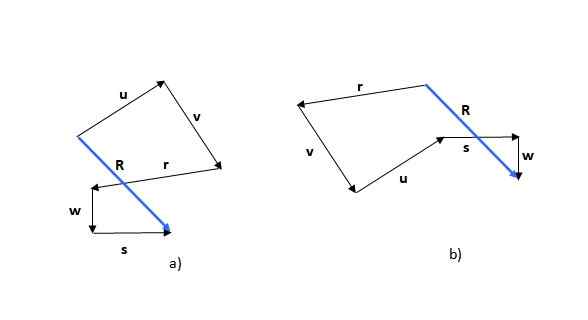Rajah 5. Jumlah vektor melalui kaedah poligonal. Sumber: Diri Diri.

Angka yang diperoleh adalah poligon dan vektor yang dihasilkan (berwarna biru) dipanggil R. Sekiranya anda bermula dengan vektor lain, angka yang terbentuk boleh berbeza, seperti yang dapat dilihat dalam contoh, tetapi vektor yang dihasilkan adalah sama.

Latihan 2

Dalam angka berikut diketahui bahawa modul vektor atau dan v masing -masing adalah u = 3 unit sewenang -wenangnya dan v = 1.8 unit sewenang -wenangnya. Sudut itu atau bentuk dengan paksi x positif adalah 45 º, sementara v Borang 60 º dengan paksi y, seperti yang dilihat dalam angka itu. Cari vektor, magnitud dan arah yang dihasilkan.

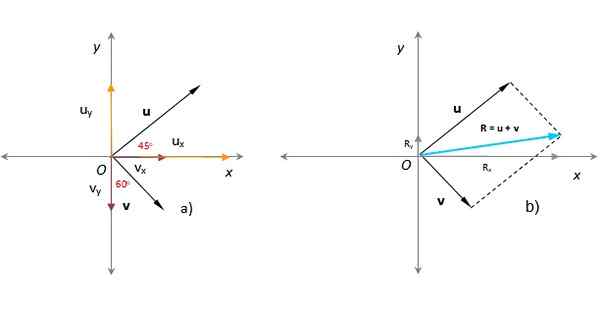
Penyelesaian

Di bahagian sebelumnya, vektor yang dihasilkan didapati menggunakan kaedah paralelogram (dalam turquoise dalam angka).

Cara mudah untuk mencari vektor yang dihasilkan secara analitik adalah untuk menyatakan vektor yang menambah dari segi komponen Cartesian mereka, yang merupakan tugas yang mudah apabila modul dan sudut diketahui, seperti vektor contoh ini:

atau_x = u . cos 45º = 3 x cos 45 º = 2.12; atau_dan = u . dosa 45 º = 3x sen 45º = 2.12

v_x = v . Sen 60º = 1.8 x sen 60 º = 1.56; v_dan = -V . cos 60 º = -1.8 x cos 60º = - 0.9

Boleh melayani anda: pergerakan pendulaan

Vektor atau dan v Mereka adalah vektor milik pesawat, mempunyai kedua -dua komponen masing -masing. Vektor U berada di kuadran pertama dan komponennya positif, manakala vektor V berada di kuadran keempat; Komponen xnya positif, tetapi unjurannya pada paksi menegak jatuh ke dalam paksi dan negatif.

Pengiraan komponen Cartesian vektor yang dihasilkan

Vektor yang dihasilkan menambah secara algebra komponen masing -masing x dan y, untuk mendapatkan komponen Cartesiannya:

R_x = 2.12 + 1.56 = 3.68

R_dan = 2.12 + (-0.9) = 1.22

Setelah komponen Cartesian telah ditentukan dan vektor diketahui sepenuhnya. Vektor yang dihasilkan boleh dinyatakan dengan notasi dalam kurungan persegi (kurungan):

R = Unit sewenang -wenangnya

Notasi kurungan digunakan untuk membezakan vektor dari satu titik dalam satah (atau di angkasa). Satu lagi cara untuk menyatakan vektor yang dihasilkan dengan cara analisis adalah melalui penggunaan vektor unit Yo dan j di atas kapal terbang (Yo, J dan k di ruang angkasa):

R = 3.68 Yo + 1.22 J Unit sewenang -wenangnya

Oleh kerana kedua -dua komponen vektor yang dihasilkan adalah positif, vektor R Ia tergolong dalam kuadran pertama, yang telah dilihat secara grafik.

Magnitud dan arah vektor yang dihasilkan

Dikenali dengan komponen Cartesian, magnitud r dikira melalui teorem Pythagoras, kerana vektor yang dihasilkan R, di sebelah komponennya r_x dan r_dan Mereka membentuk segitiga yang betul:

Magnitud atau modul: r = (3.68² + 1.22²)^½ = 3.88

Alamat q Mengambil paksi x positif sebagai rujukan: q = arcan (r_dan / R_x) = arctg (1.22/3.68) = 18.Ke -3

Rujukan

1. Menambah vektor dan peraturan. Pulih dari: newt.Phys.UNSW.Edu.Au
2. Figueroa, d. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik.31-68.
3. Fizikal. Modul 8: vektor. Pulih dari: frtl.Utn.Edu.ar
4. Hibbeler, R. 2006. Mekanik untuk jurutera. Statik. Edisi ke -6. Syarikat Editorial Continental. 15-53.
5. Vektor kalkulator tambahan. Pulih dari: www.1728.org