Sifat vektor percuma, contoh, latihan

The vektor percuma Mereka adalah yang ditentukan sepenuhnya oleh magnitud mereka, arah dan maknanya, tanpa perlu untuk menunjukkan titik permohonan atau asal tertentu.

Oleh kerana vektor tak terhingga dapat ditarik dengan cara ini, vektor percuma bukan entiti yang unik, tetapi satu set vektor selari dan identik yang bebas dari tempat di mana mereka berada.

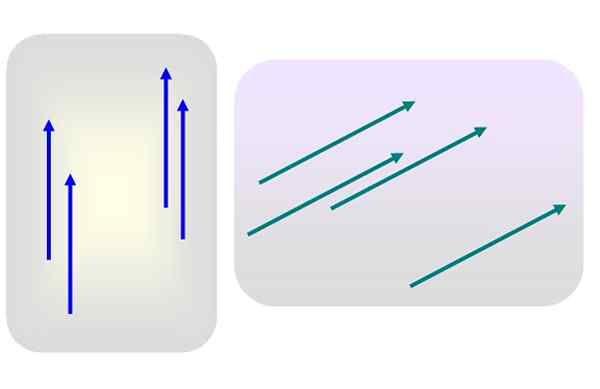
Rajah 1. Pelbagai vektor percuma. Sumber: Diri Diri.

Katakan terdapat beberapa vektor magnitud 3 yang diarahkan secara menegak, atau magnitud 5 dan cenderung ke kanan, seperti dalam Rajah 1.

Tiada vektor ini digunakan secara khusus untuk beberapa ketika. Kemudian mana -mana vektor biru atau hijau mewakili kumpulan masing -masing, kerana ciri -cirinya - modul, arah dan rasa - tidak diubah suai sama sekali apabila mereka dipindahkan ke tempat lain pesawat.

Vektor percuma biasanya dilambangkan dalam teks bercetak dengan huruf kecil dan berani, sebagai contoh v. Atau dengan huruf kecil dan anak panah di atas jika ia adalah teks manuskrip.

[TOC]

 Contoh

Kelebihan yang dimiliki oleh vektor bebas ialah mereka boleh dipindahkan dengan satah atau ruang dan mengekalkan sifat mereka, kerana mana -mana wakil set itu sama sah.

Itulah sebabnya dalam fizik dan mekanik sering digunakan. Sebagai contoh, untuk menunjukkan kelajuan linear pepejal yang bergerak tidak perlu memilih titik tertentu objek. Kemudian vektor kelajuan berkelakuan seperti vektor percuma.

Satu lagi contoh vektor percuma adalah pasangan daya. A pasangan Ia terdiri daripada dua daya magnitud dan arah yang sama, tetapi dari deria yang bertentangan, digunakan dalam titik yang berbeza dari pepejal. Kesan pasangan bukan untuk memindahkan objek, tetapi untuk menyebabkan putaran terima kasih kepada seketika dihasilkan.

Rajah 2 menunjukkan sepasang daya yang digunakan untuk stereng. Melalui kuasa F₁ dan F₂, Tork yang mengubah stereng di sekitar pusatnya dibuat dan dalam jadual.

Ia boleh melayani anda: boron nitride (bn): struktur, sifat, mendapatkan, menggunakan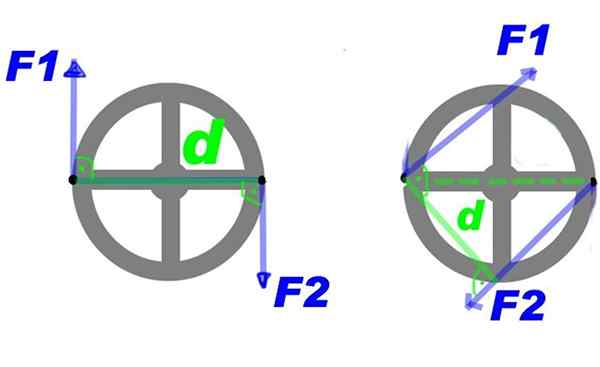 Rajah 2. Beberapa kuasa yang digunakan untuk stereng memberikan giliran pemarkahan. Sumber: Bensko [Domain Awam].

Anda boleh membuat beberapa perubahan pada pasangan dan terus memperoleh kesan berputar yang sama, contohnya meningkatkan daya, tetapi mengurangkan jarak di antara mereka. Atau mengekalkan kekuatan dan jarak, tetapi gunakan pasangan itu pada beberapa mata lagi pada stereng, iaitu, mengubah tork di sekitar pusat.

Masa pasangan kuasa atau sederhana pasangan, Ia adalah vektor yang modulnya FD dan berserenjang dengan satah roda tegak lurus. Dalam contoh yang ditunjukkan oleh konvensyen, giliran masa membuat akal negatif.

Sifat dan ciri -ciri

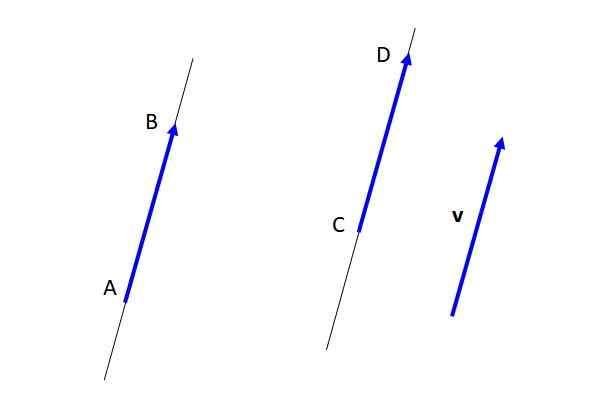
Tidak seperti vektor percuma V, vektor Ab dan CD Mereka tetap (lihat Rajah 3), kerana mereka telah menetapkan titik permulaan dan titik ketibaan. Tetapi menjadi peralatan antara satu sama lain, dan pada gilirannya dengan vektor v, Mereka mewakili vektor percuma v.

Rajah 3. Vektor percuma, peralatan dan vektor tetap. Sumber: Diri Diri.

Sifat utama vektor percuma adalah seperti berikut:

-Mana -mana vektor Ab (Lihat Rajah 2) Ia adalah, seperti yang dinyatakan, wakil vektor bebas v.

-Modul, arah dan makna adalah sama di mana -mana wakil vektor percuma. Dalam Rajah 2, vektor Ab dan CD Mereka mewakili vektor percuma v Dan mereka adalah peralatan.

-Memandangkan titik P ruang, selalu mungkin untuk mencari wakil vektor percuma v yang berasal dari p dan kata wakilnya adalah unik. Ini adalah harta yang paling penting dalam vektor bebas dan yang menjadikannya begitu serba boleh.

Boleh melayani anda: Eropah (satelit): ciri, komposisi, orbit, pergerakan

-Vektor percuma yang dilambangkan sebagai 0 Dan itu adalah set semua vektor yang kurang magnitud, arah dan makna.

-Jika vektor Ab mewakili vektor percuma v, Kemudian vektor Ba mewakili vektor percuma -v.

-Notasi akan digunakan V³ untuk menetapkan set semua ruang bebas ruang dan V² Untuk menetapkan semua vektor percuma pesawat.

Latihan yang diselesaikan

Dengan vektor percuma, anda boleh melakukan operasi berikut:

-Tambahan

-Penolakan

-Pendaraban pendakian oleh vektor

-Produk skalar antara dua vektor.

-Produk silang antara dua vektor

-Gabungan linear vektor

Dan banyak lagi.

-Latihan 1

Seorang pelajar berhasrat untuk berenang dari satu titik di pantai dari satu sungai ke sungai yang lain yang tepat di depan. Untuk mencapai apa -apa secara langsung pada kelajuan 6 km / j, dalam arah tegak lurus, namun arus mempunyai kelajuan 4 km / j yang mengalihkannya.

Kirakan kelajuan yang terhasil daripada perenang dan berapa banyak yang dialihkan oleh semasa.

Penyelesaian

Kelajuan perenang yang memanjangkan adalah jumlah vektor kelajuannya (berkenaan dengan sungai, ditarik secara menegak) dan kelajuan sungai (diambil dari kiri ke kanan), yang dijalankan seperti yang ditunjukkan dalam gambar di bawah:

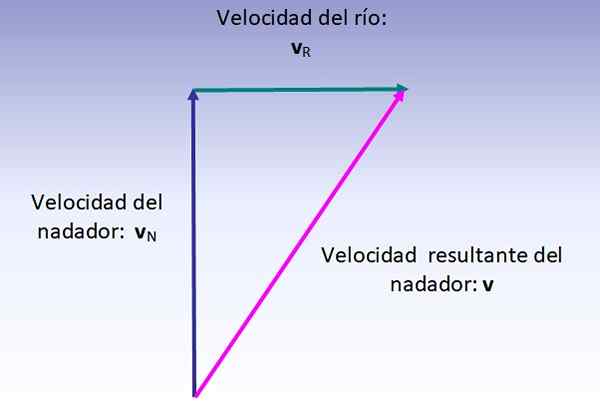
Besarnya kelajuan yang terhasil sepadan dengan hipotenus segitiga yang betul yang ditunjukkan, oleh itu:

V = (6² + 4²) ^½ km/h = 7.2 km/j

Alamat boleh dikira dengan sudut berkenaan dengan tegak lurus ke pantai:

α = arctg (4/6) = 33.7 atau 56.Ke -3 mengenai pantai.

Latihan 2

Cari masa pasangan kuasa yang ditunjukkan dalam gambar:

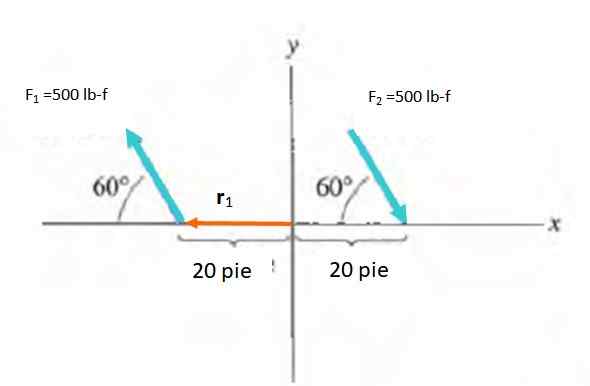
Penyelesaian

Masa ini dikira oleh:

Boleh melayani anda: kejutan tidak elastik: dalam dimensi dan contoh

M = r x F

Unit masa ini adalah lb-f.kaki. Oleh kerana tork berada dalam satah skrin, saat ini diarahkan tegak lurus kepadanya, sama ada ke luar atau ke dalam.

Oleh kerana tork contohnya cenderung untuk mengubah objek yang digunakan (yang tidak ditunjukkan dalam angka) dalam jadual, saat ini dipertimbangkan dengan menunjuk di dalam skrin dan dengan tanda negatif.

Besarnya momen adalah m = f.d.Dosa A, berada di sudut antara kekuatan dan vektor r. Anda mesti memilih titik untuk mengira masa ini, yang merupakan vektor percuma. Oleh itu, asal sistem rujukan dipilih r pergi dari o ke titik permohonan setiap daya.

M₁ = M₂ = -Fdsen60º = -500 . dua puluh .Sen 60º lb-f . kaki = -8660.3 lb-f . kaki

Momen bersih adalah jumlah m₁ dan m₂: -17329.5 lb-f . kaki.

Rujukan

1. Beardon, t. 2011. Pengenalan kepada vektor. Pulih dari: nrich.Matematik.org.
2. Bedford, 2000. Ke. Mekanik untuk Kejuruteraan: Statik. Addison Wesley. 38-52.
3. Figueroa, d. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik.31-68.
4. Fizikal. Modul 8: vektor. Pulih dari: frtl.Utn.Edu.ar
5. Hibbeler, R. 2006. Mekanik untuk jurutera. Statik. Edisi ke -6. Syarikat Editorial Continental. 15-53.
6. Vektor kalkulator tambahan. Pulih dari: 1728.org
7. Vektor. Pulih dari: ia adalah.Wikibooks.org