Pengiraan vektor pengimbang, contoh, latihan

Dia mengimbangi vektor Ia adalah yang membezakan vektor yang dihasilkan dan oleh itu ia dapat mengimbangi sistem, kerana ia mempunyai magnitud yang sama dan arah yang sama, tetapi bertentangan dengan ini.

Pada banyak kesempatan, vektor mengimbangi merujuk kepada vektor daya. Untuk mengira daya mengimbangi, daya yang dihasilkan adalah yang pertama, seperti yang ditunjukkan dalam angka berikut:

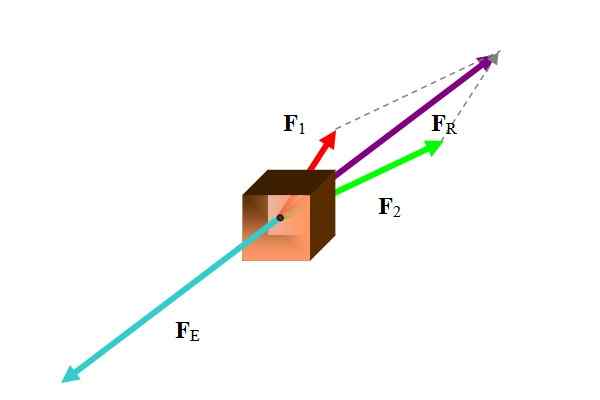
Rajah 1. Pada badan dua kuasa bertindak yang mengakibatkan seimbang dengan kekerasan dalam warna turquoise. Sumber: Diri Diri.

Terdapat pelbagai kaedah untuk melaksanakan tugas ini, mengikut data di tangan. Oleh kerana kekuatan adalah vektor, hasilnya adalah jumlah vektor kuasa yang mengambil bahagian:

F_R = F₁ + F₂ + F₃ +  … .

Antara kaedah yang akan digunakan adalah kaedah grafik seperti kaedah poligonal, paralelogram dan analisis seperti penguraian daya dalam komponen Cartesian mereka. Dalam contoh angka itu digunakan kaedah paralelogram.

Sebaik sahaja daya yang dihasilkan dijumpai, daya pengimbangan adalah tepat vektor yang bertentangan.

Yeah F_Dan Ia adalah kekuatan mengimbangi, maka ia dipenuhi F_Dan Digunakan pada satu ketika, ia menjamin keseimbangan terjemahan sistem. Jika ia adalah zarah tunggal, ia tidak akan bergerak (atau mungkin ia melakukannya dengan kelajuan yang berterusan), tetapi jika ia adalah objek yang dilanjutkan, ia masih akan mempunyai kemungkinan untuk beralih:

F_R + F_Dan = 0

[TOC]

Contoh

Daya pengimbangan hadir di semua sisi. Kita sendiri seimbang dengan kekuatan yang dikerahkan oleh kerusi untuk mengimbangi berat badan. Objek yang terdapat di rehat: buku, perabot, lampu siling dan sebilangan besar mekanisme, terus seimbang dengan daya.

Boleh melayani anda: kejutan tidak elastik: dalam dimensi dan contoh

Contohnya, buku rehat di atas meja seimbang dengan daya normal yang dikenakan ke atas buku itu, menghalangnya daripada jatuh. Begitu juga untuk rantai atau kabel yang memegang lampu yang tergantung dari siling di dalam bilik. Kabel yang memegang beban diedarkan berat badan mereka melalui ketegangan di dalamnya.

Dalam cecair beberapa objek dapat terapung dan kekal berehat, kerana beratnya seimbang dengan daya menaik yang dikenakan oleh cecair, yang dipanggil tolak.

Pelbagai mekanisme perlu seimbang mengetahui vektor daya mengimbangi seperti bar, rasuk dan lajur.

Apabila menggunakan keseimbangan, perlu entah bagaimana mengimbangi berat objek dengan daya yang bersamaan, sama ada menambah berat atau mata air.

Jadual Angkatan

Jadual Angkatan digunakan di makmal untuk menentukan daya seimbang. Ia terdiri daripada platform bulat, di mana anda mempunyai pandangan atas dalam angka itu, dan itu mempunyai pengangkut untuk mengukur sudut.

Di tepi meja terdapat kendi di mana rentetan yang memegang berat dan berkumpul di gelung yang ada di tengah.

Contohnya dua berat digantung. Ketegangan yang dihasilkan pada rentetan oleh berat ini ditarik merah dan biru dalam Rajah 2. Ketiga beratnya hijau, dapat mengimbangkan kekuatan yang terhasil dari dua yang lain dan menjaga keseimbangan sistem.

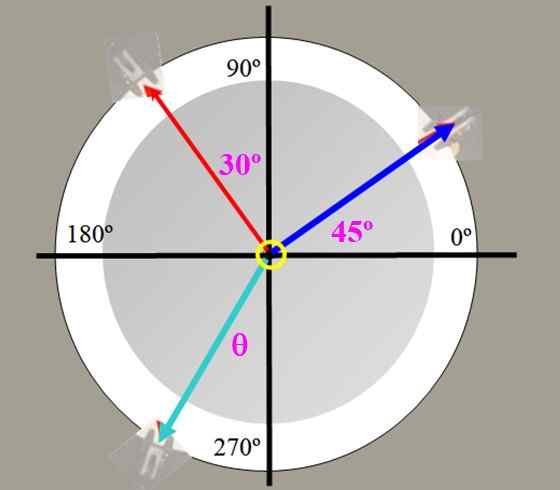
Rajah 2. Lihat dari bahagian atas meja Angkatan. Sumber: Diri Diri.

Dengan jadual daya, anda boleh mengesahkan watak vektor daya, menguraikan kuasa, mencari daya mengimbangi dan mengesahkan teorem Lamy:

Boleh melayani anda: matahari

Sekiranya Tubuh berada dalam keseimbangan terima kasih kepada tiga pasukan coplanar, serentak dan tidak -kolineal (bukan parallel), yang dipanggil Ke, B dan C, Hubungan antara kekuatan ini adalah seperti berikut:

A/ SIN α = B/ SEN β = C/ SEN γ

Rajah 3. Teorem Lamy terpakai kepada pasukan serentak dan coplanar. Sumber: Wikimedia Commons.

Latihan yang diselesaikan

-Latihan 1

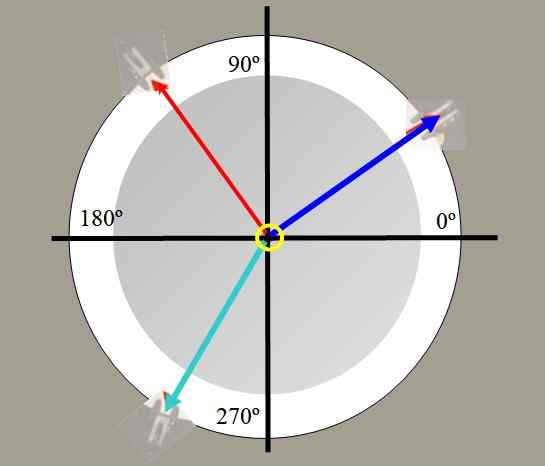
Dalam jadual kuasa dalam Rajah 2 berat 225 g (ketegangan biru) dan 150 g (ketegangan merah) digantung, dengan sudut ditunjukkan. Cari nilai daya mengimbangi dan sudut yang bentuk ini dengan paksi menegak.

Rajah 4. Jadual Angkatan untuk Latihan 1.

Penyelesaian

Masalahnya boleh dilakukan dengan berat yang dinyatakan dalam gram (kuasa). Biarkan p₁ = 150 gram dan p₂ = 225 gram, komponen masing -masing adalah:

P_1x = 225 . cos 45º g = 159.10 g; P_1y = 225 . cos 45º g = 159.10 g

P_2x = -150 . Sen 30º g = -75.00 g; P_{2 dan} = 150 . Cos 30º g = 129.90 g

Berat yang terhasil P_R Komponennya secara algebra menambah:

P_Rx = 159.10 - 75.00 g = 84.10 g

P_Ry = 159.10 + 129.90 g = 289.00 g

Berat badan P_Dan adalah vektor yang bertentangan P_R:

P_Ex = -84.10 g

P_Hey = -289.00 g

Besarnya berat mengimbangi dikira oleh:

P_Dan = (Ms_Ex² + P_Hey²)^1/2 = ((-84.10)² + (-289.00)²)^1/2 G = 301 g

Sudut θ dari angka adalah:

θ = arctg (-84.10 / -289.00) = 16.Ke -2 berkenaan dengan paksi dan negatif.

-Latihan 2

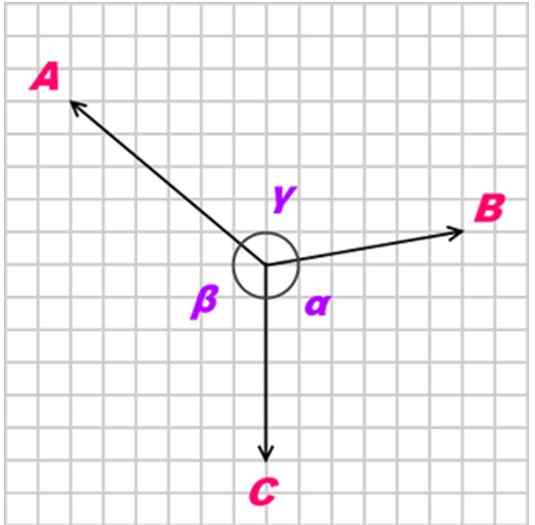
Cari vektor pengimbangan sistem yang ditunjukkan dalam angka tersebut, mengetahui bahawa setiap persegi mengukur 10 m sisi.

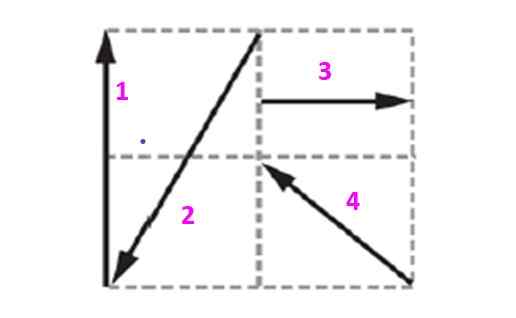Rajah 5. Rajah untuk contoh yang diselesaikan 2.

Penyelesaian

Vektor yang terkandung dalam grid ini akan dinyatakan dari segi unit dan vektor ortogonal Yo dan J yang menentukan kapal terbang. Vektor 1, yang akan dilambangkan sebagai v₁ Ia mempunyai magnitud 20 m dan diarahkan secara menegak ke atas. Ia boleh dinyatakan sebagai:

Ia boleh melayani anda: pemindahan haba radiasi (dengan contoh)

v₁ = 0 Yo +dua puluh J m

Dari lukisan itu diperhatikan bahawa vektor 2 adalah:

v₂ = -10 Yo - dua puluh J m

Vektor 3 adalah mendatar dan mata dalam alamat positif:

v₃ = 10 Yo + 0 J  m

Akhirnya, vektor 4 cenderung 45 º, kerana ia adalah pepenjuru persegi, oleh itu komponennya mengukur sama:

v₄ = -10 Yo + 10 J m

Perhatikan bahawa tanda -.

Vektor yang dihasilkan diperoleh dengan menambahkan komponen komponen:

v_R = -10 Yo + 10 J m

Kemudian vektor pengimbangan sistem adalah:

v_Dan = 10 Yo - 10 J m

Rujukan

1. Beardon, t. 2011. Pengenalan kepada vektor. Pulih dari: nrich.Matematik.org.
2. Bedford, 2000. Ke. Mekanik untuk Kejuruteraan: Statik. Addison Wesley. 38-52.
3. Figueroa, d. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik.31-68.
4. Fizikal. Modul 8: vektor. Pulih dari: frtl.Utn.Edu.ar
5. Hibbeler, R. 2006. Mekanik untuk jurutera. Statik. Edisi ke -6. Syarikat Editorial Continental. 15-53.
6. Vektor kalkulator tambahan. Pulih dari: 1728.org
7. Vektor. Pulih dari: Wikibooks.org