Vektor di Angkasa Cara Graf, Aplikasi, Latihan

A vektor di ruang angkasa Semuanya diwakili oleh sistem koordinat yang diberikan oleh x, dan dan z. Hampir selalu kapal terbang Xy Ia adalah satah permukaan mendatar dan paksi z mewakili ketinggian (atau kedalaman).

Paksi koordinat Cartesian yang ditunjukkan dalam Rajah 1, bahagikan ruang menjadi 8 wilayah yang dipanggil Octavers, sama dengan bagaimana paksi x - dan Bahagikan pesawat ke 4 kuadran. Kami kemudian akan mempunyai 1 Octant, 2nd Ocanto dan sebagainya.

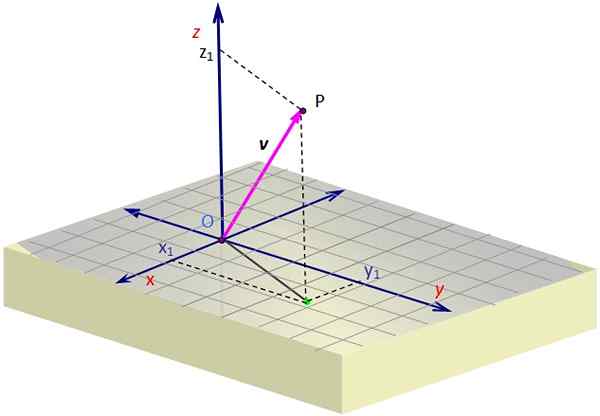
Rajah 1. Vektor di angkasa. Sumber: Diri Diri.

Rajah 1 mengandungi perwakilan vektor v di ruang angkasa. Sesetengah perspektif diperlukan untuk mencipta ilusi tiga dimensi pada satah skrin, yang dicapai dengan melukis pandangan serong.

Untuk graf vektor 3D, anda perlu membantu garis putus -putus yang menentukan koordinat unjuran atau "bayangan" grid v Di atas permukaan x-dan. Unjuran ini bermula di O dan berakhir di titik hijau.

Sekali di sana anda perlu meneruskan dengan menegak ke ketinggian (atau kedalaman) yang diperlukan mengikut nilai z, Sehingga anda sampai ke P. Vektor diambil dari o dan berakhir di p, yang dalam contohnya berada di ocant pertama.

[TOC]

Aplikasi

Vektor di angkasa digunakan secara meluas dalam mekanik dan cabang fizik dan kejuruteraan lain, kerana struktur yang mengelilingi kita memerlukan geometri dalam tiga dimensi.

Vektor kedudukan di ruang digunakan untuk meletakkan objek berkenaan dengan titik rujukan yang dipanggil asal Sama ada. Oleh itu mereka juga alat yang diperlukan dalam navigasi, tetapi itu bukan semua.

Boleh melayani anda: Gelombang elektromagnet: Teori, Jenis, Ciri -ciri Maxwell

Kekuatan yang bertindak ke atas struktur seperti bolt, sokongan, kabel, struts dan banyak lagi adalah sifat vektor dan berorientasikan di angkasa. Untuk mengetahui kesannya, perlu mengetahui alamat anda (dan juga titik permohonan anda).

Dan kerap arah daya dikenali oleh dua titik di ruang yang tergolong dalam garis tindakannya. Dengan cara ini kekuatannya adalah:

F = F atau

Di mana f adalah magnitud atau modul daya dan atau Ia adalah vektor unit (modul 1) yang diarahkan sepanjang garis tindakan F. 

Notasi dan Perwakilan Vektor 3D

Sebelum menyelesaikan beberapa contoh, notasi vektor 3D akan dikaji secara ringkas.

Dalam contoh Rajah 1, vektor V, yang titik asalnya bertepatan dengan asal atau dan yang berakhir adalah titik p, mempunyai koordinat x dan z positif, semasa menyelaras dan Ia negatif. Koordinat ini adalah: x₁, dan₁, z₁, yang tepat koordinat p.

Oleh itu, jika kita mempunyai vektor yang dikaitkan dengan asal, iaitu titik permulaannya bertepatan dengan O, sangat mudah untuk menunjukkan koordinatnya, yang akan menjadi titik yang melampau atau p. Untuk membezakan antara satu titik dan vektor, kami akan menggunakan huruf dan kurungan yang terkini, seperti ini:

v = < x₁, dan₁, z₁ >

Walaupun Point P dilambangkan dengan tanda kurung:

P = (x₁, dan₁, z₁)

Perwakilan lain menggunakan vektor unit Yo, J dan k yang menentukan tiga arah ruang di paksi x, dan dan z masing -masing.

Vektor ini berserenjang antara satu sama lain dan membentuk a Asas Ortonormal (Lihat Rajah 2). Ini bermakna bahawa vektor 3D boleh ditulis dari segi mereka sebagai:

Boleh melayani anda: pergerakan bergelora: ciri, jenis gelombang, contoh

v = v_x Yo + v_dan J + v_z k

Pengarah sudut dan cosenos vektor

Rajah 2 juga menunjukkan sudut pengarah γ₁, γ₂ dan γ₃ daripada vektor v masing -masing dengan paksi x, dan dan z. Mengetahui sudut -sudut ini dan magnitud vektor, ini ditentukan sepenuhnya. Di samping itu, kosines para pengarah memenuhi hubungan berikut:

(cos γ₁)² + (cos γ₂)² + (cos γ₃)² = 1

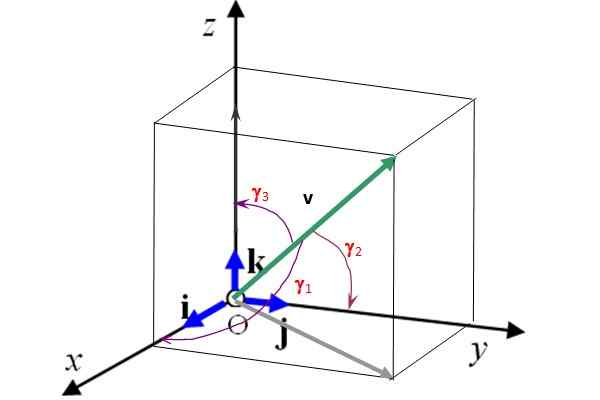Rajah 2. Vektor UNISTAR I, J dan K Tentukan 3 arah keutamaan ruang. Sumber: Diri Diri.

Latihan yang diselesaikan

-Latihan 1

Dalam Rajah 2 sudut γ₁, γ₂ dan γ₃ daripada vektor v bentuk modul 50 dengan paksi koordinat masing -masing: 75.0º, 60.0º dan 34.Ke -3. Cari komponen Cartesian vektor ini dan mewakilinya dari segi vektor unit Yo, J dan k.

Penyelesaian

Unjuran vektor v pada paksi x adalah v_x = 50 . Cos 75º = 12.941. Begitu juga unjuran v pada paksi dan adalah v_dan = 50 cos 60 º = 25 dan akhirnya pada paksi z adalah v_z = 50. cos 34.3 = 41.3. Sekarang v boleh dinyatakan sebagai:

v = 12.9 Yo + 25.0 J + 41.3 k

-Latihan 2 

Cari ketegangan dalam setiap kabel yang memegang baldi angka yang berada dalam keseimbangan, jika beratnya adalah 30 n.

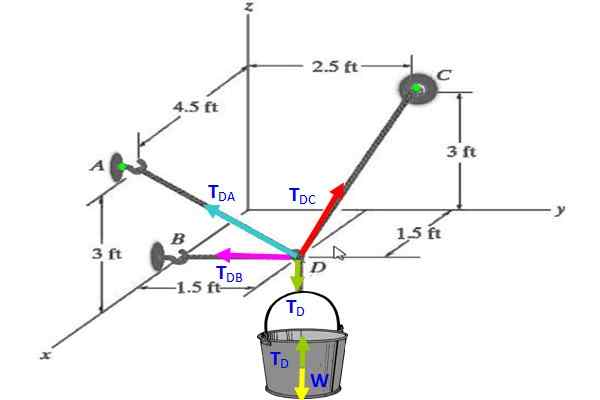Rajah 3. Rajah Ketegangan untuk Latihan 2.

Penyelesaian

Di baldi, gambarajah badan bebas menunjukkan bahawa T_D (hijau) mengimbangi berat badan W (kuning), oleh itu t_D = W = 30 n.

Di simpul, vektor T_D  Ia diarahkan secara menegak, kemudian:

T_D = 30 (-k) N.

Untuk mewujudkan ketegangan yang selebihnya, anda perlu mengikuti langkah -langkah berikut:

Langkah 1: Cari koordinat semua mata

A = (4.5; 0; 3) (A ada di atas kapal terbang X-Z)

B = (1.5; 0; 0) (b ada pada paksi x)

Boleh melayani anda: alamat (fizikal)

C = (0, 2.5, 3) (c di atas kapal terbang dan z)

D = (1.5; 1.5; 0) (D berada di atas kapal terbang mendatar  x-dan)

Langkah 2: Cari vektor di setiap arah dengan menolak koordinat akhir dan permulaan

Memberi =

DC =

Db =

Langkah 3: Kirakan modul dan vektor unit

Vektor unit diperoleh dengan ungkapan: atau = r / r, dengan r (berani) menjadi vektor dan r (tanpa berani) modul vektor tersebut.

Da = (3² + (-1.5)² + 3²)^½ = 4.5; Dc = ((-1.5) ² + 1² + 3²)^½ = 3.5

atau_Memberi = 4.5 =

atau_DC = 3.5 =

atau_Db =

atau_D =

Langkah 4: Ekspresikan semua ketegangan sebagai vektor

T_Memberi = T_Memberi atau_Memberi = T_Memberi

T_DC = T_DC atau_{Dc =}  T_DC

T_Db = T_Db atau_Db = T_Db

 T_D = 30

Langkah 5: Gunakan keadaan keseimbangan statik dan selesaikan sistem persamaan

Akhirnya, keadaan keseimbangan statik digunakan pada baldi, supaya jumlah vektor semua daya pada simpulan adalah tidak sah:

T_Memberi + T_DC + T_Db + T_D = 0

Oleh kerana ketegangan berada di angkasa, ia akan membawa kepada tiga sistem persamaan untuk setiap komponen (x, dan dan z) ketegangan.

0.67 t_Memberi -0.43 t_DC + 0 t_Db = 0

-0.33 t_Memberi + 0.29 t_DC - T_Db = 0

0.67 t_Memberi + 0.86 t_DC +0 t_Db - 30 = 0

Penyelesaiannya ialah: t_Memberi = 14.9 n; T_Memberi = 23.3 n; T_Db = 1.82 n

Rujukan

1. Bedford, 2000. Ke. Mekanik untuk Kejuruteraan: Statik. Addison Wesley. 38-52.
2. Figueroa, d. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik.31-68.
3. Fizikal. Modul 8: vektor. Pulih dari: frtl.Utn.Edu.ar
4. Hibbeler, R. 2006. Mekanik untuk jurutera. Statik. Edisi ke -6. Syarikat Editorial Continental. 15-53.
5. Vektor kalkulator tambahan. Pulih dari: 1728.org