Vektor Colineal

Kami menerangkan apa vektor colineal, sistem vektor colineal dan kami meletakkan beberapa contoh

Apakah vektor kollineal?

The Vektor Colineal Mereka adalah salah satu daripada tiga jenis vektor sedia ada. Ini adalah vektor yang berada dalam arah yang sama atau garis tindakan. Ini bermaksud yang berikut: Dua atau lebih vektor akan menjadi Colineal jika ada kes yang disusun dalam garis yang selari antara satu sama lain.

Vektor ditakrifkan sebagai magnitud yang digunakan pada badan dan dicirikan dengan mempunyai arah, rasa dan skala. Vektor boleh didapati dalam satah atau di ruang angkasa dan boleh menjadi pelbagai jenis: vektor colineal, vektor serentak dan vektor selari.

Bilakah terdapat vektor kollineal?

Vektor adalah colineal jika garis tindakan seseorang adalah garis tindakan yang sama dari semua vektor lain, tanpa mengira saiz dan arah setiap vektor.

Vektor digunakan sebagai representasi dalam pelbagai bidang seperti matematik, fizik, algebra dan juga dalam geometri, di mana vektor adalah colineal hanya apabila arah mereka sama, tanpa mengira maksudnya.

Contoh vektor colineal

• Dua atau lebih vektor adalah colineal jika hubungan antara koordinat adalah sama.

Contoh 1

Anda mempunyai vektor m = m_x; m_y dan n = n_x; N_. Ini adalah collinear jika:

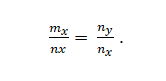
Contoh 2

Ia boleh ditentukan jika vektor j = 3,6,15 dan p = 1,2,5 adalah collinear melalui hubungan koordinat mereka, yang mana anda mesti berkadar antara satu sama lain; iaitu: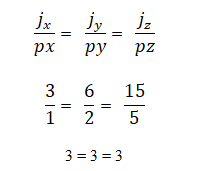

• Dua atau lebih vektor adalah colineal jika pendaraban produk atau vektor sama dengan sifar (0). Ini kerana, dalam sistem koordinat, setiap vektor dicirikan oleh koordinat masing -masing, dan jika ini berkadar antara satu sama lain, vektor akan menjadi collinear. Ini dinyatakan seperti berikut:

Boleh melayani anda: set setara: Apa, penjelasan, contoh

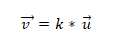
Contoh 1

Anda mempunyai vektor a = (10, 5) dan b = (6, 3). Untuk menentukan sama ada mereka adalah Colineal, teori penentuan digunakan, yang menetapkan kesamaan produk silang. Dengan cara ini, anda mesti:

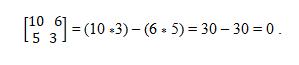
Sistem vektor Colineal

Vektor Colineal diwakili secara grafik menggunakan arah dan arah ini - dengan mengingati bahawa ini mesti melalui titik permohonan - dan modul, yang merupakan skala atau panjang tertentu.

Sistem vektor colineal dibentuk apabila dua atau lebih vektor bertindak pada objek atau badan, yang mewakili daya dan bertindak ke arah yang sama.

Contohnya, jika dua daya colineal digunakan pada badan, yang dihasilkan hanya bergantung kepada pengertian di mana mereka bertindak. Terdapat tiga kes, iaitu:

Vektor colineal dengan deria bertentangan

Hasil dua vektor colineal adalah sama dengan jumlah ini:

R = Σ f = f₁ + F_2.

Contoh

Sekiranya dua pasukan F bertindak di atas kereta₁ = 40 n dan f₂ = 20 n ke arah yang bertentangan (seperti yang ditunjukkan dalam imej), hasilnya ialah:

R = Σ f = (- 40 n) + 20n.

R = - 20 n.

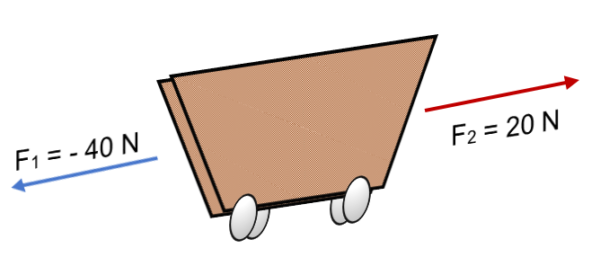Tanda negatif menyatakan bahawa badan akan bergerak ke kiri, dengan kekuatan bersamaan dengan 20 n.

Vektor colineal dalam erti kata yang sama

Besarnya daya yang dihasilkan akan sama dengan jumlah vektor colineal:

R = Σ f = f₁ + F_2.

Contoh

Sekiranya dua pasukan F bertindak di atas kereta₁ = 35 N dan F₂ = 55 n ke arah yang sama (seperti yang ditunjukkan dalam imej), hasilnya ialah:

R = Σ f = 35 n + 55n.

R = 90 n.

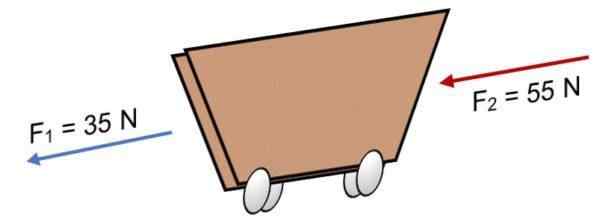
Hasil positif menunjukkan bahawa vektor kollineal bertindak ke kiri.

Ia boleh melayani anda: Peraturan T: Ciri -ciri, supaya ia, contohnya

Vektor colineal dengan magnitud yang sama dan deria bertentangan

Hasil dari kedua -dua vektor collineal akan sama dengan jumlah vektor collinear:

R = Σ f = f₁ + F_2.

Oleh kerana daya mempunyai magnitud yang sama tetapi dalam arah yang bertentangan -iaitu, yang akan menjadi positif dan satu lagi negatif -, dengan menambahkan kedua -dua daya hasilnya akan sama dengan sifar.

Contoh

Sekiranya dua pasukan F bertindak di atas kereta₁ = -7 n dan f₂ = 7 n, yang mempunyai magnitud yang sama, tetapi dalam arah yang bertentangan (seperti yang ditunjukkan dalam imej), hasilnya adalah:

R = Σ f = (-7 n) + 7n.

R = 0.

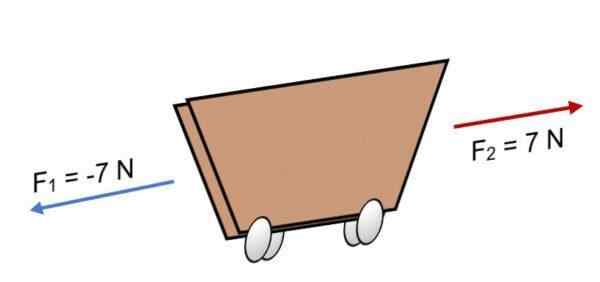
Hasilnya sama dengan 0, ini bermakna bahawa vektor keseimbangan antara satu sama lain dan, oleh itu, badan adalah seimbang atau berehat (ia tidak akan bergerak).

Perbezaan antara vektor colineal dan serentak

Vektor Colineal dicirikan dengan mempunyai arah yang sama pada baris yang sama, atau kerana ia selari dengan garis; Iaitu, mereka adalah vektor pengarah garis selari.

Bagi mereka, vektor serentak ditakrifkan kerana mereka berada dalam pelbagai tindakan yang dipintas pada satu titik.

Dalam erti kata lain, mereka mempunyai titik asal atau ketibaan yang sama -tanpa mengira modul, makna atau arah mereka -membentuk sudut di antara mereka.

Sistem vektor serentak diselesaikan oleh kaedah matematik atau grafik, yang merupakan kaedah parallelogram daya dan kaedah poligon daya. Melalui ini, nilai vektor yang dihasilkan akan ditentukan, yang menunjukkan arah di mana badan akan bergerak.

Pada asasnya, perbezaan utama antara vektor collinear dan serentak adalah garis tindakan di mana mereka bertindak: collineals bertindak dalam garis yang sama, sementara yang bersamaan dengan yang berbeza.

Boleh melayani anda: Sistem Persamaan: Kaedah Penyelesaian, Contoh, Latihan

Iaitu, vektor collinear bertindak dalam satu pesawat, "x" atau "y"; Dan tindakan serentak dalam kedua -dua pesawat, bermula dari titik yang sama.

Vektor Colineal tidak pada satu ketika, seperti yang dilakukan bersamaan, kerana mereka selari antara satu sama lain.

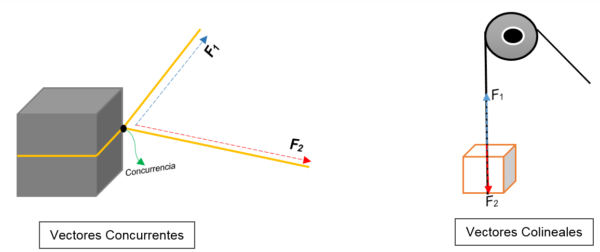
Di sebelah kiri anda dapat melihat blok. Ia terikat dengan tali dan simpul membahagikannya kepada dua; Apabila ditemui ke arah orientasi yang berbeza dan dengan daya yang berbeza, blok akan bergerak ke arah yang sama.

Dua vektor diwakili pada satu titik (blok), tanpa mengira modul, arah atau arah mereka.

Sebaliknya, dengan imej yang betul, pulley muncul yang mengangkat kotak. Tali mewakili garis tindakan; Apabila ia dihentikan, dua pasukan (vektor) bertindak di atasnya: daya ketegangan (ketika memanjat blok) dan kekuatan lain, yang menimbulkan berat blok. Kedua -duanya mempunyai arah yang sama, tetapi dalam deria bertentangan; Mereka tidak bersetuju pada satu ketika.