Definisi vektor yang melengkapkan, notasi, latihan

Dua atau lebih Vektor adalah peralatan Sekiranya mereka mempunyai modul yang sama, arah yang sama dan akal yang sama, walaupun titik asalnya berbeza. Ingat bahawa ciri -ciri vektor adalah tepat: asal, modul, arah dan rasa. 

Vektor diwakili oleh segmen berorientasikan atau anak panah. Rajah 1 menunjukkan perwakilan beberapa vektor dalam satah, yang sebahagiannya adalah peralatan mengikut definisi yang pada mulanya diberikan.

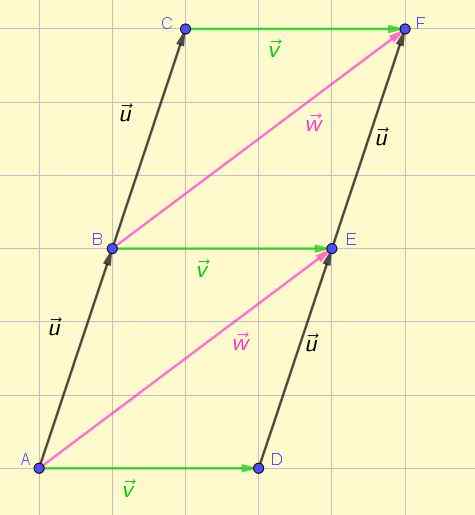Rajah 1. Peralatan dan vektor bukan selekoh. Sumber: Diri Diri.

Dari pandangan pertama adalah mungkin untuk menghargai bahawa tiga vektor hijau mempunyai saiz yang sama, arah yang sama dan rasa yang sama. Perkara yang sama boleh disahkan mengenai dua vektor merah jambu dan empat vektor hitam.

Banyak magnitud alam mempunyai tingkah laku vektor, seperti halnya kelajuan, pecutan dan kekuatan, untuk menamakan hanya beberapa. Oleh itu pentingnya mencirikan mereka dengan betul.

[TOC]

Notasi untuk vektor dan peralatan

Untuk membezakan jumlah vektor jumlah skalar, huruf jenis hitam atau anak panah pada huruf sering digunakan. Semasa bekerja dengan vektor tangan, pada buku nota, perlu membezakannya dengan anak panah dan apabila medium bercetak digunakan, yang berani digunakan.

Vektor boleh dinafikan menunjukkan titik permulaan atau asal mereka dan titik ketibaan mereka. Sebagai contoh Ab, BC, Dari dan Ef Rajah 1 adalah vektor Ab, BC, Dari dan Ef Mereka adalah kuantiti skalar atau nombor yang menunjukkan magnitud, modul atau saiz vektor masing -masing.

Untuk menunjukkan bahawa dua vektor adalah peralatan, simbol digunakan "~ ". Dengan notasi ini, dalam angka kita dapat menunjukkan vektor berikut yang merupakan peralatan antara satu sama lain:

Boleh melayani anda: Tenaga Kinetik: Ciri, Jenis, Contoh, Latihan

Ab ~ bc ~ de ~ ef 

Mereka semua mempunyai magnitud, arah dan makna yang sama. Oleh itu mematuhi peraturan yang dinyatakan di atas.

Vektor percuma, gelongsor dan bertentangan

Mana -mana vektor dalam angka (contohnya Ab) adalah wakil set semua vektor tetap tetap. Set tak terhingga ini mentakrifkan kelas vektor percuma atau.

atau = AB, BC, dari, ef, ..

Notasi alternatif adalah seperti berikut:

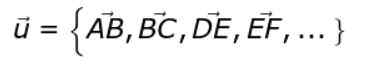
Sekiranya anak panah atau anak panah tidak diletakkan di atas atau, Kami mahu merujuk kepada modul vektor atau.

Vektor percuma tidak digunakan untuk beberapa titik tertentu.

Untuk bahagian mereka Vektor gelongsor Mereka adalah peralatan peralatan ke vektor tertentu, tetapi titik permohonan mereka mesti terkandung dalam talian tindakan vektor.

Dan juga vektor bertentangan Mereka adalah vektor yang mempunyai magnitud dan arah yang sama tetapi deria yang bertentangan, walaupun dalam teks bahasa Inggeris mereka dipanggil Alamat bertentangan Oleh kerana alamat juga menunjukkan makna. Vektor yang bertentangan bukan peralatan.

Latihan

-Latihan 1

Vektor lain yang ditunjukkan dalam Rajah 1 adalah peralatan antara satu sama lain?

Penyelesaian

Selain daripada yang telah ditunjukkan dalam bahagian sebelumnya, diperhatikan dari Rajah 1 bahawa AD, Menjadi dan Ec Mereka juga melengkapkan vektor antara satu sama lain:

AD ~ BE ~ CE 

Mana -mana daripada mereka adalah wakil kelas vektor percuma v.

Vektor juga peralatan di antara mereka Ae dan Bf :

Ae ~ Bf 

Yang merupakan wakil kelas W.

-Latihan 2

Mata A, B dan C berada di Plane XY Cartesian dan koordinat mereka adalah:

Boleh melayani anda: gas ideal: model, tingkah laku, contoh

A = (-4.1), b = (-1.4) dan c = (-4, -3)

Cari koordinat titik keempat d supaya vektor Ab dan CD Menjadi peralatan.

Penyelesaian 

Jadi itu CD menjadi peralatan Ab mesti mempunyai modul yang sama dan arah yang sama seperti Ab .

Modul Ab Persegi adalah:

|Ab|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

D koordinat tidak diketahui untuk apa yang boleh kita katakan: d = (x, y)

Kemudian: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

Sebagai |Ab| = |CD| Ia adalah salah satu syarat untuk Ab dan CD Menjadi peralatan yang anda ada:

(x + 4)^2 + (y + 3)^2 = 18

Oleh kerana terdapat dua orang yang tidak diketahui, persamaan lain diperlukan, yang dapat dicapai dari keadaan itu Ab dan CD selari dan dalam erti kata yang sama.

Vektor ab cerun

Cerun vektor Ab Menunjukkan alamat anda:

Menunggu ab = (4 -1)/(-1 -( -4)) = 3/3 = 1

Menunjukkan bahawa vektor Ab Borang 45º dengan paksi x.

Cerun vektor CD

Cerun CD Ia dikira sama:

Cd yang belum selesai = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Memadankan hasil ini dengan cerun Ab Anda mempunyai persamaan berikut:

Y + 3 = x + 4 

Yang bermaksud y = x + 1.

Jika hasil ini digantikan dalam persamaan kesamaan modul, ia adalah:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Memudahkan adalah:

2 (x+4)^2 = 18, 

Yang bersamaan dengan:

(x+4)^2 = 9

Iaitu x+4 = 3 yang menunjukkan bahawa x = -1. Supaya koordinat d adalah (-1, 0).

periksa

Komponen vektor Ab Mereka adalah (-1-(-4); 4 -1) = (3; 3)

Boleh melayani anda: Teorem Thévenin: Apa yang terdiri, aplikasi dan contoh

dan vektor CD Mereka adalah (-1-(-4)); 0 -(-3)) = (3; 3)

Yang bermaksud bahawa vektor adalah peralatan. Sekiranya dua vektor mempunyai komponen Cartesian yang sama mempunyai modul dan arah yang sama, oleh itu ia adalah peralatan.

-Latihan 3

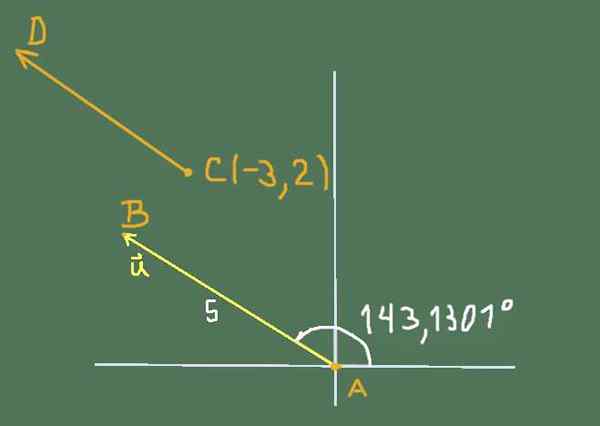
Vektor percuma atau mempunyai magnitud 5 dan alamat 143,1301º.

Cari komponen Cartesiannya dan tentukan koordinat titik b dan c mengetahui bahawa vektor tetap AB dan CD adalah peralatan. Koordinat A adalah (0, 0) dan koordinat titik C ialah (-3,2).

Penyelesaian 

Keadaan yang dicadangkan oleh latihan boleh diwakili oleh angka berikut:

Rajah 2. Rajah untuk Resolusi Latihan 3. Sumber: Diri Diri.

Komponen Cartesian atau adalah

atau = (5*cos (143,1301º); 5*dosa (143,1301º)) 

Membuat pengiraan kekal:

atau = (-4; 3) 

Koordinat b tidak diketahui, jadi kami akan meletakkan b (x, y)

Koordinat vektor Ab Mereka adalah (X-0; Y-0), tetapi kerana peralatan dengan U mesti dipenuhi kesamaan komponen, oleh itu disimpulkan bahawa koordinat B adalah (-4, 3).

Begitu juga koordinat vektor CD Mereka adalah (x-(-3)); (dan - 2) Itu mesti peralatan u, latau yang membawa kepada:

 x + 3 = -4 dan y -2 = 3

Maka koordinat titik D akan (-7, 5).

Rujukan

1. Pengiraan.DC. Vektor tetap. Vektor percuma. Pulih dari: pengiraan.DC
2. 2d Descartes. Vektor tetap dan vektor percuma pesawat. Diperolehi dari: Sumber.pendidikan.adalah
3. Projek GUAO. Melengkapkan vektor. Pulih dari: guao.org
4. Resnick, r., Krane, k. (2001). Fizik (dalam bahasa Inggeris). New York: John Wiley & Sons.
5. Serway, r.; Jewett, John W. (2004). Fizik untuk saintis dan jurutera (dalam bahasa Inggeris) (edisi ke -6). Brooks/Cole.
6. Tupler, Paul a. (2000). Fizik untuk Sains dan Teknologi. Jilid I. Barcelona: Ed. Saya terbalik.
7. Weisstein, e. "Vektor". Di Weisstein, Eric W. MathWorld (dalam bahasa Inggeris). Penyelidikan Wolfram.