Definisi, syarat, latihan vektor bukan vektor

The Vektor bukan -coplanar Mereka adalah mereka yang tidak berkongsi pesawat yang sama. Dua vektor percuma dan satu titik menentukan satah tunggal. Vektor ketiga mungkin atau tidak boleh berkongsi pesawat itu dan jika tidak, ini adalah vektor bukan -planar.

Vektor bukan -couplet tidak boleh diwakili dalam ruang dua dimensi seperti papan atau lembaran kertas, kerana beberapa di antaranya terkandung dalam dimensi ketiga. Untuk mewakili mereka dengan betul, anda mesti menggunakan perspektif.

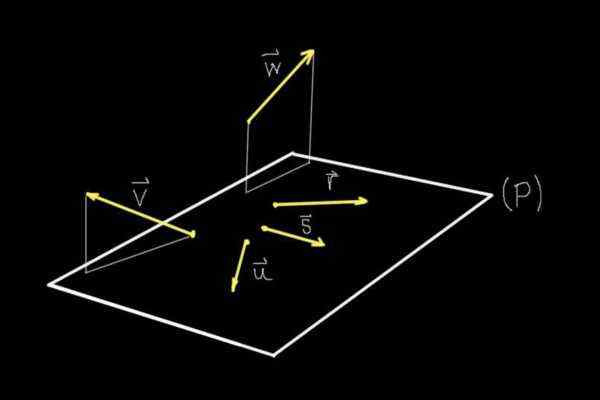Rajah 1. Vektor coplanares dan bukan gandingan. (Huraian sendiri)

Sekiranya kita melihat Rajah 1, semua objek yang ditunjukkan dengan ketat berada dalam satah skrin, namun terima kasih kepada perspektif otak kita dapat membayangkan pesawat (p) yang keluar dari yang sama.

Di pesawat itu (p) adalah vektor r, s, atau, sementara vektor v dan W  Mereka tidak berada di kapal terbang itu.

Oleh itu vektor r, s, atau Mereka adalah coplanarios atau coplanares antara satu sama lain kerana mereka berkongsi pesawat yang sama (p). Vektor v dan W Mereka tidak berkongsi flat dengan mana-mana vektor lain yang ditunjukkan, oleh itu mereka bukan gandingan. 

[TOC]

Vektor persamaan coplanares dan kapal terbang

Pesawat ditakrifkan secara unik jika tiga mata diberikan dalam ruang tiga dimensi.

Katakan tiga mata itu adalah titik Ke, titik B dan titik C yang menentukan pesawat (P). Dengan mata ini adalah mungkin untuk membina dua vektor AB = U dan Ac = v dengan pembinaan dengan kapal terbang (P).

Produk vektor (atau produk silang) dari kedua -dua vektor ini menghasilkan vektor serenjang (atau normal) ketiga kepada mereka dan oleh itu tegak lurus ke satah (P):

n = u X v   => n ⊥ atau  dan n ⊥ v   => n ⊥ (P)    

Boleh melayani anda: Berat (fizikal): pengiraan, unit, contoh, latihan

Mana -mana titik lain yang dimiliki oleh kapal terbang (P) mesti memenuhi bahawa vektor Aq berserenjang dengan vektor n; Ini bersamaan dengan mengatakan bahawa produk skalar (atau produk titik) n dengan Aq Mesti sifar:

n • Aq = 0 (*)

Keadaan sebelumnya bersamaan dengan mengatakan bahawa:

Aq • (atau X v) = 0 

Persamaan ini memastikan bahawa Q tergolong dalam kapal terbang (P). 

Persamaan Cartesian pesawat

Persamaan sebelumnya boleh ditulis dengan cara Cartesian. Untuk ini kita menulis koordinat mata Ke, Q dan komponen vektor biasa n:

A = (A, B, C)

Q = (x, y, z)

n= (NX, NY, NZ)

Jadi komponen AQ adalah:

Aq= (X-A, Y-B, Z-C)

Keadaan untuk vektor Aq terkandung dalam pesawat (P) Ia adalah keadaan (*) yang kini ditulis seperti ini:

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Mengira produk titik kekal:

NX (X-A) + NY (Y-B) + NZ (Z-B) = 0

Sekiranya ia berkembang dan menyusun semula ia tetap:

NX X + NY Y + NZ Z = NX A + NY B + NZ C

Ekspresi sebelumnya adalah persamaan Cartesian satah (P), bergantung pada komponen vektor biasa ke (P) dan koordinat satu titik Ke yang dimiliki (P).

Syarat untuk tiga vektor menjadi bukan -kopranar

Seperti keadaan yang telah dilihat di bahagian sebelumnya Aq • (atau X v) = 0 menjamin bahawa vektor Aq Ia adalah coplanario a atau dan v.

Sekiranya kita memanggil W kepada vektor Aq Kemudian kita boleh mengesahkan bahawa:

W, atau dan v Mereka adalah coplanares, ya dan hanya jika W • ( atau X v ) = 0.

Keadaan bukan tingkah laku

Sekiranya produk tiga (atau produk bercampur) tiga vektor berbeza dari sifar maka ketiga-tiga vektor itu bukan corong.

Ia boleh melayani anda: Proses Politropik: Ciri, Aplikasi dan Contohnya

Yeah    W • ( atau X v ) ≠ 0 maka vektor u, v, dan w.

Jika komponen Cartesian U, V, V, dan W diperkenalkan keadaan bukan tingkah laku boleh ditulis seperti berikut:

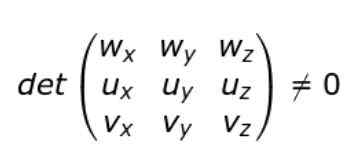Iaitu jika penentu matriks (3 × 3) yang barisnya adalah komponen vektor u, v dan w maka vektor adalah bukan gandingan.

Produk triple mempunyai tafsiran geometri dan mewakili kelantangan paralelepip yang dihasilkan oleh tiga vektor bukan koklanar.

Rajah 2. Tiga vektor bukan gandingan menentukan parallelepipedo yang jumlahnya adalah modul produk tiga. (Huraian sendiri)

Sebabnya adalah seperti berikut; Apabila dua vektor bukan gandingan meningkat. 

Kemudian apabila vektor ini berlipat ganda. 

Dalam erti kata lain, anda mempunyai kawasan paralelogram yang dihasilkan oleh dua yang pertama didarab dengan ketinggian vektor ketiga.

Keadaan alternatif yang tidak digabungkan

Sekiranya anda mempunyai tiga vektor dan mana-mana daripada mereka tidak boleh ditulis sebagai gabungan linear dua yang lain, maka tiga vektor itu bukan. Itu adalah tiga vektor atau, v dan W Mereka bukan cari jika keadaan:

α atau + β v + γ W = 0

Ia hanya dipenuhi apabila α = 0, β = 0 dan γ = 0.

Latihan yang diselesaikan

-Latihan 1

Anda mempunyai tiga vektor

atau = (-3, -6, 2);   v = (4, 1, 0) dan W = (-1, 2, z)

Perhatikan bahawa komponen z vektor W Ia tidak diketahui.

Cari julat nilai yang boleh diambil oleh Z supaya dijamin bahawa tiga vektor tidak berkongsi pesawat yang sama.

Boleh melayani anda: keseimbangan stabil: konsep dan contoh

Penyelesaian 

Kami memohon lagi kriteria penentu matriks yang dibentuk oleh pangkat tiga vektor, dengan cara ini kita tetap: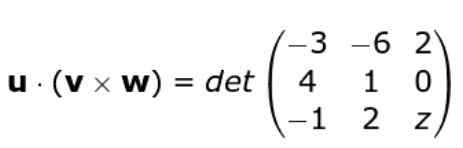Kami membangunkan penentu

W • ( atau X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18

Kami sepadan dengan ungkapan ini pada nilai sifar

21 z + 18 = 0

Dan kita membersihkan z

Z = -18/21 = -6/7

Sekiranya pemboleh ubah z mengambil nilai -6/7 maka tiga vektor akan menjadi coplanares.

Supaya nilai z yang menjamin bahawa vektor adalah bukan cover adalah mereka yang berada dalam selang berikut:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Latihan 2

Cari kelantangan parallelepiped yang ditunjukkan dalam angka berikut:

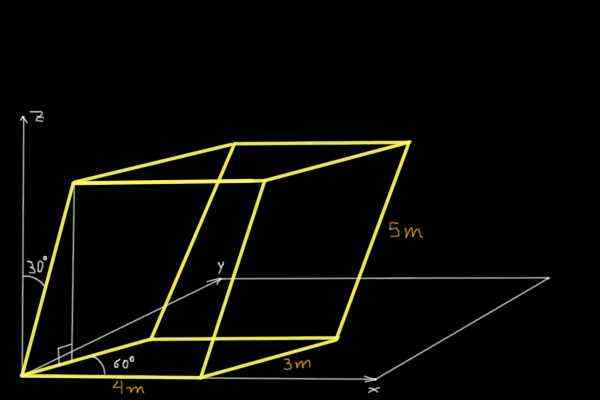
Penyelesaian 

Untuk mencari kelantangan parallelepiped yang ditunjukkan dalam angka itu, komponen Cartesian dari tiga vektor bukan gabungan yang tidak bersekongkol akan ditentukan dalam asal-usul sistem koordinat. Yang pertama adalah vektor atau  4m dan selari dengan paksi x:

atau= (4, 0, 0) m

Yang kedua adalah vektor v Dalam satah saiz 3m XY yang membentuk 60º dengan paksi x:

v= (3*cos 60º, 3*sen 60º, 0) = (1.5, 2.6, 0.0) m

Dan yang ketiga vektor W 5m dan unjurannya dalam satah xy membentuk 60º dengan paksi x, selain bentuk w 30 º dengan paksi z.

W= (5*dosa 30º*cos 60º, 5*sen 30º*dosa 60º, 5*sen 30º)

Menjalankan pengiraan yang kita ada: W= (1.25, 2.17, 2.5m.

Rujukan

1. Figueroa, d. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. 31-68.
2. Fizikal. Modul 8: vektor. Pulih dari: frtl.Utn.Edu.ar
3. Hibbeler, R. 2006. Mekanik untuk jurutera. Statik. Edisi ke -6. Syarikat Editorial Continental.28-66.
4. McLean, w. Siri Schaum. Mekanik untuk Jurutera: Statik dan Dinamik. Edisi ke -3. McGraw Hill. 1-15.
5. Wikipedia. Vektor. Pulih dari: ia adalah.Wikipedia.org