Fizikal

Definisi kelajuan sudut, formula, pengiraan dan latihan

Definisi kelajuan sudut, formula, pengiraan dan latihan

The halaju sudut Ia adalah ukuran kelajuan putaran dan ditakrifkan sebagai sudut yang berputar vektor kedudukan objek yang berputar, per unit masa. Ia adalah magnitud yang menggambarkan pergerakan banyak objek yang sentiasa berpaling di mana -mana: CD, roda kereta, jentera, bumi dan banyak lagi.

Skim "Mata London" dapat dilihat dalam angka berikut. Ia mewakili pergerakan penumpang yang diwakili oleh titik p, yang mengikuti trajektori bulat, yang dipanggil C:

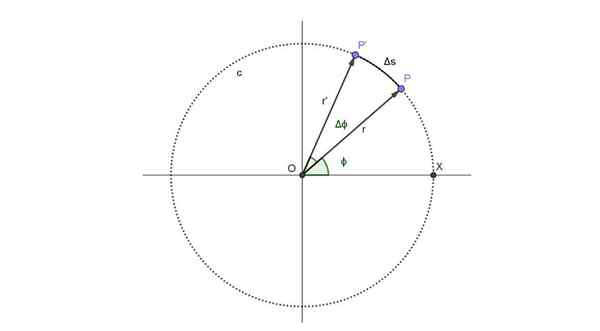Perwakilan skematik trajektori bulat yang mengikuti penumpang "London Eye". Sumber: Diri Diri.

Penumpang menduduki kedudukan p pada masa t dan kedudukan sudut yang sepadan dengan saat itu adalah φ.

Dari saat suatu tempoh masa berlalu ΔT. Dalam tempoh itu kedudukan baru penumpang tepat waktu adalah p 'dan kedudukan sudut telah meningkatkan sudut δφ.

[TOC]

Bagaimana kelajuan sudut dikira ?

Untuk magnitud putaran, huruf Yunani digunakan secara meluas, untuk membezakannya dari magnitud linear. Jadi pada mulanya halaju sudut purata Ω ditakrifkanm Semasa sudut mengembara dalam tempoh masa tertentu.

Maka quient δφ/Δt akan mewakili halaju sudut purata Ωm Antara momen t dan t+Δt.

Sekiranya anda ingin mengira halaju sudut Hanya pada masa t, maka kuota δφ/Δt perlu dikira apabila Δt ➡0:

 Unit ukuran halaju sudut adalah rad/s.

Hubungan antara kelajuan linear dan sudut

Kelajuan linear v, Ia adalah kuota antara jarak perjalanan dan tempoh masa yang digunakan untuk mengembara.

Dalam angka di atas, laluan arka adalah ΔS. Tetapi arka itu berkadar dengan sudut perjalanan dan radius, memenuhi hubungan berikut, yang sah selagi Δφ diukur dalam radian:

Boleh melayani anda: Kaedah Parallelogram: Contoh, Latihan yang Diselesaikan

ΔS = r ・ δφ

Jika kita membahagikan ungkapan sebelumnya antara tempoh masa Δt dan mengambil had apabila Δt ➡0, kita akan mendapat:

v = r ・ Ω

Pergerakan putaran seragam

Foto itu adalah "Eye London" yang terkenal, roda berputar tinggi 135 m yang berputar perlahan -lahan, sehingga orang dapat menaiki kabin di pangkalan mereka dan menikmati landskap London. Sumber: Pixabay.

Pergerakan putaran adalah seragam jika pada bila -bila masa diperhatikan, sudut yang dilalui adalah sama dalam tempoh yang sama.

Sekiranya putaran seragam, maka halaju sudut pada bila -bila masa bertepatan dengan halaju sudut purata.

Dalam pergerakan putaran seragam, masa di mana giliran lengkap dipanggil tempoh dan menandakan dengan t.

Di samping itu, apabila sudut dihidupkan, ia adalah 2π (bersamaan dengan 360º). Itulah sebabnya dalam putaran seragam halaju sudut Ω berkaitan dengan tempoh t, melalui formula berikut:

Kekerapan ditakrifkan F putaran seragam seperti kuota antara jumlah giliran dan masa yang dihabiskan untuk mengembara mereka. Sebagai pulangan 1 ia bergerak dalam masa t (tempoh) mempunyai hubungan berikut:

F = 1/t

Dalam erti kata lain, dalam putaran seragam, halaju sudut berkaitan dengan kekerapan dengan:

Ω = 2π ・ f

Latihan kelajuan sudut diselesaikan

Latihan 1

Kabin roda berputar yang hebat yang dikenali sebagai "Mata London"Mereka bergerak perlahan. Kelajuan kabin adalah 26 cm/s dan roda diameter 135 m.

Dengan data ini hitung:

Boleh melayani anda: matahari

i) halaju sudut roda

ii) kekerapan putaran

iii) Masa yang mengambil kabin untuk berpaling.

Jawapan:

Yo) Kelajuan V dalam m/s ialah: v = 26 cm/s = 0.26 m/s.

Radio adalah separuh daripada diameter: r = (135 m) / 2 = 67.5 m

v = r ・ ω => ω = v/r = (0.26 m/s)/(67.5 m) = 0.00385 rad/s

Ii) Ω = 2π ・ f => f = ω / 2π = (0.00385 rad / s) / (2π rad) = 6.13 x 10-4 bertukar/s

F = 6.13 x 10^-4 giliran/s = 0.0368 giliran/min = 2.21 giliran/jam.

Iii) T = 1 / f = 1/21 giliran / jam = 0.45311 masa = 27 min 11 saat

Latihan 2

Kereta mainan bergerak di landasan bulat 2m jejari. Pada 0 s kedudukan sudutnya adalah 0 rad, tetapi selepas masa t kedudukan sudutnya diberikan oleh:

φ (t) = 2 ・ t 

Tentukan:

i) halaju sudut 

ii) kelajuan linear pada bila -bila masa.

Jawapan:

Yo) Halaju sudut adalah terbitan kedudukan sudut: ω = φ '(t) = 2.

Dalam kata lain.

Ii) Kelajuan linear kereta ialah: V = R ・ Ω = 2 m ・ 2 rad/s = 4 m/s = 14.4 km/j

Latihan 3

Kereta yang sama dari latihan sebelumnya mula berhenti. Kedudukan sudutnya sebagai fungsi masa diberikan oleh ungkapan berikut:

φ (t) = 2 ・ t - 0.5 ・ t2 

Tentukan:

i) halaju sudut pada bila -bila masa

ii) kelajuan linear pada bila -bila masa

iii) masa yang anda ambil untuk berhenti dari saat anda mula menurun

iv) sudut mengembara 

v) Pada jarak yang dilalui

Jawapan:

Yo) Halaju sudut adalah terbitan kedudukan sudut: ω = φ '(t)

Ω (t) = φ '(t) = (2 ・ t - 0.5 ・ t2) '= 2 - t

Ii) Kelajuan linear kereta pada bila -bila masa diberikan oleh:

v (t) = r ・ ω (t) = 2 ・ (2 - t) = 4 - 2 t

Boleh melayani anda: kelajuan relatif: konsep, contoh, latihan

Iii) Masa yang mengambil masa di mana ia mula melambatkan.

V (t) = 4 - 2 t = 0 => t = 2

Itu adalah mengatakan bahawa ia berhenti 2 s setelah mula berhenti.

Iv) Dalam tempoh 2s, dari masa ia mula berhenti sehingga sudut yang diberikan oleh φ (2) dilalui:

φ (2) = 2 ・ 2 - 0.5 ・ 2^2 = 4 - 2 = 2 rad = 2 x 180 / π = 114.6 darjah

V) Dalam tempoh 2 s difahami sejak ia mula berhenti sehingga ia berhenti jarak yang diberikan oleh:

S = r ・ φ = 2m ・ 2 rad = 4 m

Latihan 4

Roda kereta adalah diameter 80 cm. Sekiranya kereta bergerak pada 100 km/j. Cari: i) Kelajuan sudut putaran roda, ii) kekerapan putaran roda, iii) bilangan pusingan yang diberikan roda dalam laluan 1 jam.

Jawapan:

Yo) Di tempat pertama kita akan mengubah kelajuan kereta km/h a m/s

V = 100 km / h = (100/3.6) m/s = 27.78 m/s

Kelajuan putaran roda roda diberikan oleh:

Ω = v/r = (27.78 m/s)/(0.4 m) = 69.44 rad/s

Ii) Kekerapan putaran roda diberikan oleh:

F = ω / 2π = (69.44 rad / s) / (2π rad) = 11.05 giliran / s

Kekerapan putaran biasanya dinyatakan dalam revolusi per minit r.p.m.

F = 11.05 giliran/s = 11.05 giliran/(1/60) min = 663.15 r.p.m

Iii)  Bilangan giliran yang diberikan roda dalam laluan 1 jam, dikira mengetahui bahawa 1 jam = 60 min dan kekerapan adalah bilangan giliran n dibahagikan dengan masa di mana n diberikan.

F = n / t => n = f ・ t = 663.15 (giliran / min) x 60 min = 39788.7 giliran.

Rujukan

  1. Giancoli, d. Fizik. Prinsip dengan aplikasi. Edisi ke -6. Prentice Hall. 106-108.
  2. Resnick, r. (1999). Fizikal. Jilid 1. Edisi ketiga dalam bahasa Sepanyol. Mexico. Syarikat Editorial Continental s.Ke. daripada c.V. 67-69.
  3. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Edisi. Mexico. Editor Pembelajaran Cengage. 84-85.
  4. Geogebra.org