Kelajuan isolar bagaimana ia dikira dan diselesaikan latihan

The Kelajuan isolar Ia adalah kawasan yang menyapu setiap unit masa dan tetap. Ini adalah tipikal dari setiap planet dan timbul dari perihalan undang -undang kedua Kepler dengan cara matematik. Dalam artikel ini kita akan menerangkan apa yang terdiri dan bagaimana ia dikira.

Ledakan yang mewakili penemuan planet di luar sistem solar telah mengaktifkan semula minat dalam pergerakan planet. Tidak ada yang percaya bahawa planet exo ini mengikuti undang-undang selain daripada yang sudah diketahui dan sah sistem solar: Undang-undang Kepler.

Johannes Kepler adalah ahli astronomi yang, tanpa bantuan teleskop dan menggunakan pemerhatian mentornya Tycho Brahe, mencipta model matematik yang menggambarkan pergerakan planet di sekitar matahari.

Dia meninggalkan model ini yang dinyatakan dalam tiga undang -undang yang menanggung namanya dan yang tetap sah hari ini seperti pada tahun 1609, ketika ia menubuhkan dua dan 1618 pertama, tarikh yang ketiga.

[TOC]

Undang -undang Kepler

Dalam bahasa semasa, tiga undang -undang Kepler mengatakan seperti ini:

1. Orbit semua planet adalah elips dan matahari berada dalam fokus.

2. Vektor kedudukan yang pergi dari matahari ke planet menyapu kawasan yang sama dengan masa yang sama.

3. Dataran masa orbit planet adalah berkadar dengan kiub separa ellipse yang diterangkan.

Planet akan mempunyai kelajuan linear, seperti objek yang diketahui yang bergerak. Dan ada lebih banyak lagi: Semasa menulis undang -undang kedua Kepler dalam bentuk matematik, konsep baru yang disebut kelajuan isolar, tipikal setiap planet timbul.

Mengapa planet bergerak elips di sekitar matahari?

Bumi dan planet -planet lain bergerak di sekitar matahari terima kasih kepada hakikat bahawa ia memberi daya pada mereka: tarikan graviti. Begitu juga untuk bintang lain dan planet yang sesuai dengan sistem anda, jika anda memilikinya.

Ia dapat melayani anda: haba sensitif: konsep, formula dan latihan diselesaikan

Ini adalah kekuatan jenis yang dikenali sebagai Pasukan Pusat. Berat adalah kekuatan pusat yang mana semua orang biasa. Objek yang mengerahkan kekuatan pusat, sama ada matahari atau bintang jauh, menarik planet ke arah pusat mereka dan mereka bergerak menerangkan lengkung tertutup.

Pada dasarnya lengkung ini dapat dianggarkan sebagai lilitan, seperti Nicolás Copernico, pencipta astronomi Poland teori heliosentrik,.

Kekuatan yang bertanggungjawab adalah tarikan graviti. Kekuatan ini bergantung secara langsung pada jisim bintang dan planet yang dipersoalkan dan berkadar songsang dengan kuadrat jarak yang memisahkannya.

Masalahnya tidak begitu mudah, kerana dalam sistem solar, semua elemen berinteraksi dengan cara ini, menambah kerumitan kepada perkara itu. Mereka juga bukan zarah, kerana bintang dan planet saiz yang boleh diukur.

Atas sebab ini, titik pusat orbit atau litar yang dilalui oleh planet tidak betul-betul berpusat pada bintang, tetapi pada titik yang dikenali sebagai pusat graviti sistem sol-planet.

Orbit yang dihasilkan adalah elips. Imej berikut menunjukkannya, mengambil sebagai contoh bumi dan matahari:

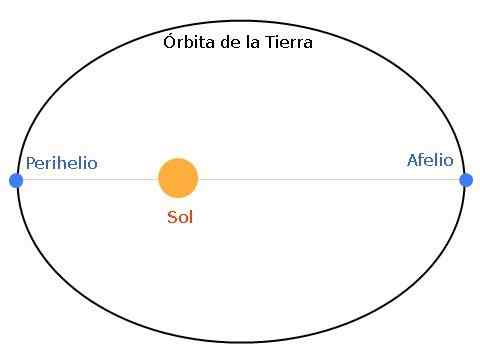Rajah 1. Orbit bumi adalah elips, dengan matahari terletak di salah satu foci. Ketika Bumi dan Matahari berada pada jarak maksimum, dikatakan bahawa bumi ada di aphelium. Dan jika jaraknya minimum maka kita bercakap mengenai perihelio.

Apelium adalah kedudukan paling jauh dari bumi ke matahari, sementara perihelium adalah titik terdekat. Ellipse boleh lebih kurang diratakan, mengikut ciri -ciri sistem bintang - planet.

Nilai asel dan perihelio berbeza -beza setiap tahun, kerana planet lain menyebabkan gangguan. Untuk planet lain, kedudukan ini dipanggil sokongan dan kepakaran masing -masing.

Besarnya kelajuan linear planet tidak tetap

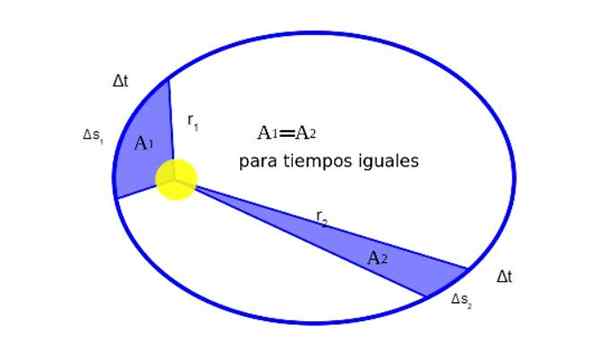
Kepler mendapati bahawa ketika planet mengorbit di sekitar matahari, semasa gerakan Barr sama dengan kawasan yang sama. Rajah 2 secara grafik menunjukkan makna ini:

Ia dapat melayani anda: apakah keseimbangan zarah? (Dengan contoh)Rajah 2. Vektor kedudukan planet berkenaan dengan matahari adalah r. Apabila planet ini menggambarkan orbitnya perjalanan arka elips ΔS dalam masa Δt.

Secara matematik, hakikat bahawa₁ sama dengan₂ Ia dinyatakan seperti ini:

Laluan gerbang kecil, supaya setiap kawasan dapat mendekati segitiga:

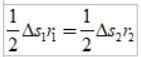
Sebagai ΔS =vΔt, Di mana V adalah kelajuan linear planet ini pada titik tertentu, ketika menggantikan kita mempunyai:

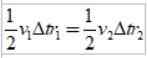
Dan sejak selang waktu Δt adalah sama, ia diperolehi:

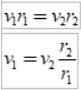
Seperti r₂ > r₁, Kemudian v₁ > v₂, Dengan kata lain, kelajuan linear planet tidak tetap. Malah, bumi akan lebih cepat apabila berada di perihelium daripada ketika berada di aphelium.

Oleh itu, halaju linear bumi atau mana -mana planet di sekeliling matahari bukanlah magnitud yang berfungsi untuk mencirikan pergerakan planet tersebut.

Kelajuan isolar

Undang -undang kedua Kepler mencadangkan magnitud baru yang disebut kelajuan isolar. Ia ditakrifkan sebagai kawasan yang disapu setiap unit masa dan tetap. Untuk mengira, angka berikut digunakan:

Rajah 3. Vektor kedudukan bumi (atau planet) berkenaan dengan matahari adalah r, dan apabila bergerak, bumi mengalami anjakan, juga vektor ΔR.

Kawasan kecil yang disapu oleh Bumi dipilih semasa melakukan litar elipsnya, yang mana kita akan menunjukkan bagaimana ΔA. Masa yang diperlukan untuk ini adalah ΔT.

Rajah 3 menunjukkan vektor kedudukan bumi berkenaan dengan matahari, dilambangkan oleh r. Apabila bumi bergerak, mengalami anjakan ΔR.

Kawasan ini sepadan dengan separuh daripada kawasan segi empat tepat yang ditunjukkan dalam Rajah 3:

Kota ΔR/ΔT adalah tepat halaju linear bumi, jadi kelajuan isolar tetap:

V_Ke Dalam sistem antarabangsa mereka:

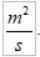
Perhatikan bahawa sementara kedua -dua R dan V berbeza -beza, produk tetap berterusan. Ini menjadikan kelajuan isolar menjadi magnitud yang sangat sesuai untuk mencirikan pergerakan planet di sekitar bintangnya.

Boleh melayani anda: pemalar antoin: formula, persamaan, contoh

Produk R dan V adalah magnitud momentum sudut l, supaya kelajuan isolar dapat dinyatakan sebagai:

Mengira kelajuan linear dan kelajuan isolar

Dengan contoh berikut, kami akan menunjukkan cara mengira kelajuan isolar apabila beberapa parameter pergerakan planet diketahui:

Senaman

Sebuah planet exo bergerak di sekitar matahari berikutan orbit elips, menurut undang-undang Kepler. Apabila ia berada di Expertro, vektor radionya ialah r₁ = 4 · 10⁷ km, dan apabila ia mendapat sokongan adalah r₂ = 15 · 10⁷ km. Kelajuan linear dalam kepakarannya ialah v₁ = 1000 km/s.

Kira:

A) Besarnya kelajuan dalam sokongan.

B) kelajuan isolar exo-planet.

C) Panjang separa ellipse utama.

Jawapan kepada)

Persamaan digunakan:

di mana nilai berangka diganti.

Setiap istilah dikenalpasti seperti berikut:

v₁ = Kelajuan sokongan; v₂ = Kelajuan pakar; r₁= Jarak pengarang,

r₂= Jarak dari pakar.

Dengan nilai -nilai ini diperoleh:

Jawapan b)

Persamaan yang akan digunakan adalah

di mana beberapa nilai r dan v dari expertro atau sokongan boleh diganti, kerana v_Ke Ia adalah planet yang berterusan:

Jawab c)

Panjang separa ellipse utama adalah semi -semi -semi -semi -semi -seismum dan kepakaran:

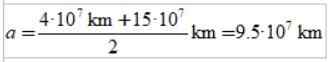
Bibliografi

1. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Mexico. Editor Pembelajaran Cengage. 367-372.
2. Stern, d. (2005). Ketiga Undang -undang Kepler Pergerakan Planet. Diperolehi daripada PWG.GSFC.periuk.Gov
3. Nota: Latihan yang dicadangkan telah diambil dan diubahsuai dari teks buku McGrawhill berikut. Malangnya ia adalah bab terpencil dalam format pdf, tanpa tajuk atau pengarang: mheducation.Es/bcv/panduan/bab/844817027x.Pdf