Definisi kelajuan, formula, pengiraan dan latihan seketika seketika

The kelajuan seketika Ia ditakrifkan sebagai perubahan perpindahan seketika dari masa ke masa. Ia adalah konsep yang menambah ketepatan yang besar dalam kajian pergerakan. Dan ia adalah pendahuluan berkenaan dengan kelajuan purata, yang maklumatnya sangat umum.

Untuk mendapatkan kelajuan seketika, mari kita lihat selang waktu sekecil mungkin. Kalkulus Berbeza adalah alat yang sempurna untuk menyatakan idea ini secara matematik.

Akaun kelajuan seketika untuk kelajuan mudah alih di setiap titik laluannya. Sumber: Pixabay.

Titik permulaan adalah kelajuan purata:

Sekarang mari kita buat pendekatan Δt ke 0 semua yang boleh. Ini adalah had dan hasilnya akan menjadi kelajuan serta -merta:

Had ini dikenali dengan nama terbitan. Dalam notasi kalkulus pembezaan yang anda ada:

Dengan syarat pergerakan itu terhad kepada garis lurus, ia boleh dibekalkan dengan notasi vektor.

[TOC]

Pengiraan Kelajuan Segera: Tafsiran Geometri

Angka berikut menunjukkan tafsiran geometri konsep derivatif: ia adalah cerun garis tangen Ke lengkung x (t) vs. t Pada setiap titik.

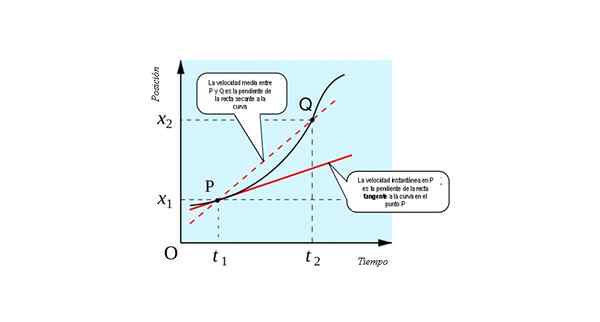Kelajuan seketika dalam p bersamaan dengan numerik ke cerun garis tangen ke lengkung x Vs. t pada titik p. Sumber: Sumber: すじにく シチュー [CC0].

Anda boleh bayangkan bagaimana untuk mendapatkan had jika titik q secara beransur -ansur menghampiri. Akan tiba masanya ketika kedua -dua titik begitu dekat, yang tidak dapat dibezakan dari yang lain.

Garis yang menyatukan mereka kemudian akan mengeringkan (lurus yang memotong menjadi dua mata) menjadi tangen (lurus yang menyentuh lengkung pada satu titik). Oleh itu, untuk mencari kelajuan seketika zarah mudah alih yang sepatutnya kita miliki:

• Graf kedudukan zarah sebagai fungsi masa. Mencari cerun garis tangen ke lengkung pada setiap masa, anda mempunyai kelajuan seketika pada setiap titik yang diduduki oleh zarah.

Boleh melayani anda: Undang -undang Ampère: Formula dan Persamaan, Demonstrasi, Latihan

Wahai:

• Fungsi kedudukan zarah berfungsi x (t), yang diperolehi untuk mendapatkan fungsi kelajuan V (t), Kemudian fungsi ini dinilai pada setiap masa t, Kemudahan. Fungsi kedudukan sepatutnya terburuk.

Beberapa kes khas dalam pengiraan kelajuan serta -merta

-Cerun garis tangen ke lengkung dalam p ialah 0. Cerun null bermaksud bahawa mudah alih dihentikan dan kelajuannya tentu 0.

-Lereng garis tangen ke lengkung di p lebih besar daripada 0. Kelajuannya positif. Dalam graf di atas, ia bermaksud bahawa mudah alih bergerak dari atau.

-Cerun garis tangen ke lengkung di p kurang dari 0. Kelajuan akan negatif. Dalam graf di atas tidak ada mata seperti itu, tetapi dalam hal ini zarah akan menghampiri atau.

-Lereng garis tangen ke lengkung adalah tetap di P dan semua titik lain. Dalam kes ini graf adalah garis lurus dan telefon bimbit mempunyai Pergerakan garis seragam MRU (kelajuannya tetap).

Secara umum, fungsi V (t) Ia juga merupakan fungsi masa, yang seterusnya dapat diperoleh. Bagaimana jika tidak mungkin untuk mencari yang diperoleh dari fungsi x (t) dan V (t)?

Dalam kes x (t) Mungkin bahawa cerun - kelajuan seketika - tanda berubah dengan ketara. Atau yang akan lulus dari sifar ke nilai yang berbeza dengan segera.

Jika ya grafik x (t) Ia akan membentangkan petua atau sudut pada perubahan secara tiba -tiba. Sangat berbeza dari kes yang diwakili dalam imej sebelumnya, di mana lengkungnya x (t) Ia adalah lengkung lembut, tanpa titik, sudut, ketidakselarasan atau perubahan mendadak.

Boleh melayani anda: Bose Einstein Condensate

Kebenarannya ialah untuk telefon bimbit sebenar, lengkung lembut adalah yang terbaik mewakili tingkah laku objek.

Pergerakan umum agak rumit. Mudah alih boleh dihentikan untuk seketika, mempercepatkan untuk bergerak dari rehat untuk mendapatkan kelajuan dan menjauhkan diri dari titik permulaan, teruskan kelajuan untuk seketika, kemudian berhenti untuk berhenti lagi dan dengan itu gaya.

Mereka boleh bermula semula dan terus ke arah yang sama. Atau bertindak kemunduran dan kembali. Ini dipanggil pergerakan yang bervariasi dalam dimensi.

Di bawah beberapa contoh pengiraan kelajuan serta -merta akan menjelaskan penggunaan definisi yang diberikan:

Diselesaikan latihan kelajuan serta -merta

Latihan 1

Zarah bergerak sepanjang garis lurus dengan undang -undang pergerakan berikut:

x (t) = -t³ + 2 t² + 6 T - 10

Semua unit berada dalam sistem antarabangsa. Cari:

a) Kedudukan zarah pada t = 3 saat.

b) Kelajuan purata dalam selang antara t = 0 s dan t = 3 s.

c) kelajuan purata dalam selang antara t = 0 s dan t = 3 s.

d) Kelajuan seketika zarah soalan sebelumnya, pada t = 1 s.

Jawapan

a) Untuk mencari kedudukan zarah, undang -undang pergerakan (fungsi kedudukan) pada t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Tidak ada masalah bahawa kedudukannya negatif. Tanda (-) menunjukkan bahawa zarah berada di sebelah kiri asal atau.

b) Dalam pengiraan kelajuan purata, kedudukan akhir dan awal zarah diperlukan pada masa yang ditunjukkan: x (3) dan x (0). Kedudukan pada t = 3 adalah x (3) dan diketahui mengenai hasil sebelumnya. Kedudukan pada t = 0 saat ialah x (0) = -10 m.

Boleh melayani anda: statik: sejarah, kajian apa, aplikasi, undang -undang

Oleh kerana kedudukan akhir adalah sama dengan yang awal, ia segera menyimpulkan bahawa kelajuan purata adalah 0.

c) kelajuan purata adalah sebab antara jarak perjalanan dan masa yang dihabiskan. Sekarang, jarak adalah modul atau magnitud anjakan, oleh itu:

Jarak = | x2 - x1 | = | -10-(-10) | M = 20 m

Perhatikan bahawa jarak perjalanan sentiasa positif.

v_{M = 20 m/3 s = 6.7 m/s}

d) Di sini adalah perlu untuk mencari derivatif pertama kedudukan mengenai masa. Kemudian ia dinilai untuk t = 1 saat.

x '(t) = -4 t² + 4 T + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Latihan 2

Berikut adalah graf kedudukan mudah alih sebagai fungsi masa. Cari kelajuan seketika pada t = 2 saat.

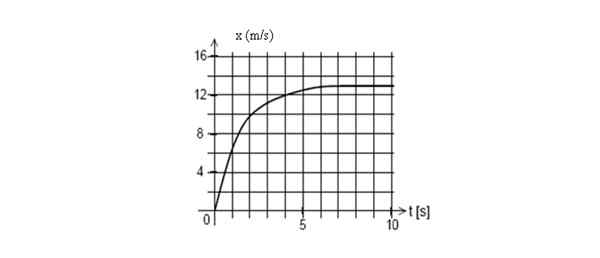Graf kedudukan berbanding masa untuk telefon bimbit. Sumber: Diri Diri.

Jawapan

Lukis garis tangen ke lengkung pada t = 2 saat, kemudian hitung cerun anda, mengambil dua titik garis.

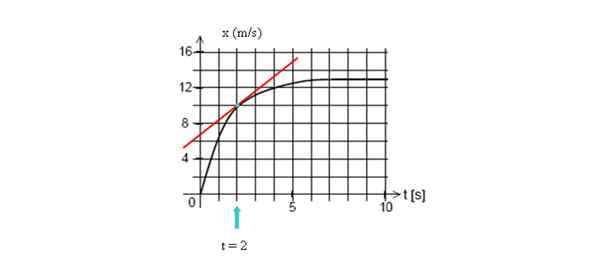Untuk mengira kelajuan seketika pada titik yang ditunjukkan, lukis garis tangen ke titik itu dan cari cerunnya. Sumber: Diri Diri.

Dalam contoh ini kita akan mengambil dua mata yang mudah digambarkan, yang koordinatnya (2 s, 10 m) dan potong dengan paksi menegak (0 s, 7 m):

Rujukan

1. Giancoli, d. Fizik. Prinsip dengan aplikasi. 6^th Edisi. Prentice Hall. 22-25.
2. Resnick, r. (1999). Fizikal. Jilid 1. Edisi ketiga dalam bahasa Sepanyol. Mexico. Syarikat Editorial Continental s.Ke. daripada c.V. 21-22.
3. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. 7^ma. Edisi. Mexico. Editor Pembelajaran Cengage. 23-25.