Konsep konsep percuma, persamaan, latihan diselesaikan

The jatuh bebas Ia adalah pergerakan menegak yang mengalami objek apabila ia jatuh dari ketinggian tertentu berhampiran permukaan bumi. Ia adalah salah satu pergerakan paling mudah dan paling segera yang diketahui: dalam garis lurus dan dengan pecutan berterusan.

Semua objek yang dijatuhkan, atau yang dilemparkan secara menegak ke atas atau ke bawah, bergerak dengan pecutan 9.8 m/s² disediakan oleh keterukan bumi, tanpa mengira jisimnya.

Kejatuhan percuma dari tebing. Sumber: Pexels.com.

Fakta ini boleh diterima hari ini tanpa masalah. Walau bagaimanapun, memahami sifat sebenar kejatuhan bebas mengambil sedikit masa. Orang Yunani telah menerangkannya dan ditafsirkan pada dasarnya pada abad keempat a c.

[TOC]

Persamaan pergerakan jatuh bebas

Setelah yakin bahawa percepatan adalah sama untuk semua badan yang dikeluarkan di bawah tindakan graviti, sudah tiba masanya untuk menubuhkan persamaan yang diperlukan untuk menjelaskan pergerakan ini.

Penting untuk menekankan bahawa rintangan udara tidak diambil kira dalam model pergerakan pertama ini. Walau bagaimanapun, hasil model ini sangat tepat dan dekat dengan realiti.

Dalam semua perkara yang berikut, model zarah akan dianggap, iaitu, dimensi objek tidak diambil kira, dengan mengandaikan bahawa keseluruhan jisim tertumpu dalam satu titik.

Untuk pergerakan rectilinear yang dipercepatkan secara seragam, ia diambil sebagai paksi rujukan ke paksi dan. Pengertian positif diambil dan negatif turun.

Magnitud kinematik

Dengan cara ini, persamaan kedudukan, kelajuan dan pecutan bergantung pada masa:

Pecutan

A = g = -9.8 m/s² (-32 kaki/s²)

Kedudukan bergantung pada masa: dan (t)

y = y_{Sama ada} + v_{Sama ada} . T + ½ gt²

Di mana dan_{Sama ada} Ia adalah kedudukan awal mudah alih dan v_{Sama ada} adalah kelajuan awal. Ingat bahawa dalam pelancaran menegak sehingga halaju awal semestinya berbeza dari 0.

Yang boleh ditulis sebagai:

dan - dan_{Sama ada} = v_{Sama ada} . T + ½ gt²

Δy = v_{Sama ada} . T + ½ gt²

Dengan δdan Menjadi anjakan yang dibuat oleh zarah mudah alih. Dalam unit sistem antarabangsa kedua -dua kedudukan dan anjakan diberikan dalam meter (m).

Kelajuan bergantung pada masa: V (t)

V = V_{Sama ada} + g . t

Kelajuan bergantung pada anjakan

Adalah mungkin untuk menyimpulkan persamaan yang menghubungkan anjakan dengan kelajuan, tanpa masa campur tangan. Untuk melakukan ini, masa persamaan terakhir dibersihkan:

Boleh melayani anda: Model mekanikal kuantum atom

 Dan ia digantikan dalam persamaan anjakan:

Δy = v_{Sama ada} . T + ½ gt²

The Square dibangunkan dengan bantuan produk dan istilah yang luar biasa dikumpulkan semula.

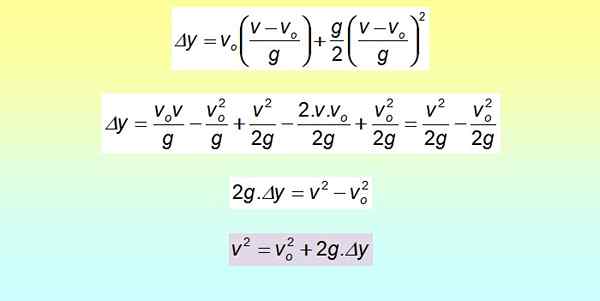
Persamaan ini berguna apabila masa tidak tersedia, tetapi sebaliknya terdapat kelajuan dan anjakan, seperti yang akan dilihat di bahagian contoh yang diselesaikan.

Contoh kejatuhan percuma

Pembaca yang penuh perhatian akan melihat kehadiran halaju awal v_{Sama ada}. Persamaan sebelumnya sah untuk pergerakan menegak di bawah tindakan graviti, kedua -dua objek jatuh dari ketinggian tertentu, seolah -olah ia dibuang secara menegak ke atas atau ke bawah.

Apabila objek jatuh, ia hanya dilakukan v_{Sama ada} = 0 dan persamaan dipermudahkan seperti berikut.

Pecutan

A = g = -9.8 m/s² (-32 kaki/s²)

Kedudukan bergantung pada masa: dan (t)

y = y_{Sama ada}+ ½ gt²

Kelajuan bergantung pada masa: V (t)

v = g . t

Kelajuan bergantung pada anjakan

v² = 2g. Dy

Dy Ia juga akan negatif, sejak v² Ia mesti jumlah positif. Ini akan berlaku sekiranya asal Sama ada sifar sistem koordinat di titik pelancaran atau di tanah.

Sekiranya pembaca lebih suka, ia boleh mengambil arah ke bawah sebagai positif. Graviti akan terus bertindak jika difikirkannya + 9.8 m/s². Tetapi anda mesti selaras dengan konvensyen tanda yang dipilih.

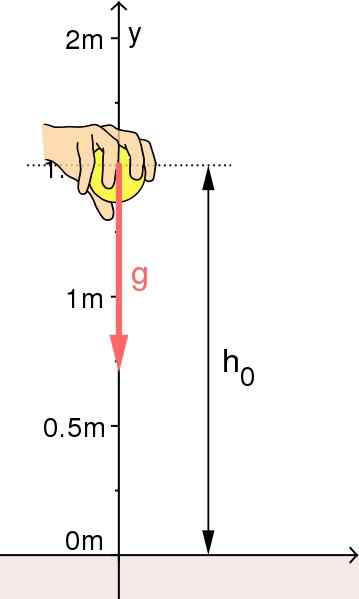Kejatuhan Objek Percuma: Asal sistem rujukan telah dipilih di tanah. Sumber: Sumber: Mikerun [CC BY-SA 4.0 (https: // creativeCommons.Org/lesen/by-sa/4.0)]

Pelancaran menegak

Di sini, secara semulajadi, kelajuan awal tidak boleh dibatalkan. Kita mesti memberikan objek untuk dorongan untuk naik. Menurut kelajuan awal yang disediakan, objek akan meningkat ke ketinggian yang lebih besar atau lebih rendah.

Sudah tentu, akan ada momen di mana objek itu berhenti seketika. Maka ketinggian maksimum akan dicapai berkenaan dengan titik pelancaran. Juga pecutan masih g ke bawah. Mari lihat apa yang berlaku dalam kes ini.

Pengiraan ketinggian maksimum yang dicapai

Memilih saya = 0:

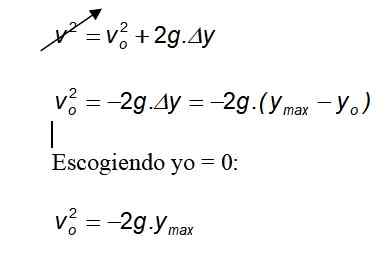
Oleh kerana graviti selalu menunjuk ke tanah ke arah negatif, tanda negatif dibatalkan.

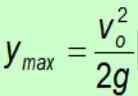
Pengiraan masa maksimum

Prosedur yang sama berfungsi untuk mencari masa yang diperlukan untuk objek mencapai ketinggian maksimum.

V = V_{Sama ada} + g . t

Ia tidak V = 0

v_{Sama ada} = - g . t_Maks

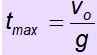
Masa penerbangan adalah masa objek yang berlangsung di udara. Sekiranya objek kembali ke titik permulaan, masa kenaikan adalah sama dengan masa keturunan. Oleh itu, masa penerbangan adalah 2. T max.

Boleh melayani anda: Skala mikroskopik: sifat, kiraan zarah, contoh

Adalah dua kali t_Maks Jumlah masa objek berlangsung di udara? Ya, selagi objek bermula dari satu titik dan kembali ke sana.

Sekiranya pelancaran dibuat dari ketinggian tertentu di atas tanah dan objek dibenarkan untuk meneruskannya, masa penerbangan tidak lagi menjadi dua kali ganda masa maksimum.

Latihan yang diselesaikan

Dalam resolusi latihan yang berikut, berikut akan dipertimbangkan:

1-ketinggian dari mana objek dijatuhkan adalah kecil berbanding jejari bumi.

2-rintangan udara hina.

3-Nilai pecutan graviti adalah 9.8 m/s²

4-Apabila ia adalah masalah dengan mudah alih tunggal, lebih baik dipilih dan_{Sama ada} = 0 pada titik permulaan. Ini biasanya memudahkan pengiraan.

5-Pada kurang daripada sebaliknya ditunjukkan, arah ke atas diambil sebagai positif.

6 -Dalam pergerakan gabungan yang menaik dan menurun, persamaan yang digunakan secara langsung menawarkan hasil yang betul, selagi konsistensi dikekalkan dengan tanda -tanda: naik positif, ke bawah negatif dan keterukan -9.8 m/s² atau -10 m/s² Sekiranya anda lebih suka bulat (untuk lebih selesa apabila mengira).

Latihan 1

Bola dilemparkan secara menegak dengan kelajuan 25.0 m/s. Jawab soalan berikut:

a) berapa banyak ia meningkat?

b) Berapa lama masa yang diperlukan untuk mencapai titik tertinggi?

c) Berapa lama bola mengambil untuk menyentuh permukaan bumi setelah mencapai titik tertinggi?

d) Apakah kelajuan anda apabila anda kembali ke tahap di mana ia bermula?

Penyelesaian

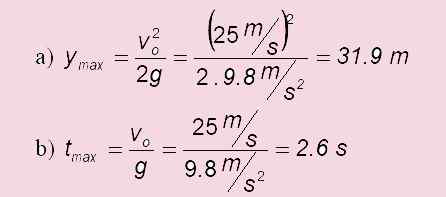
c) Dalam kes pelancaran tahap: t_penerbangan = 2 . t_Maks = 2 x6 s = 5.1 s

d) Apabila ia kembali ke titik permulaan, kelajuan mempunyai magnitud yang sama dengan kelajuan awal tetapi arah yang bertentangan, oleh itu ia mesti - 25 m/s. Ia mudah diperiksa dengan menggantikan nilai dalam persamaan untuk kelajuan:

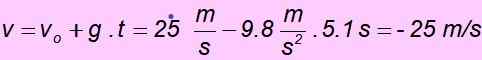
Latihan 2

Beg pakaian pos kecil dibebaskan dari helikopter yang turun dengan kelajuan tetap 1.50 m/s. Selepas 2.00 s mengira:

a) Berapakah kelajuan beg itu?

b) sejauh mana beg pakaian di bawah helikopter?

c) Apakah jawapan anda untuk bahagian a) dan b) jika helikopter meningkat dengan kelajuan berterusan 1.50 m/s?

Penyelesaian

Bahagian a

Ketika meninggalkan helikopter, beg itu membawa kelajuan awalnya v_{Sama ada} = -1.50 m/s. Dengan masa yang dinyatakan, kelajuan telah meningkat terima kasih kepada pecutan graviti:

Boleh melayani anda: badan angkasa

V = V_{Sama ada} + g . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Bahagian b

Mari kita lihat berapa banyak beg itu turun berkenaan dengan titik permulaan pada masa itu:

Beg pakaian: Dy = v_{Sama ada} . T + ½ gt² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Ia telah dipilih dan_{Sama ada} = 0 Di titik permulaan, seperti yang ditunjukkan pada permulaan bahagian. Tanda negatif menunjukkan bahawa beg itu turun 22. 6 m di bawah titik permulaan.

Sementara itu helikopter Ia telah jatuh cepat -1.50 m/s, kami mengandaikan secara berterusan, oleh itu dalam masa yang ditunjukkan selama 2 saat, helikopter telah mengembara:

Helikopter: δy = v_{Sama ada}.t = -1.lima puluh x 2 m = -3 m.

Oleh itu selepas 2 saat, beg pakaian dan helikopter dipisahkan dengan jarak dari:

D =| -22.6 - (-3) | M = 19. 6 m.

Jarak selalu positif. Untuk menyerlahkan fakta ini, nilai mutlak digunakan.

Bahagian c

Apabila helikopter meningkat, ia mempunyai kelajuan + 1.5 m/s. Dengan kelajuan beg itu keluar, sehingga selepas 2 s sudah membawa:

V = V_{Sama ada} + g . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

Kelajuan ternyata negatif, kerana selepas 2 saat beg itu bergerak ke bawah. Telah meningkat terima kasih kepada graviti, tetapi tidak seperti dalam Bahagian A.

Sekarang kita akan dapati berapa banyak beg itu telah turun berkenaan dengan titik permulaan semasa perjalanan 2 saat pertama:

Valija: δy = v_{Sama ada} . T + ½ gt² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Sementara itu, helikopter Ia telah meningkat Mengenai titik permulaan, dan telah melakukannya dengan kelajuan yang berterusan:

Helikopter: δy = v_{Sama ada}.T = +1.lima puluh x 2 m = +3 m.

Selepas 2 saat beg dan helikopter dipisahkan dengan jarak dari:

D =| -16.6 - (+3) | M = 19.6 m

Jarak yang memisahkannya adalah sama dalam kedua -dua kes. Koper itu bergerak kurang jarak menegak dalam kes kedua, kerana kelajuan awalnya diarahkan ke atas.

https: // youuat.BE/W2UVETXWSFK

Rujukan

1. Kirkpatrick, l. 2007. Fizik: Lihatlah dunia. 6^TA Edisi Singkat. Pembelajaran Cengage.  23 - 27.
2. Rex, a. 2011. Asas Fizik. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. 14^th. Ed. Jilid1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Asas Fizik. 9^na Ed. Pembelajaran Cengage. 43 - 55.
5. Wilson, J. 2011. Fizik 10. Pendidikan Pearson. 133 - 149.