Beban Radial Bagaimana latihan yang dikira, diselesaikan

The Beban radial Ia adalah kekuatan yang dilaksanakan secara serentak ke paksi simetri objek dan garis tindakannya melalui paksi ini. Contohnya, tali pinggang pada takal mengenakan beban radial pada galas atau galas paksi yang sama.

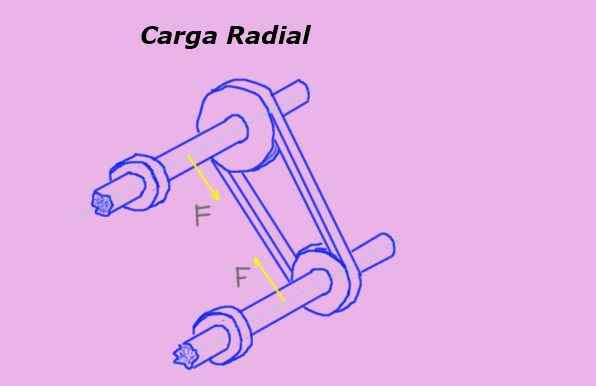
Dalam Rajah 1 anak panah kuning mewakili daya radial pada paksi kerana ketegangan tali pinggang yang melewati kendi.

Rajah 1. Beban radial pada paksi pulley. Sumber: Diri Diri.

Unit ukuran beban radial dalam sistem antarabangsa atau jika ia adalah Newton (n). Tetapi unit kuasa lain juga digunakan untuk mengukurnya, seperti kuasa kilogram (kg-f) dan kekuatan paun (LB-F).

[TOC]

Bagaimana ia dikira? 

Untuk mengira nilai beban radial dalam unsur -unsur struktur, langkah -langkah berikut mesti diikuti:

- Buat gambarajah daya pada setiap elemen.

- Memohon persamaan yang menjamin keseimbangan translasi; iaitu, jumlah semua kuasa adalah batal.

- Pertimbangkan persamaan tork atau momen supaya keseimbangan putaran dipenuhi. Dalam kes ini jumlah semua tork mesti dibatalkan.

- Kirakan daya untuk mengenal pasti beban radial yang bertindak dalam setiap elemen.

Latihan yang diselesaikan

-Latihan 1

Angka berikut menunjukkan takal di mana pulley tegang berlalu dengan ketegangan t. Pulley dipasang pada paksi yang terletak pada dua chumaceras. Pusat salah seorang daripada mereka berada di jarak l₁ dari pusat takal. Di hujung yang lain adalah chumacera yang lain, pada jarak l₂.

Boleh melayani anda: higroscopicity: konsep, bahan hygroscopic, contoh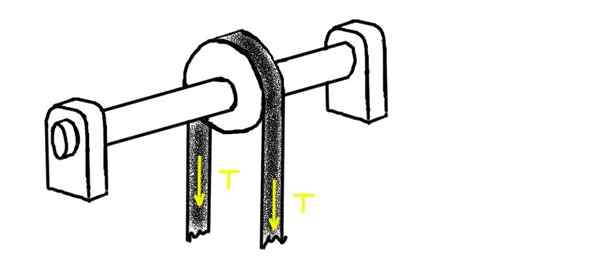Rajah 2. Pulley di mana tali tegang berlalu. Sumber: Diri Diri.

Tentukan beban radial pada setiap chumaceras, dengan mengandaikan bahawa berat paksi dan takalnya agak lebih rendah daripada voltan yang digunakan.

Ambil nilai untuk voltan tali 100 kg-f dan untuk jarak l₁= 1 m dan l₂= 2 m.

Penyelesaian

Di tempat pertama, gambarajah daya yang bertindak pada paksi dibuat.

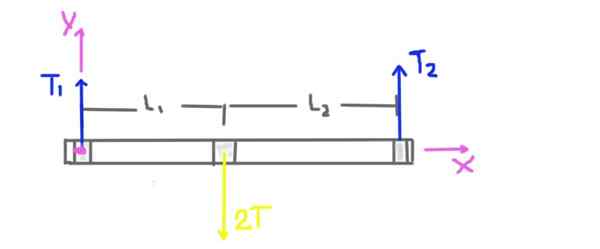Rajah 3. Gambar Rajah Latihan 1.

Voltan pulley adalah t, tetapi beban radial pada paksi dalam kedudukan pulley adalah 2T. Berat paksi dan takal tidak diambil kira kerana pernyataan masalah memberitahu kita bahawa ia jauh lebih rendah daripada voltan yang digunakan pada tali pinggang.

Reaksi radial sokongan sokongan disebabkan oleh daya radial atau beban T1 dan T2. Jarak L1 dan L2 sokongan ke pusat pulley juga ditunjukkan dalam rajah.

Sistem koordinat juga ditunjukkan. Tork atau momen total pada paksi akan dikira mengambil sebagai pusat asal sistem koordinat dan akan positif ke arah z.

Keadaan keseimbangan

Keadaan keseimbangan kini ditubuhkan: jumlah sifar dan jumlah tork yang sama sama dengan sifar.

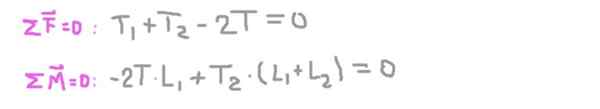
Dari persamaan kedua reaksi radial pada paksi pada sokongan 2 (t₂), menggantikan yang pertama dan membersihkan reaksi radial pada paksi dalam sokongan 1 (t₁).

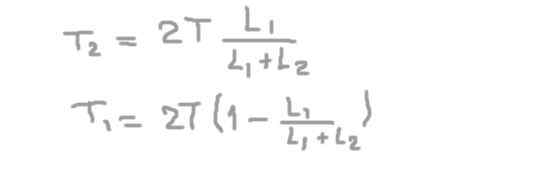Jika kita menggantikan data berangka, kita dapati bahawa beban radial atau daya pada paksi dalam kedudukan sokongan 1 adalah:

T₁= (2/3) t = 66.6 kg-f

Ia boleh melayani anda: lengkung penentukuran: Apa itu, bagaimana untuk melakukannya, contohnya

Dan beban radial pada paksi dalam sokongan sokongan 2 adalah:

T₂= (4/3) t = 133.3 kg-f.

Latihan 2

Angka berikut menunjukkan sistem yang terdiri daripada tiga pulley a, b, c semua radio r. Kendi dihubungkan dengan tali pinggang yang mempunyai voltan T.

Paksi a, b, c lulus galas pelincir. Pemisahan antara pusat paksi a dan b adalah 4 kali jejari r r. Begitu juga, pemisahan antara paksi b dan c juga 4r.

Tentukan beban radial pada paksi kendi A dan B, dengan mengandaikan bahawa ketegangan tali pinggang adalah 600N.

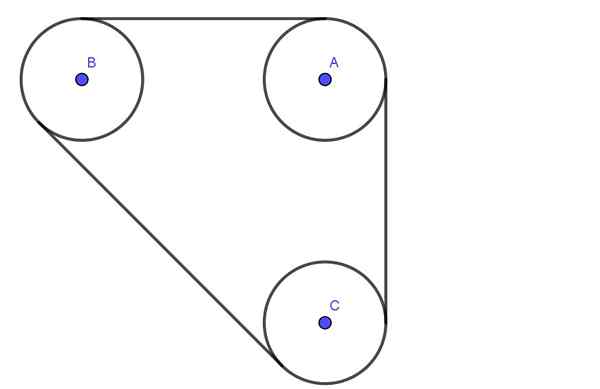Rajah 4. Sistem pulley. Latihan 2. (Huraian sendiri)

Penyelesaian

Ia bermula dengan melukis gambarajah daya yang bertindak pada pulley a dan b. Pada yang pertama anda mempunyai ketegangan kedua₁ dan t₂, serta daya f_Ke Bahawa galas itu dikenakan pada paksi takal.

Begitu juga, pada pulley b anda mempunyai ketegangan t₃ , T₄ dan daya f_B bahawa galas itu menggunakan paksi yang sama. Beban radial pada paksi pulley a adalah daya f_Ke dan beban radial pada b ialah daya f_B.

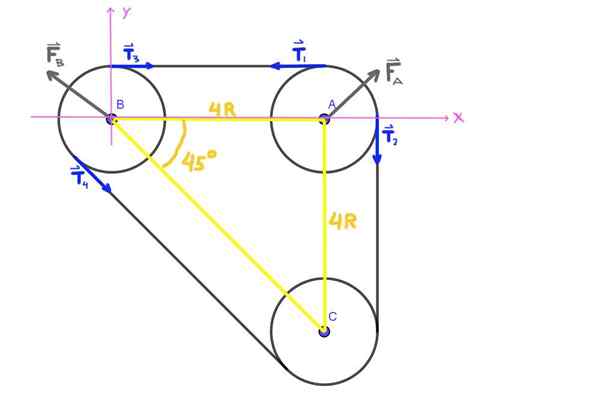Rajah 5. Gambar Rajah, Latihan 2. (Huraian sendiri)

Sebagai paksi a, b, c membentuk segitiga isorektangle, sudut ABC adalah 45 °.

Semua ketegangan t₁ , T₂ , T₃ , T₄ yang ditunjukkan dalam angka mempunyai modul yang sama, iaitu voltan tali pinggang.

Keadaan keseimbangan untuk pulley a

Sekarang kita menulis keadaan keseimbangan untuk takal yang mana ia tidak lain dari jumlah semua kekuatan yang bertindak pada takal yang mesti dibatalkan.

Memisahkan komponen x dan y dari daya dan menambah (secara vektor) pasangan persamaan skalar berikut diperoleh:

Boleh melayani anda: Titan (satelit)

F_KeX - T = 0; F_KeDan - T = 0

Persamaan ini membawa kepada kesamaan berikut: f_Kapak = F_Oh = T.

Oleh itu beban radial mempunyai magnitud yang diberikan oleh:

F_Ke = (T² + t²)^1/2 = 2^1/2∙ t = 1.41 ∙ t = 848.5 n. Arah 45 °. 

Keadaan keseimbangan untuk pulley b

Begitu juga, kita menulis keadaan keseimbangan untuk pulley b. Untuk komponen x yang anda ada: f_BX + T + t ∙ cos45 ° = 0

Dan untuk komponen y: f_BDan + T ∙ sen45 ° = 0

Oleh itu:

F_Bx = - t (1+2^-1/2) dan f_Oleh = -T ∙ 2^-1/2

Iaitu, magnitud beban radial pada pulley b ialah:

F_B = ((1+2^-1/2) ² + 2^-1)^1/2∙ t = 1.85 ∙ t = 1108.66 n dan alamatnya adalah 135 °.

Rujukan

1. Beer F, Johnston E, Dewolf J, Mazurek, D. Bahan mekanik. Edisi Kelima. 2010. MC Graw Hill. 1-130.
2. Gere J, Goodno, B. Bahan mekanik. Edisi Kelapan. Pembelajaran Cengage. 4-220.
3. Giancoli, d. 2006. Fizik: Prinsip dengan aplikasi. 6^Tth Ed. Prentice Hall. 238-242.
4. Hibbeler R. Bahan mekanik. Edisi Kelapan. Prentice Hall. 2011. 3-60.
5. Valera Negrete, J. 2005. Nota Fizik Umum. Unam. 87-98.