Formula koefisien korelasi, pengiraan, tafsiran, contoh

Dia Koefisien korelasi Dalam statistik ia adalah penunjuk yang mengukur trend dua pembolehubah kuantitatif x dan y untuk mempunyai hubungan linearity atau proporsionality antara mereka.

Umumnya, pasangan pembolehubah x dan y adalah dua ciri populasi yang sama. Sebagai contoh, x boleh menjadi ketinggian seseorang dan berat badannya.

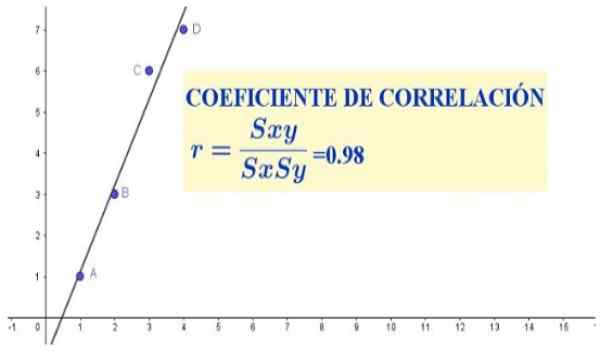
Rajah 1. Koefisien korelasi untuk empat pasangan data (x, y). Sumber: f. Zapata.

Dalam kes ini, pekali korelasi akan menunjukkan sama ada atau tidak terdapat nisbah perkadaran antara ketinggian dan berat populasi tertentu.

Koefisien korelasi linear Pearson dilambangkan dengan surat itu r huruf kecil dan nilai minimum dan maksimum masing -masing adalah -1 dan +1. 

Nilai r = +1 akan menunjukkan bahawa seluruh pasangan (x, y) sejajar dengan sempurna dan apabila x tumbuh, dan akan tumbuh dalam bahagian yang sama. Sebaliknya, jika ia berlaku bahawa r = -1, set pasangan juga akan sejajar dengan sempurna, tetapi dalam hal ini ketika x tumbuh, dan berkurangan dalam perkadaran yang sama.

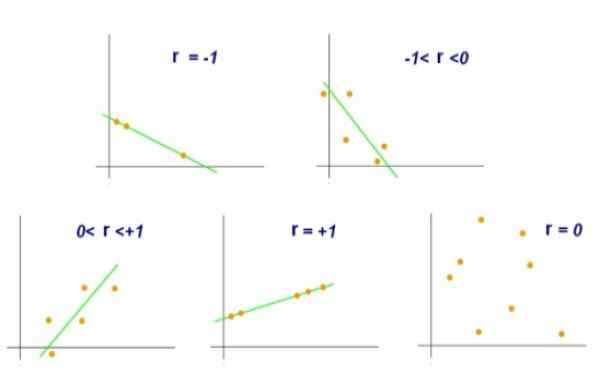Rajah 2. Nilai yang berbeza dari pekali korelasi linear. Sumber: Wikimedia Commons.

Sebaliknya, nilai r = 0 akan menunjukkan bahawa tiada korelasi linear antara pembolehubah x dan y. Walaupun nilai r = +0.8 akan menunjukkan bahawa pasangan (x, y) cenderung untuk berkumpul ke satu sisi dan satu lagi garis tertentu.

Formula untuk mengira pekali korelasi r adalah seperti berikut:

Di mana pengangka mewakili kovarians antara pembolehubah x dan y, manakala penyebut adalah hasil sisihan piawai untuk pembolehubah x dan sisihan piawai untuk pembolehubah dan.

Cara mengira pekali korelasi?

Koefisien korelasi linear adalah jumlah statistik yang dimasukkan ke dalam kalkulator saintifik, dalam kebanyakan spreadsheet dan program statistik.

Boleh melayani anda: Paraboloid hiperbolik: Definisi, sifat dan contoh

Walau bagaimanapun, adalah mudah untuk mengetahui bagaimana formula yang mentakrifkannya digunakan, dan untuk ini pengiraan terperinci akan dipaparkan, dijalankan pada set data kecil.

Dan seperti yang dinyatakan dalam bahagian sebelumnya, pekali korelasi adalah kovarians SXY yang dibahagikan dengan produk sisihan piawai SX untuk pembolehubah x dan sy untuk pembolehubah dan.

Kovarians dan varians

Kovarians SXY adalah:

Sxy = [σ (xi -) (yi -)] / (n -1)

Di mana jumlahnya dari 1 hingga pasangan n (xi, yi). E adalah stoking aritmetik data xi e yi masing -masing.

Bagi bahagiannya, sisihan piawai untuk pembolehubah x adalah akar kuadrat dari varians set data xi, dengan i dari 1 hingga n:

Sx = √ [σ (xi -)^2) / (n -1)]

Begitu juga, sisihan piawai untuk pembolehubah dan merupakan akar kuadrat dari varians set data Yi, dengan i dari 1 hingga n:

Sy = √ [σ (yi -)² ) / (N-1)]

Kes ilustrasi

Untuk menunjukkan secara terperinci cara untuk mengira pekali korelasi, kami akan mengambil set berikut empat pasang data 

(X, y): (1, 1); (23); (3, 6) dan (4, 7).

Mula -mula kita mengira min aritmetik untuk x dan y, seperti berikut:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Kemudian parameter yang tinggal dikira:

SXY Covariance

Sxy = [(1 - 2.5) (1 - 4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. .… .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Boleh melayani anda: peraturan derivasi (dengan contoh)

… .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Sisihan piawai SX

Sx = √ [(-1.5)² + (-0.5)² + (0.5)² + (1.5)²) / (4-1)] = √ [5/3] = 1.29

Sisihan piawai sy

Sx = √ [(-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (4-1)] = 

√ [22.75/3] = 2.75

Pekali pagar r

R = 3.5 / (1.29 * 2.75) = 0.98

Tafsiran

Dalam set data kes sebelumnya terdapat korelasi linear yang kuat antara pembolehubah x dan y, yang menunjukkan kedua -dua graf penyebaran (yang dapat dilihat dalam Rajah 1) dan dalam pekali korelasi, yang melemparkan nilai yang agak dekat dengan Unit tersebut.

Setakat pekali korelasi lebih dekat dengan 1 atau -1, lebih masuk akal menjadikan penetapan data ke garisan, hasil regresi linear.

Regresi linear

Garis regresi linear diperoleh dari Kaedah sekurang -kurangnya dataran. di mana parameter garis regresi diperolehi daripada pengurangan jumlah kuadrat perbezaan antara nilai dan dianggarkan dan yi data n.

Sebaliknya, parameter a dan b garis regresi y = a + bx, yang diperolehi oleh kaedah dataran minimum, adalah:

*B = sxy / (sx²) Untuk cerun

*A = - b untuk persimpangan garis regresi dengan paksi dan.

Ingatlah bahawa SXY adalah kovarians yang ditakrifkan di atas dan SX² Ia adalah varians atau kuadrat sisihan piawai yang ditakrifkan sebelumnya. E adalah cara aritmetik data x dan dan masing -masing.

Contoh

Koefisien korelasi digunakan untuk menentukan sama ada terdapat korelasi jenis linear antara dua pembolehubah. Ia boleh digunakan apabila pembolehubah yang dikaji adalah kuantitatif dan juga, mereka sepatutnya mengikuti taburan jenis biasa.

Dapat melayani anda: peraturan korespondensi fungsi

Contoh ilustrasi yang kita ada di bawah: ukuran tahap obesiti adalah indeks jisim badan, yang diperolehi dengan membahagikan berat satu orang ke kilogram antara ketinggian yang sama di unit persegi ke dataran.

Diinginkan untuk mengetahui sama ada terdapat korelasi yang kuat antara indeks jisim badan dan kepekatan kolesterol HDL dalam darah, diukur dalam milimol seliter. Untuk tujuan ini, kajian telah dilakukan dengan 533 orang yang diringkaskan dalam graf berikut, di mana setiap titik mewakili data seseorang.

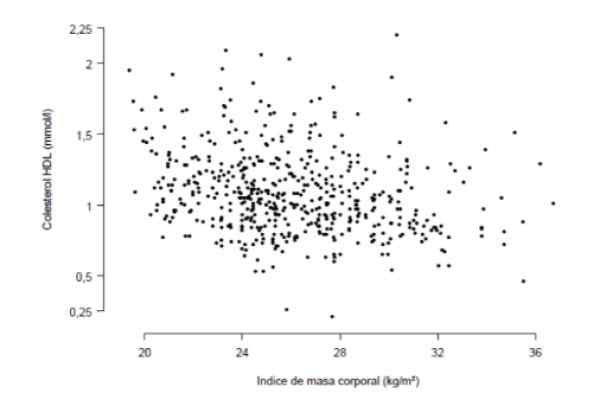Rajah 3. Kajian IMC dan Kolesterol HDL di 533 pesakit. Sumber: Institut Sains Kesihatan Aragonese (IACs).

Dari pemerhatian yang teliti terhadap graf, ia mengikuti bahawa terdapat trend linear (tidak terlalu jelas) antara kepekatan kolesterol HDL dan indeks jisim badan. Ukuran kuantitatif trend ini adalah pekali korelasi yang untuk kes ini ternyata r = -0,276.

Rujukan

1. González c. Statistik Umum. Pulih dari: tarwi.La Molina.Edu.PE
2. IACS. Institut Sains Kesihatan Aragonese. Diperolehi dari: ICS-Aragon.com 
3. Salazar c. dan Castillo s. Prinsip Statistik Asas. (2018). Diperolehi dari: DSPACE.Uce.Edu.Ec
4. Superprof. Koefisien korelasi. Pulih dari: superprof.adalah
5. USAC. Manual Statistik Deskriptif. (2011). Pulih dari: statistik.kejuruteraan.USAC.Edu.Gt
6. Wikipedia. Koefisien korelasi Pearson. Pulih dari: Adakah.Wikipedia.com.