Fizikal

Boltzmann Sejarah, Persamaan, Pengiraan, Latihan Boltzmann

Boltzmann Sejarah, Persamaan, Pengiraan, Latihan Boltzmann

The Boltzmann Constant Ia adalah nilai yang mengaitkan purata tenaga kinetik sistem termodinamik atau objek dengan suhu mutlak yang sama. Walaupun mereka sering keliru, suhu dan tenaga bukan konsep yang sama.

Suhu adalah ukuran tenaga, tetapi bukan tenaga itu sendiri. Dengan pemalar Boltzmann, satu dikaitkan antara satu sama lain seperti berikut:

Danc = (3/2) kB  T

Tuan rumah Boltzmann di Vienna. Sumber: Dadotet di Bahasa Inggeris Wikipedia [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/]]

Persamaan ini sah untuk molekul gas monoatomik yang ideal m, di mana Danc Ia adalah tenaga kinetiknya yang diberikan dalam joules, kB Ia adalah pemalar Boltzmann dan T Ia adalah suhu mutlak di kelvin.

Dengan cara ini, apabila suhu meningkat, purata tenaga kinetik oleh molekul bahan juga meningkat, seperti yang dijangkakan akan berlaku. Dan sebaliknya berlaku apabila suhu berkurangan, dapat mencapai titik di mana pergerakan keseluruhan terhenti, suhu terendah atau suhu mutlak dicapai.

Semasa bercakap mengenai tenaga kinetik purata, perlu diingat bahawa tenaga kinetik dikaitkan dengan pergerakan. Dan zarah dapat bergerak dalam banyak cara, contohnya bergerak, berputar atau bergetar. Sudah tentu, tidak semua akan melakukannya dengan cara yang sama, dan kerana ia tidak terhingga, maka purata diambil untuk mencirikan sistem.

Beberapa keadaan tenaga lebih cenderung daripada yang lain. Konsep ini sangat penting dalam termodinamik. Tenaga yang dipertimbangkan dalam persamaan sebelumnya adalah tenaga kinetik terjemahan. Kebarangkalian negeri dan hubungan mereka dengan pemalar Boltzmann akan bercakap sedikit kemudian.

Pada tahun 2018, Kelvin telah ditakrifkan semula dan bersamanya Boltzmann Constant, yang dalam sistem antarabangsa adalah kira -kira 1.380649 x 10-23 J. K-1. Lebih banyak ketepatan dapat dicapai untuk pemalar Boltzmann, yang telah ditentukan di banyak makmal di seluruh dunia, dengan kaedah yang berbeza.

[TOC]

Sejarah

Pemalar yang terkenal berhutang namanya kepada ahli fizik Ludwig Boltzmann (1844-1906), yang dilahirkan di Vienna, yang mendedikasikan hidupnya sebagai saintis untuk mengkaji tingkah laku statistik sistem dengan banyak zarah, dari sudut pandang mekanik Newtonian.

Walaupun hari ini kewujudan atom diterima secara universal, pada abad kesembilan belas kepercayaan tentang sama ada atom itu benar -benar wujud atau merupakan artifak yang banyak fenomena fizikal dijelaskan adalah dalam perdebatan penuh.

Boleh melayani anda: vektor biasa: pengiraan dan contoh

Boltzmann adalah pembela kuat kewujudan atom, dan pada waktunya dia menghadapi kritikan keras terhadap karyanya oleh banyak rakan sekerja, yang menganggap bahawa mereka mengandungi paradoks yang tidak larut.

Beliau mengisytiharkan bahawa fenomena yang dapat dilihat pada tahap makroskopik dapat dijelaskan melalui sifat statistik zarah konstituen seperti atom dan molekul.

Kritikan ini mungkin disebabkan oleh episod kemurungan yang mendalam yang menyebabkan dia mengambil nyawa sendiri pada awal bulan September 1906, ketika ia masih banyak yang perlu dilakukan, kerana dia dianggap sebagai salah satu ahli fizik teoritis yang hebat pada waktunya dan di sana sedikit kepada saintis lain yang akan menyumbang untuk menyokong kebenaran teori mereka.

Ia tidak berlaku lama selepas kematiannya apabila penemuan baru mengenai sifat atom dan zarah -zarah konstituennya akan ditambah untuk memberi alasan kepada Boltzmann.

Kerja -kerja berterusan dan Planck Boltzmann

Sekarang, pemalar Boltzmann kB Ia diperkenalkan seperti yang diketahui hari ini beberapa saat selepas kerja ahli fizik Austria. Ia adalah Max Planck, dalam undang -undang pelepasan badan hitam, kerja yang dibentangkannya pada tahun 1901, yang pada masa itu memberinya nilai 1.34 x 1023 J/k.

Menjelang tahun 1933, Boltzmann telah ditambah kepada Vienna sebagai penghormatan poster plak dengan definisi entropi yang melibatkan pemalar yang terkenal: S = kB log w, persamaan yang akan dibincangkan kemudian.

Hari ini pemalar Boltzmann sangat diperlukan dalam penerapan undang -undang termodinamik, mekanik statistik dan teori maklumat, bidang yang ahli fizik ini dengan sad end adalah perintis.

Nilai dan persamaan

Gas boleh diterangkan dalam istilah makroskopik dan juga dalam istilah mikroskopik. Untuk penerangan pertama terdapat konsep seperti ketumpatan, suhu dan tekanan.

Walau bagaimanapun, perlu diingat bahawa gas terdiri daripada banyak zarah, yang mempunyai kecenderungan global untuk tingkah laku tertentu. Ia adalah trend yang diukur secara makroskopik. Salah satu cara untuk menentukan pemalar Boltzmann adalah terima kasih kepada persamaan gas ideal:

p.V = n. R. T

Di sini p Ia adalah tekanan gas, V Ia adalah kelantangannya, n Ia adalah bilangan tahi lalat yang ada, R Ia adalah pemalar gas dan T Ia adalah suhu. Dalam mol gas ideal, hubungan berikut antara produk dipenuhi p.V, dan tenaga terjemahan kinetik K Keseluruhan set adalah:

Boleh melayani anda: Model materi korpuskular

p.V = (2/3). K

Oleh itu tenaga kinetik adalah:

K = (3/2) n.R.T

Dengan membahagikan jumlah molekul yang hadir, yang akan dipanggil n, tenaga kinetik purata satu zarah diperolehi:

Danc = K /n

Danc= (3/2n) n.R.T

Dalam mol terdapat bilangan zarah nKe, Dan oleh itu jumlah zarah adalah N = nnA, tinggal:

Danc = (3/2nnKe) n.R.T

Tepatnya kota R/nKe Ia adalah pemalar Boltzmann, menunjukkan bahawa tenaga kinetik purata terjemahan zarah hanya bergantung pada suhu mutlak dan bukan magnitud lain seperti tekanan, jumlah atau jenis molekul:

Danc = (3/2) kB. T

Pemalar dan entropi Boltzmann

Gas mempunyai suhu tertentu, tetapi suhu itu boleh sesuai dengan keadaan tenaga dalaman yang berbeza. Cara menggambarkan perbezaan ini?

Pertimbangkan pelancaran 4 syiling serentak dan cara mereka boleh jatuh:

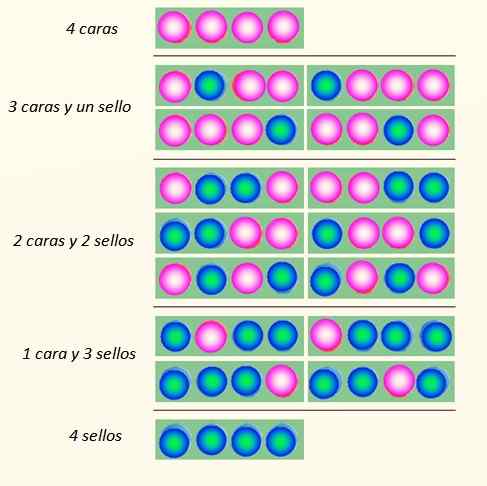Cara 4 syiling boleh jatuh. Sumber: Diri Diri

Set duit syiling boleh menganggap sejumlah 5 negeri, yang dianggap Makroskopik, diterangkan dalam angka. Yang mana di antara negeri -negeri ini akan mengatakan bahawa ia adalah yang paling mungkin?

Jawapannya mestilah keadaan 2 muka dan 2 salib, kerana ia mempunyai 6 kemungkinan, dari 16 yang digambarkan dalam angka itu. Dan 24 = 16. Ini bersamaan dengan negeri -negeri mikroskopik.

Dan bagaimana jika 20 syiling dilancarkan bukannya 4? Akan ada sejumlah 2dua puluh kemungkinan atau "keadaan mikroskopik". Ia adalah nombor yang jauh lebih besar dan lebih sukar untuk dikendalikan. Untuk memudahkan pengurusan bilangan besar, logaritma sangat sesuai.

Sekarang, apa yang kelihatannya jelas bahawa negeri dengan gangguan terbesar adalah yang paling mungkin. Negeri yang paling diperintahkan seperti 4 muka atau 4 setem sedikit berkemungkinan kecil.

Entropi keadaan makroskopik ditakrifkan sebagai:

S = kB ln w

Di mana W Ia adalah bilangan keadaan mikroskopik yang mungkin dan kB Ia adalah pemalar Boltzmann. Sebagai ln w Ia tidak berdimensi, entropi mempunyai unit yang sama seperti kB: Joule/k.

Ini adalah persamaan yang terkenal di batu nisan Boltzmann di Vienna. Walau bagaimanapun, lebih daripada entropi, yang relevan adalah perubahannya:

Ia dapat melayani anda: Pembolehubah termodinamik: yang mana dan latihan diselesaikan

ΔS = kB ln w2 - kB ln w1 = kB ln (w2/w1)

Bagaimana k dikiraB?

Nilai pemalar Boltzmann diperolehi secara eksperimen dengan pengukuran berdasarkan Thermometry akustik, yang dijalankan menggunakan harta yang menetapkan pergantungan pada kelajuan bunyi dalam gas dengan suhu yang sama.

Malah, kelajuan bunyi dalam gas diberikan oleh:

Di mana b adiabatik Ia adalah modul kebolehmampatan adiabatik yang diberikan oleh:

Badiabatik = γp

Dan ρ adalah ketumpatan gas. Untuk persamaan sebelumnya, p Ia adalah tekanan gas yang dipersoalkan dan γ Ia adalah pekali adiabatik, yang nilai untuk gas tertentu terdapat dalam jadual.

Institut Metrologi juga mengalami cara lain untuk mengukur pemalar, seperti JOHNSON HISE THERMOMETRY, yang menggunakan turun naik terma yang berlaku secara rawak dalam bahan, khususnya dalam pemandu.

Latihan yang diselesaikan

-Latihan 1

Cari:

a) Tenaga kinetik terjemahan purata Danc yang mempunyai molekul gas ideal pada 25 ºC

b) Tenaga terjemahan kinetik K molekul dalam 1 mol gas ini

c) kelajuan purata molekul oksigen pada 25 ºC

Fakta

moksigen = 16 x 10 -3 kg/mol

Penyelesaian

ke) Danc = (3/2) k t = 1.5 x 1.380649 x 10-23J. K-1 x 298 k = 6.2 x 10-dua puluh satu J

b) K = (3/2) n.R.T = 5 x 1 mol x 8.314 J/mol .K x 298 k = 3716 j

c) Danc = ½ mV2, Mengambil kira bahawa molekul oksigen adalah diatomik dan jisim molar mesti didarabkan dengan 2, ia akan menjadi:

-Latihan 2

Cari perubahan entropi apabila 1 mol gas yang diduduki dengan jumlah 0.5m3 Ia berkembang untuk menduduki 1 m3.

Penyelesaian

ΔS = kB ln (w2/w1)

W2= 2NW1 (Terdapat 24 Negeri mikroskopik untuk pelancaran 4 syiling, ingat?)

Di mana n ialah bilangan zarah yang terdapat dalam 0.5 mol gas 0.5 x nKe:

ΔS = kB ln (2N W1/w1) = kB Ln 2N= kB 0.5nKe Ln 2 = 2.88 J/k

Rujukan

  1. Atkins, ms. 1999. Kimia Fizikal. Edisi Omega. 13-47.
  2. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill. 664-672.
  3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6 ... Ed Prentice Hall. 443 -444.
  4. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1. 647-673.
  5. Jika definisi semula. Kelvin: Boltzmann Constant. Pulih dari: nist.Gov