Pecahan bersamaan dengan 2/3

The pecahan bersamaan dengan ⅔ (Dua pertiga dibaca) adalah mereka yang nilainya, dinyatakan dengan cara perpuluhan, adalah yang sama yang diperoleh dengan membahagikan 2 oleh 3: 0.6666 ... Titik Suspensive menunjukkan bahawa 6 muncul masa tak terhingga di bahagian ini.

Pecahan bersamaan dengan 2/3 adalah pecahan 4/6, kerana ternyata selepas menyelesaikan pembahagian antara 4 dan 6 secara eksplisit, perpuluhan 0.6666 .. . Maka boleh dikatakan bahawa 4/6 = 2/3 = 0.6666 .. .

Fraksi 2/3 dan 4/6 bersamaan kerana dengan membahagikan bilangan pengangka oleh penyebut angka nombor akhbar yang sama 0.66666 .. . (Sumber: f. Zapata)

Pecahan, seperti namanya, adalah sebahagian atau bahagian unit. Pecahan ⅔ diperoleh dengan membahagikan unit ke tiga bahagian yang sama dan mengambil dua bahagian tersebut.

Setiap pecahan terdiri daripada bahagian atas, yang dipanggil pengangka, dipisahkan dari bahagian bawah atau penyebut, Melalui garis pecahan. Penyebut menunjukkan berapa banyak bahagian unit dibahagikan dan pengangka menunjukkan berapa banyak pihak yang harus dipertimbangkan.

Sekarang pertimbangkan pecahan 4/6 (baca Empat keenam). Telah terbukti bahawa pecahan ini bersamaan dengan ⅔, kerana untuk membahagikan unit menjadi enam bahagian, langkah -langkah ini mesti diikuti:

1. Bahagikan unit menjadi tiga bahagian yang sama.
2. Dan kemudian membahagikan setiap bahagian ini dengan separuh, memperoleh sebanyak enam bahagian yang sama.

Sekiranya 4 bahagian 1/6 unit dikumpulkan, jumlah yang diperoleh adalah sebahagian kecil daripada nilai yang sama yang mana 2 bahagian 1/3 unit diperolehi. Dalam graf berikut, prosedur yang dijelaskan dijalankan: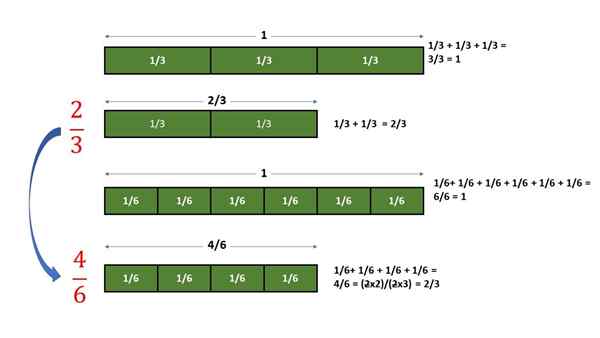

Pengesahan Grafik Bahawa Fraksi 2/3 bersamaan dengan pecahan 4/6. Sumber: f. Zapata.

Boleh melayani anda: Analogi berangka: Jenis, Aplikasi dan Latihan

Kaedah untuk mencari pecahan setara

Perhatikan bahawa pecahan setara 4/6 boleh didapati dari 2/3 dengan mengalikan oleh kedua -dua pengangka dan penyebut yang terakhir.

Apabila pada masa yang sama mengalikan pengangka dan penyebut pecahan dengan nombor yang sama, pecahan setara diperolehi.

Satu lagi cara untuk mencari pecahan yang bersamaan dengan yang lain akan membahagikan pengangka dan penyebut dengan jumlah yang sama, dengan syarat pengangka dan penyebutnya betul -betul dibahagikan dengan nombor yang sama. Tetapi tidak mungkin untuk dicapai, oleh pembahagian oleh integer yang sama, pecahan setara berdasarkan 2/3, kerana nombor 2 dan 3 adalah sepupu antara satu sama lain.

Apabila pengangka dan penyebut pecahan adalah nombor utama antara satu sama lain, dikatakan bahawa pecahannya adalah tidak dapat dipertahankan. Dan pecahan 2/3 adalah contoh yang baik dari pecahan jenis ini, sebenarnya, 2/3 mewakili set semua pecahan bersamaan dengan 0.666 ..

Sebaliknya, pecahan 4/6 boleh diturunkan dan bersamaan dengan pecahan ⅔, kerana pengangka 4 dan penyebut 6 adalah nombor, kedua -duanya boleh dibahagikan dengan 2.

Oleh itu, dua cara untuk mendapatkan pecahan bersamaan dengan yang diberikan, adalah:

• Secara serentak menguatkan pengangka dan penyebut 
• Kurangkan pengangka dan penyebut

Penguatan pecahan

Untuk mendapatkan pecahan yang bersamaan dengan yang diberikan, pengangka dan penyebutnya didarabkan dengan angka yang sama. Berikut adalah beberapa contoh:

Disimpulkan bahawa ⅔ (dua pertiga), 4/6 (empat keenam), 6/9 (enam kesembilan) dan 8/12 (lapan belas belas) adalah semua pecahan bersamaan dengan satu sama lain, tetapi daripadanya, hanya ⅔ pecahan.

Ringkasnya, jika anda bermula dari pecahan yang tidak dapat dielakkan ⅔, cara untuk mendapatkan apa -apa pecahan setara yang lain adalah untuk menggunakan formula ini:

Boleh melayani anda: Latihan pemfaktoran yang diselesaikan

Dengan integer.

Kaedah penguatan untuk mendapatkan pecahan setara. Sumber: f. Zapata

Pengurangan pecahan

Ia adalah kaedah yang membolehkan pecahan setara diperolehi, dengan syarat pecahan permulaan mempunyai pengangka dan penyebut dengan satu atau lebih pembahagi biasa.

Ia bukan kes 2/3, yang seperti yang dikatakan sebelum ini, tidak dapat dipertikaikan. Tetapi sebagai contoh, pecahan 60/90 (Enam puluh sembilan puluhan) Ia boleh dikurangkan kepada:

• 6/9, kerana kedua -dua pengangka dan penyebutnya boleh dibahagikan antara sepuluh.
• 30/45, kerana pengangka dan penyebut boleh dibahagikan antara dua.
• 20/30, kerana pengangka dan penyebut boleh dibahagikan antara tiga.
• 12/18, kerana pengangka dan penyebut boleh dibahagikan antara lima.

Sekiranya anda ingin mendapatkan pecahan yang tidak dapat dielakkan bersamaan dengan yang asal, maka perlu membahagikan kedua -dua pengangka dan penyebut oleh pembahagi maksimum (MCD).

Decomposing dalam faktor -faktor pengangka mempunyai:

60 = 2² ⋅ 3 ⋅ 5

Dan menjalankan prosedur yang sama dalam penyebut:

90 = 2 ⋅ 3² ⋅ 5

MCM adalah faktor utama biasa dengan eksponen yang lebih rendah, iaitu:

MCM (60; 90) = 233 5 = 30

Kemudian, 60 antara 30 da 2, yang diletakkan di dalam pengangka dan pada 90 antara 30 da 3, 3 diletakkan dalam penyebut. Oleh itu, pecahan 60/90 yang tidak dapat dinafikan dapat dinyatakan sebagai:

Cara untuk menentukan sama ada pecahan yang diberikan bersamaan dengan 2/3

Cara langsung untuk mengetahui jika dua atau lebih pecahan bersamaan, adalah untuk menyatakan pecahan secara langsung dengan cara perpuluhan, dan jika semua digit bertepatan, pasti pecahannya bersamaan. Tetapi ada kaedah lain yang berkenaan dengan 2/3:

Kaedah 1

Menjadi pecahan x/y yang anda ingin tahu sama ada pecahan ini bersamaan dengan 2/3:

Tanda soal siasat diletakkan, kerana belum diketahui jika nilai "x" dan "y" memenuhi persamaan. Untuk mengetahui ia berlipat ganda di salib:

Boleh melayani anda: Hubungan perkadaran: konsep, contoh dan latihan

3x =? 2 dan

Hanya apabila kesamaan dipenuhi, terdapat kepastian bahawa x/y adalah pecahan bersamaan dengan 2/3.

Kaedah 2

Kaedah ini memerlukan menentukan pembahagi maksimum maksimum (MCD) pengangka dan penyebut. Maka kedua.

Contoh

Contoh 1

Tentukan sama ada pecahan 40/60 bersamaan dengan ⅔.

Penyelesaian

Oleh kaedah 1:

Kaedah ini menunjukkan bahawa ia harus didarabkan di salib:

40 x 3 =? 60 x 2

120 =? 120

Oleh kerana kesamaan dipenuhi, disimpulkan bahawa 40/60 bersamaan dengan 2/3.

Contoh 2

Tentukan sama ada pecahan 120/180 bersamaan dengan ⅔.

Penyelesaian

Dalam contoh ini, kaedah 2 terpakai. Perkara pertama ialah menentukan penguraian dalam faktor utama 120:

120 = 2³ ⋅ 3 ⋅ 5

Dan penguraian dalam faktor penyebut adalah:

180 = 2² ⋅ 3² ⋅ 5

Untuk menentukan MCD, faktor umum didarab dengan eksponen yang lebih rendah:

MCD (120; 180) = 2² ⋅ 3 ⋅ 5 = 60

Jadi:

120 ÷ 60 = 2

180 ÷ 60 = 3

Oleh itu, disimpulkan bahawa 120/180 bersamaan dengan 2/3, iaitu:

Latihan yang diselesaikan

Latihan 1

Adalah pecahan 10/15 dan 12/18?

Penyelesaian

Cara terpantas untuk mengesahkannya adalah untuk membiak ke dalam salib, kerana mereka bukan nilai yang sangat besar:

10 x 18 =? 15 x 12

180 =? 180

Kesamaan diperoleh, maka dapat dikatakan bahawa 10/15 = 12/18.

Latihan 2

Adalah pecahan 8/12 dan 12/20 bersamaan dengan ⅔?

Penyelesaian

Kaedah penyederhanaan akan digunakan, yang terdiri daripada pembahagian secara serentak pengangka dan penyebut oleh faktor utama yang sama sehingga mencapai ungkapan yang tidak dapat dielakkan:

12/12 = 4/6 = ⅔, iaitu, pecahan pertama bersamaan dengan ⅔.

Untuk pecahan kedua yang anda ada:

12/20 = 6/10 = ⅗, tetapi ⅗ tidak dapat diatasi dan berbeza dari ⅔, oleh itu pecahan kedua tidak sama dengan ⅔.