Fungsi Injektif Apa yang terdiri daripada, apa itu dan contohnya

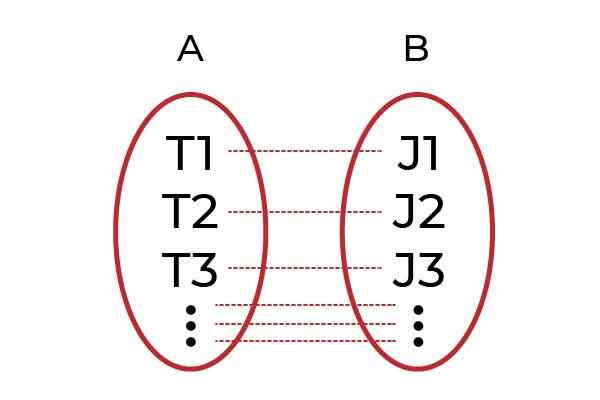
A Fungsi Injektif Ia adalah hubungan unsur domain dengan satu elemen codominium. Juga dikenali sebagai fungsi satu demi satu ( sebelas ), adalah sebahagian daripada klasifikasi fungsi mengenai cara di mana unsur -unsur mereka berkaitan.

Unsur codominium hanya boleh menjadi imej satu elemen domain, dengan cara ini nilai pemboleh ubah bergantung tidak dapat diulang.

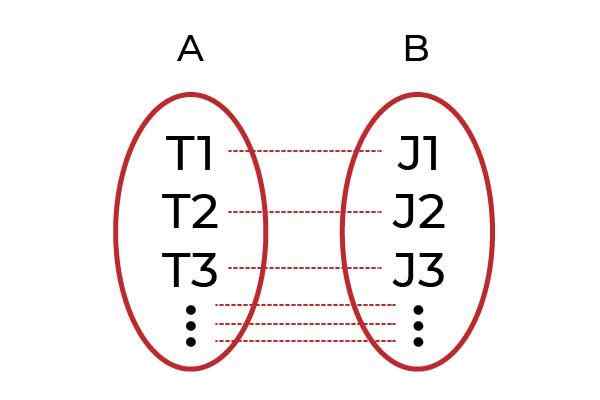
Sumber: Pengarang.

Contoh yang jelas adalah untuk mengumpulkan lelaki dengan kerja dalam kumpulan A, dan dalam kumpulan B kepada semua bos. Fungsinya F Ia akan menjadi yang mengaitkan setiap pekerja dengan bos mereka. Sekiranya setiap pekerja dikaitkan dengan bos yang berbeza melalui F, Jadi F  Ia akan menjadi satu Fungsi Injektif.

Untuk dipertimbangkan Injective Berikut ini mesti dipenuhi dengan fungsi:

∀ x₁  ≠ x₂   ⇒ f (x₁ ) ≠ f (x₂ )

Ini adalah cara algebra Untuk semua x₁ berbeza dari x₂ Anda mempunyai f (x₁ ) Berbeza dari f (x₂ ).

[TOC]

Apakah fungsi injaktif untuk?

Suntikan adalah harta fungsi berterusan, kerana mereka memastikan peruntukan imej untuk setiap elemen domain, aspek penting dalam kesinambungan fungsi.

Semasa melukis garis selari dengan paksi X Mengenai graf fungsi injektif, hanya graf yang harus disentuh pada satu titik, tanpa mengira ketinggian atau magnitud Dan Garisnya ditarik. Ini adalah cara grafik untuk membuktikan suntikan fungsi.

Cara lain untuk menguji jika fungsi adalah Injective, membersihkan pemboleh ubah bebas X Dari segi pemboleh ubah bergantung Dan. Maka ia harus disahkan jika domain ungkapan baru ini mengandungi nombor sebenar, pada masa yang sama bagi setiap nilai Dan Terdapat satu nilai dari X.

Fungsi pesanan atau hubungan mematuhi, antara bentuk lain, notasi F: d_F→C_F

Yang dibaca F yang pergi dari D_F ke c_F

Di mana fungsi F Kaitkan set Domain dan Codominium. Juga dikenali sebagai set permulaan dan set ketibaan.

Boleh melayani anda: pensampelan rawak: metodologi, kelebihan, kekurangan, contoh

Dominion D_F  Mengandungi nilai yang dibenarkan untuk pemboleh ubah bebas. Codominium C_F  Ia dibentuk oleh semua nilai yang ada kepada pemboleh ubah bergantung. Unsur -unsur C_F berkaitan dengan D_F  Mereka tahu bagaimana Julat fungsi (r_F ).

Penyaman fungsi

Kadang -kadang fungsi yang tidak injektif, dapat menjalani pengkondisian tertentu. Keadaan baru ini dapat mengubahnya menjadi a Fungsi Injektif. Semua jenis pengubahsuaian ke domain dan codominium fungsi adalah sah, di mana objektifnya adalah untuk memenuhi sifat suntikan dalam hubungan yang sepadan.

Contoh fungsi injektif dengan latihan yang diselesaikan

Contoh 1

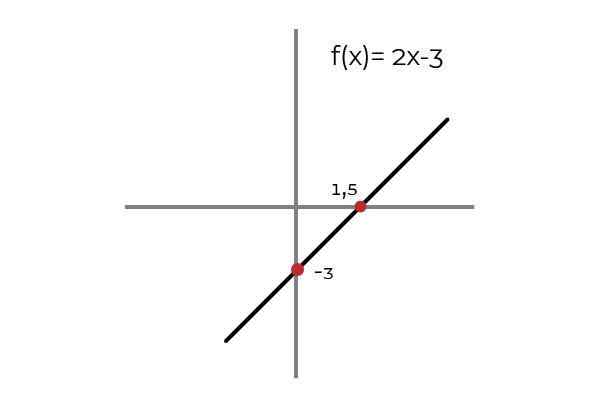
Menjadi fungsi F: r → R ditakrifkan oleh garis F (x) = 2x - 3

A: [Semua nombor sebenar]

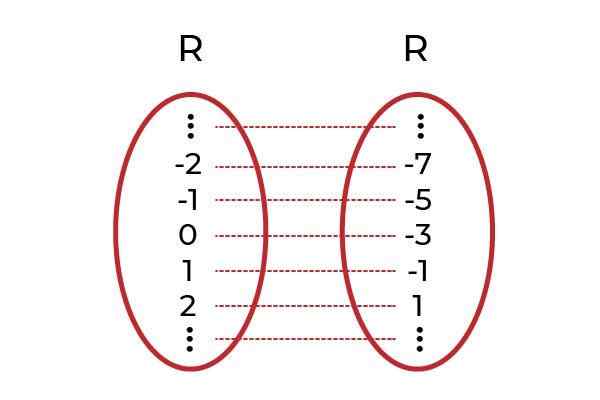
Sumber: Pengarang.

Diperhatikan bahawa untuk sebarang nilai domain terdapat imej dalam codominium. Imej ini unik, yang menjadikan f fungsi injektif. Ini terpakai kepada semua fungsi linear (fungsi yang tahap pembolehubah yang lebih besar adalah satu).

Sumber: Pengarang.

Contoh 2

Menjadi fungsi F: r → R ditakrifkan oleh F (x) = x² +1

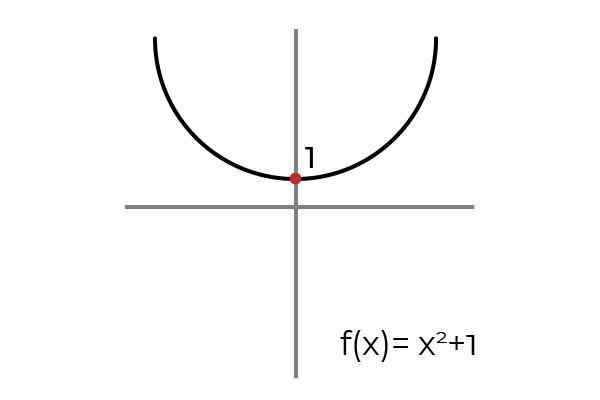Sumber: Pengarang

Semasa melukis garis mendatar, diperhatikan bahawa grafik dijumpai pada lebih dari satu kali. Kerana ini fungsi F tidak injektif semasa ditakrifkan  R → R

Domain fungsi dikondisikan:

                                               F: r⁺ Atau 0 → R

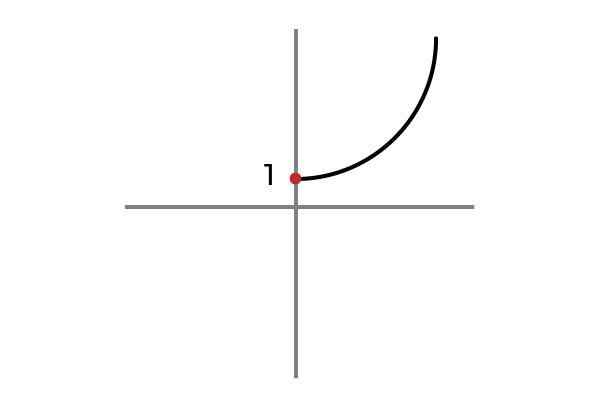Sumber: Pengarang

Sekarang pemboleh ubah bebas tidak mengambil nilai negatif, dengan cara ini ia dielakkan untuk mengulangi hasil dan fungsi F: r⁺ Atau 0 → R ditakrifkan oleh F (x) = x² + 1 adalah invective.

Satu lagi penyelesaian homolog adalah untuk mengehadkan domain ke kiri, iaitu, menyekat fungsi untuk hanya mengambil nilai negatif dan sifar.

Domain fungsi dikondisikan

                                               F: r^- Atau 0 → R

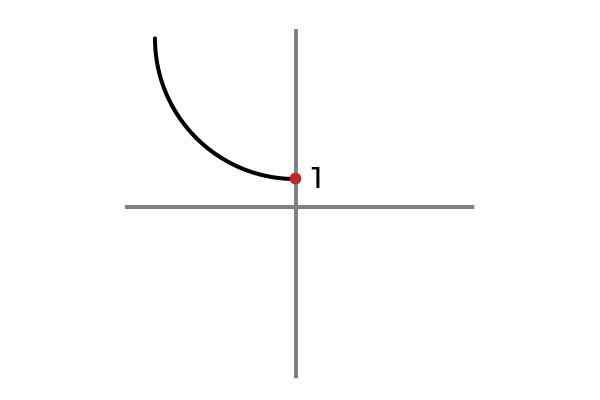Sumber: Pengarang

Sekarang pemboleh ubah bebas tidak mengambil nilai negatif, dengan cara ini ia dielakkan untuk mengulangi hasil dan fungsi F: r^- Atau 0 → R ditakrifkan oleh F (x) = x² + 1 adalah invective.

Fungsi trigonometri mempunyai tingkah laku yang serupa dengan gelombang, di mana ia sangat biasa untuk mencari pengulangan nilai dalam pemboleh ubah bergantung. Melalui pengkondisian tertentu, berdasarkan pengetahuan terdahulu mengenai fungsi -fungsi ini, kita dapat mengehadkan domain untuk memenuhi syarat -syarat suntikan.

Boleh melayani anda: mata coplanares: persamaan, contoh dan latihan yang diselesaikan

Contoh 3

Menjadi fungsi F: [ -π/2, π/2 ] → R ditakrifkan oleh F (x) = cos (x)

Dalam selang waktu [ -π/2 → π/2 ] Fungsi kosinus berbeza antara sifar dan satu.

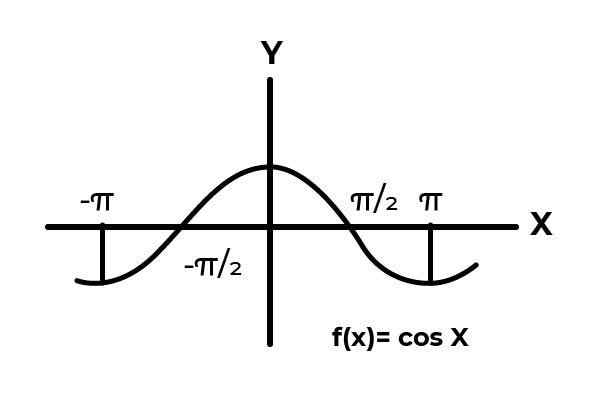Sumber: Pengarang.

Seperti yang dapat dilihat dalam grafik. Bermula dari awal x = -π/2 kemudian mencapai maksimum sifar. Ia adalah selepas x = 0 bahawa nilai -nilai mula diulang, sehingga kembali ke sifar x = π/2. Dengan cara ini diketahui bahawa F (x) = cos (x) tidak injak Untuk selang waktu [ -π/2, π/2 ] .

Semasa mengkaji grafik fungsi F (x) = cos (x) selang diperhatikan di mana tingkah laku lengkung menyesuaikan diri dengan kriteria suntikan. Seperti selang waktu

[0 , π ]

Di mana fungsi berbeza dari 1 hingga -1, tanpa mengulangi sebarang nilai dalam pemboleh ubah bergantung.

Dengan cara ini fungsi fungsi F: [0 , π ] → R ditakrifkan oleh F (x) = cos (x). Ia adalah invective

Terdapat fungsi bukan linear di mana kes -kes yang serupa dibentangkan. Untuk ungkapan rasional, di mana penyebut menempatkan sekurang -kurangnya satu pemboleh ubah, terdapat sekatan yang menghalang suntikan hubungan.

Contoh 4

Menjadi fungsi F: r → R ditakrifkan oleh F (x) = 10/x

Fungsi ini ditakrifkan untuk semua nombor sebenar kecuali 0 yang membentangkan ketidaktentuan (ia tidak dapat dibahagikan antara sifar).

Apabila menghampiri sifar di sebelah kiri pemboleh ubah bergantung mengambil nilai negatif yang sangat besar, dan sejurus selepas sifar, nilai pemboleh ubah bergantung mengambil angka positif yang besar.

Gangguan ini menjadikan ekspresi F: r → R ditakrifkan oleh F (x) = 10/x

Jangan injak.

Seperti yang dilihat dalam contoh -contoh sebelumnya, pengecualian nilai dalam domain berfungsi untuk "membaiki" ini. Zero dikecualikan dari domain, meninggalkan set set dan ketibaan yang ditakrifkan seperti berikut:

R - 0 → R

Di mana R - 0 melambangkan sebenar kecuali satu set yang satu -satunya elemennya adalah sifar.

Dengan cara ini ungkapan F: r - 0 → R ditakrifkan oleh F (x) = 10/x adalah injak.

 Contoh 5

Menjadi fungsi F: [0 , π ] → R ditakrifkan oleh F (x) = dosa (x)

Dalam selang waktu [0 , π ] Fungsi sinus berbeza antara sifar dan satu.

Boleh melayani anda: pemboleh ubah rawak: konsep, jenis, contoh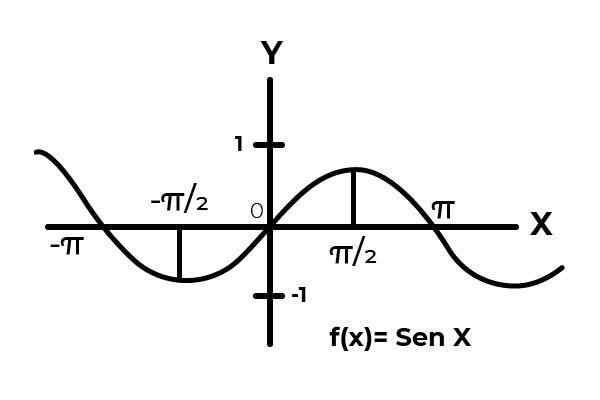Sumber: Pengarang.

Seperti yang dapat dilihat dalam grafik. Bermula dari awal x = 0 kemudian mencapai maksimum di x = π/2. Ia adalah selepas x = π/2 bahawa nilai mula diulang, sehingga kembali ke sifar x = π. Dengan cara ini diketahui bahawa F (x) = dosa (x) tidak injak Untuk selang waktu [0 , π ] .

Semasa mengkaji grafik fungsi F (x) = dosa (x) selang diperhatikan di mana tingkah laku lengkung menyesuaikan diri dengan kriteria suntikan. Seperti selang waktu  [  π/2,3π/2  ]

Di mana fungsi berbeza dari 1 hingga -1, tanpa mengulangi sebarang nilai dalam pemboleh ubah bergantung.

Dengan cara ini fungsi F: [  π/2,3π/2  ] → R ditakrifkan oleh F (x) = dosa (x). Ia adalah invective

Contoh 6

Sahkan jika fungsi F: [0, ∞) → R ditakrifkan oleh F (x) = 3x² Ia adalah invective.

Pada kesempatan ini domain ungkapan sudah terhad. Ia juga diperhatikan bahawa nilai pembolehubah bergantung tidak diulang dalam selang ini.

Oleh itu dapat disimpulkan bahawa F: [0, ∞) → R ditakrifkan oleh F (x) = 3x²   Ia adalah invective

Contoh 7

Kenal pasti fungsi berikut

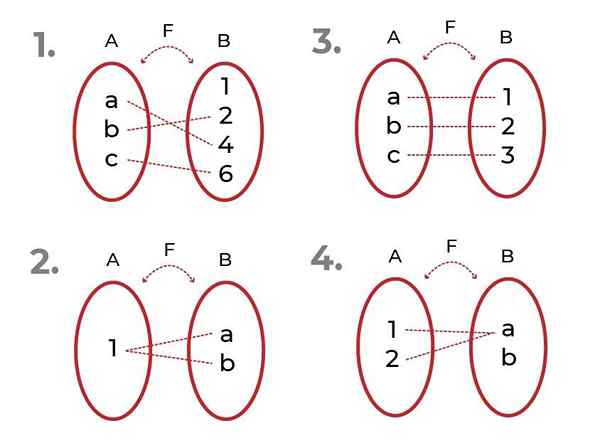Sumber: Pengarang

1. Ia adalah invective. Unsur -unsur yang berkaitan dengan codominium adalah unik untuk setiap nilai pemboleh ubah bebas.
2. Ia tidak injak. Terdapat unsur -unsur Co -oominium yang dikaitkan dengan lebih daripada satu elemen set permulaan.
3. Ia adalah invective
4. Ia tidak injak

Latihan yang dicadangkan untuk kelas/rumah

Sahkan sama ada fungsi berikut adalah injak:

F: [0, ∞) → R ditakrifkan oleh F (x) = (x + 3)²  

F: [ π/2,3π/2  ] → R ditakrifkan oleh F (x) = tan (x)

F: [ -π,π  ] → R ditakrifkan oleh F (x) = cos (x + 1)

F: r → R ditakrifkan oleh garis F (x) = 7x + 2

Rujukan

1. Pengenalan kepada logik dan pemikiran kritikal. Merrilee h. Salmon. Universiti Pittsburgh
2. Masalah dalam analisis matematik. Piotr Bilar, Alfred Witkowski. Universiti Wroclaw. Tiang.
3. Unsur analisis abstrak. Mícheál O'Searcoid PhD. Jabatan Matematik. Universiti Kolej Dublin, Beldfield, Dublind 4.
4. Pengenalan kepada Logik dan Metodologi Sains Deduktif. Alfred Tarski, New York Oxford. Oxford University Press.
5. Prinsip Analisis Matematik. Enrique Linés Escardó. Editorial reverté s. Hingga 1991. Barcelona, ​​Sepanyol.