Sifat fungsi logaritma, contoh, latihan

The fungsi logaritma Ini adalah hubungan matematik yang mengaitkan setiap nombor sebenar positif x Dengan logaritma anda dan di pangkalan ke. Hubungan ini memenuhi keperluan untuk menjadi fungsi: setiap elemen x milik domain mempunyai imej yang unik.

Oleh itu:

f (x) = y = log_ke x , Dengan> 0 dan berbeza dari 1.

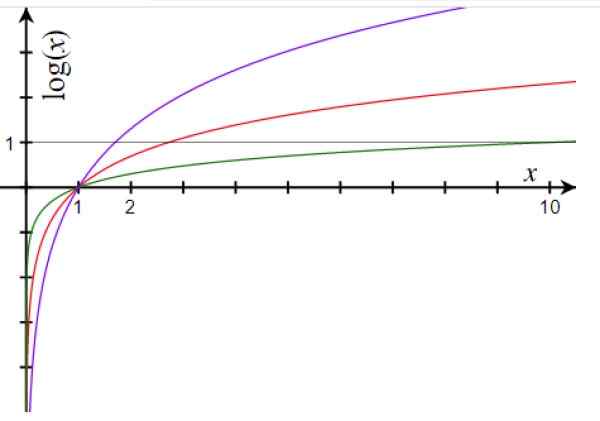
Rajah 1. Grafik fungsi logaritma untuk asas 10 (hijau), asas e (merah) dan asas 1.7 (ungu). Sumber: Wikimedia Commons.

Sifat utama fungsi logaritma adalah:

-Domainnya adalah semua reais lebih besar daripada 0, tidak termasuk 0. Dengan kata lain, tidak ada logaritma atau nombor negatif di mana -mana pangkalan. Dalam bentuk selang:

matahari _F = (0, ∞+)

-Logaritma nombor boleh menjadi negatif, positif atau 0, supaya julat atau laluannya adalah:

RGO _F = (--∞+)

-Fungsi logaritma sentiasa berkembang untuk> 1 dan menurun<1.

-Kebalikan dari f (x) = log_ke x Adakah fungsi eksponen.

Sesungguhnya fungsi logaritma berdasarkan, adalah fungsi songsang fungsi yang berpotensi:

F^-1(x) = a^dan

Sejak logaritma berasaskan ke nombor x, Itu nombornya dan yang mana asas mesti dibangkitkan ke untuk mendapatkan x.

-Logaritma asas selalu 1. Oleh itu, graf f (x) = log_ke x Sentiasa bersilang ke paksi x pada titik (1.0)

-Fungsi logaritma adalah transenden dan tidak dapat dinyatakan sebagai polinomial atau sebagai quotient ini. Sebagai tambahan kepada logaritma, kumpulan ini termasuk fungsi trigonometri dan eksponen, antara lain.

[TOC]

Contoh

Fungsi logaritma dapat ditubuhkan melalui pelbagai pangkalan, tetapi yang paling banyak digunakan adalah 10 dan dan, di mana dan Ia adalah bilangan euler yang sama dengan 2,71828 .. .

Apabila asas 10 digunakan, logaritma dipanggil logaritma perpuluhan, logaritma kasar, briggs atau hanya logaritma kering.

Dan jika nombor E digunakan, maka ia dipanggil Logaritma Neperian, oleh John Napier, ahli matematik Scotland yang menemui logaritma.

Boleh melayani anda: songsang berbilang: penjelasan, contoh, latihan yang diselesaikan

Notasi yang digunakan untuk masing -masing adalah seperti berikut:

-Logaritma perpuluhan: log₁₀ x = log x

-Logaritma Neperian: ln x

Apabila pangkalan lain akan digunakan, ia benar -benar perlu. Sebagai contoh, jika ia mengenai logaritma pada asas 2, ia ditulis:

y = log₂ x

Mari kita lihat nombor 10 logaritma dalam tiga pangkalan yang berbeza, untuk menggambarkan perkara ini:

Log 10 = 1

ln 10 = 2.30259

log₂ 10 = 3.32193

Kalkulator biasa hanya membawa logaritma perpuluhan (LOG) dan logaritma neperian (fungsi LN). Di internet terdapat kalkulator dengan pangkalan lain. Walau apa pun, pembaca dapat mengesahkan, dengan bantuan yang sama, dengan nilai sebelumnya ia dipenuhi:

10¹ = 10

dan^2.3026 = 10.0001

2^3.32193 = 10.0000

Perbezaan perpuluhan kecil disebabkan oleh jumlah perpuluhan yang diambil dalam pengiraan logaritma.

Kelebihan logaritma

Antara kelebihan menggunakan logaritma adalah kemudahan yang mereka berikan untuk bekerja dengan jumlah besar, menggunakan logaritma mereka dan bukannya nombor secara langsung.

Ini mungkin kerana fungsi logaritma tumbuh lebih perlahan kerana angka lebih besar, seperti yang kita hargai dalam grafik.

Oleh itu, dalam hal jumlah yang sangat besar, logaritma mereka jauh lebih kecil, dan memanipulasi bilangan kecil selalu lebih mudah.

Di samping itu logaritma memenuhi sifat berikut:

-Produk: log (a.b) = log a + log b

-Quotient: log (a/b) = log a - log b

-Kuasa: log a^b = b.log a

Dan dengan cara ini, produk dan kuota menjadi jumlah dan penolakan nombor yang lebih kecil, sementara potentiasi berubah menjadi produk mudah walaupun kuasa tinggi.

Itulah sebabnya logaritma membolehkan untuk menyatakan nombor yang berbeza -beza dalam julat nilai yang sangat besar, seperti intensiti bunyi, pH penyelesaian, kecerahan bintang, rintangan elektrik dan intensiti gempa bumi pada Richter skala.

Boleh melayani anda: Sudut alternatif luaran: Latihan dan Latihan DiselesaikanRajah 2. Logaritma digunakan pada skala Richter untuk mengukur magnitud gempa bumi. Imej itu menunjukkan bangunan runtuh di Concepción, Chile, semasa gempa bumi 2010. Sumber: Wikimedia Commons.

Mari kita lihat contoh pengendalian sifat -sifat logaritma:

Contoh

Cari nilai x dalam ungkapan berikut:

log (5x +1) = 1 + log (2x-1)

Jawapan

Kami mempunyai persamaan logaritma di sini, memandangkan hakikat bahawa yang tidak diketahui adalah pada hujah logaritma. Ia diselesaikan dengan meninggalkan satu logaritma pada setiap sisi persamaan.

Kami mulakan dengan meletakkan semua istilah yang mengandungi "x" di sebelah kiri kesamaan, dan yang mengandungi hanya nombor di sebelah kanan:

log (5x+1) - log (2x -1) = 1

Di sebelah kiri kita mempunyai penolakan dua logaritma, yang boleh ditulis sebagai logaritma kuota:

log [(5x+1)/ (2x-1)] = 1

Walau bagaimanapun, di sebelah kanan adalah nombor 1, yang dapat kita nyatakan sebagai log 10, seperti yang kita lihat sebelumnya. Jadi:

log [(5x+1)/ (2x-1)] = log 10

Untuk kesamaan dipenuhi, hujah logaritma mestilah sama:

(5x+1)/ (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Latihan Permohonan: Skala Richter

Pada tahun 1957 gempa bumi berlaku di Mexico yang magnitudnya adalah 7.7 pada skala Richter. Pada tahun 1960 satu lagi gempa magnitud yang paling banyak berlaku di Chile, 9.5.

Kirakan berapa kali gempa bumi Chile lebih sengit daripada Mexico, mengetahui bahawa magnitud m_R Pada skala Richter ia diberikan oleh formula:

M_R = log (10⁴ Yo)

Penyelesaian

Besarnya dalam skala Richter gempa bumi adalah fungsi logaritma. Kita akan mengira intensiti setiap gempa bumi, kerana kita mempunyai magnitud Richter. Mari Lakukan Langkah demi Langkah:

Boleh melayani anda: Nombor Primo: Ciri, Contoh, Latihan

-Mexico: 7.7 = log (10⁴ Yo)

Oleh kerana kebalikan dari fungsi logaritma adalah eksponen, kami memohon ini di kedua -dua belah persamaan dengan niat untuk membersihkan I, yang terdapat dalam hujah logaritma.

Oleh kerana mereka adalah logaritma perpuluhan, pangkalannya adalah 10. Jadi:

Dalam tempoh kanan, 10 dan log (10⁴ I) Mereka dibatalkan (seperti akar persegi dan persegi), yang: Meninggalkan:

10 ^7.7 = 10⁴ Yo

Keamatan gempa bumi Mexico adalah:

Yo_M = 10 ^7.7 / 10⁴ = 10^3.7

 -Cabai: 9.5 = log (10⁴ Yo)

Prosedur yang sama membawa kita ke intensiti gempa bumi Chile i_Ch:

Yo_Ch = 10 ^9.5 / 10⁴ = 10^5.5

 Sekarang kita dapat membandingkan kedua -dua intensiti:

Yo_Ch / Yo_M = 10^5.5 / 10^3.7 = 10^1.8 = 63.1

 Yo_Ch = 63.1. Yo_M

Gempa bumi Chile adalah kira -kira 63 kali lebih sengit daripada Mexico. Oleh kerana magnitud adalah logaritma, ia tumbuh lebih perlahan daripada intensiti, jadi perbezaan 1 dalam magnitud bermakna amplitud 10 kali lebih besar dari gelombang seismik.

Perbezaan antara magnitud kedua -dua gempa adalah 1.8, oleh itu kita dapat mengharapkan perbezaan intensiti lebih dekat dengan 100 daripada 10, seperti yang berlaku dengan berkesan.

Sebenarnya, jika perbezaannya adalah 2 tepat, gempa bumi Chile akan 100 kali lebih sengit daripada orang Mexico.

Rujukan

1. Carena, m. 2019. Manual Matematik PraUniversiti. Universiti Kebangsaan Pantai.
2. Figuera, j. 2000. Matematik 1st. Tahun yang pelbagai. Edisi bersama.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.
5. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.