Formula Undang-undang Biot-Savart, Demonstrasi, Aplikasi, Latihan

The Undang-undang Biot-Savart mewujudkan hubungan antara medan magnet dB  pada titik p, yang dihasilkan oleh dawai nipis yang mengangkut arus i dan panjang pembezaannya adalah ds. Undang -undang ini digunakan untuk mencari medan magnet pengagihan semasa melalui Prinsip Superposisi. 

Ini bermakna untuk mengira jumlah medan magnet pada titik p, kita mesti menambah semua sumbangan bahawa setiap bahagian pembezaan ds wayar menyumbang. Dan jumlah ini dilakukan melalui integral yang dijalankan sepanjang pengedaran semasa.

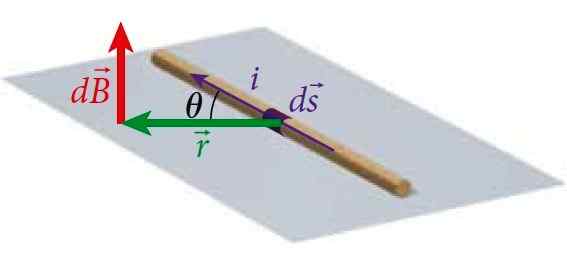
Rajah 1. Segmen wayar mengangkut arus semasa, yang menghasilkan medan magnet pada titik p pada jarak tertentu dari dawai, yang dikira oleh undang-undang biot-savart. Sumber: Bauer, W. Fizik untuk Kejuruteraan dan Sains.

Dengan cara ini, anda boleh mengira medan yang menghasilkan wayar dengan arus geometri yang berbeza.

Undang-undang Biot-Savart dinamakan sempena dua ahli fizik Perancis yang menemuinya pada tahun 1820: Jean Marie Biot (1774-1862) dan Felix Savart (1791-1841). Untuk mencapai matlamat ini, mereka terpaksa mengkaji intensiti dan bentuk medan magnet yang dihasilkan oleh banyak pengagihan semasa.

[TOC]

Formula

Ekspresi matematik Undang-undang Biot-Savart adalah seperti berikut:

Ia mengekalkan analogi dengan setarafnya untuk mengira medan elektrik: Undang -undang Coulomb, hanya medan magnet DB dalam p ialah tegak lurus ke pesawat di mana dawai terletak. Kita dapat melihatnya dalam Rajah 1.

Ekspresi sebelumnya juga boleh ditulis seperti berikut:

Dalam kedua -dua ungkapan, r Ia adalah vektor kedudukan, diarahkan dari elemen semasa IDs ke titik di mana anda ingin mengira bidang.

Boleh melayani anda: pemuliharaan momentum linear: prinsip, contoh, latihan.

Untuk bahagiannya, r Dengan aksen circumflejo ia adalah vektor kesatuan yang diarahkan ke arah dan arah yang sama, tetapi dengan modul sama dengan 1. Vektor r Ia diwakili seperti berikut:

Atas sebab ini, dengan menggantikan persamaan sebelumnya -yang mempunyai r r³ Dalam penyebut- ungkapan r segera dicapai² Dalam penyebut.

Sebagai tambahan kepada vektor yang disebutkan di atas, formula mengandungi μ tetap μ_{Sama ada}, Panggilan Kebolehtelapan vakum dan Nilai siapa:

μ_{Sama ada} = 4π x10^-7 T.m/ a.

Jika kita ingin mengira vektor medan magnet, adalah perlu untuk mengintegrasikan semua taburan semasa, yang mana kita memerlukan data mengenai geometrinya:

Produk vektor dan peraturan tangan kanan

Undang-undang Biot-Savart melibatkan produk vektor antara vektor IDs dan r. Hasil produk vektor antara dua vektor juga merupakan vektor.

Dalam hal ini modul produk vektor ids x r IS: (IDS) ⋅ r ⋅Senθ, di mana θ adalah sudut antara IDs dan r, Seperti yang ditunjukkan dalam Rajah 1.

Dengan cara ini magnitud medan dB Ia diberikan oleh:

Arah dan makna dapat ditentukan dengan peraturan tangan kanan, yang digambarkan dalam angka ini:

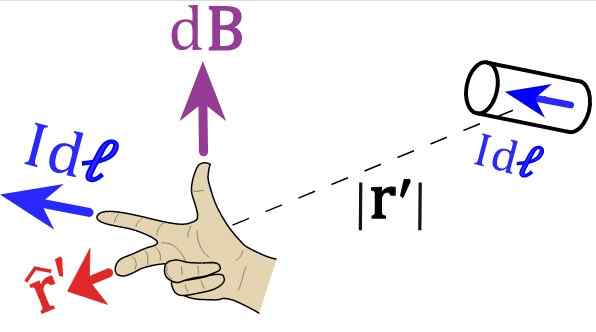Rajah 2. Peraturan Tangan Kanan untuk Undang-undang Biot-Savart. Sumber: Wikimedia Commons.

Kami menjemput pembaca untuk meletakkan tangan kanannya berikutan vektor angka 1 dan 2. Untuk Rajah 1, jari telunjuk mesti menunjuk ke kiri, mengikuti IDs atau idL, Jari tengah menunjuk mengikut vektor r kesatuan.

Dan akhirnya ibu jari diarahkan dan ini adalah arah medan magnet.

Boleh melayani anda: ellipsoid: ciri dan contoh

Demonstrasi Undang-undang Biot-Savart

Undang-undang Biot-Savart secara eksperimen, yang bermaksud bahawa perumusannya berasal dari banyak pemerhatian mengenai tingkah laku medan magnet yang dihasilkan oleh wayar semasa.

Pemerhatian Biot dan Savart

Ini adalah pemerhatian saintis Perancis mengenai medan magnet dB:

-Magnitud dB berkadar songsang dengan r².

-Ia juga berkadar terus dengan magnitud unsur semasa, yang dipanggil IDs Dan juga kepada sen θ, di mana θ adalah sudut antara vektor ds dan r.

-dB berserenjang dengan kedua -dua IDs -arah arus- r.

-Beragam dB adalah tangen ke lingkaran radio r wayar -centered. Dalam erti kata lain, bidang B yang dihasilkan oleh segmen semasa terdiri daripada lilitan sepusat ke tandus.

-Makna di mana ia berkisar B Ia diberikan oleh peraturan ibu jari yang betul: ibu jari kanan ditunjuk ke arah arus dan empat jari yang tersisa dilengkapi di sekitar dawai, berikutan peredaran medan.

Semua pemerhatian ini digabungkan dalam ungkapan matematik undang -undang yang digambarkan sebelumnya.

Permohonan Undang-undang Biot-Savart

Apabila pengedaran semasa mempunyai simetri yang tinggi, integral dapat diselesaikan dengan mudah, mari kita lihat beberapa kes:

Dawai rectilinear dan nipis

Kawat rectilinear panjang l mengangkut arus semasa, seperti yang muncul dalam angka itu.

Ia menggambarkan geometri yang diperlukan untuk pengiraan bidang. Ini berserenjang dengan lembaran kertas, keluar ke satah jika aliran semasa dari kiri ke kanan, dan masuk sebaliknya (periksa dengan peraturan tangan kanan).

Boleh melayani anda: Paramagnetisme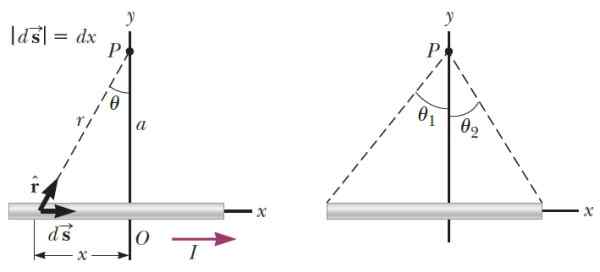Rajah 3.- Di sebelah kiri geometri yang diperlukan untuk mengira medan magnet yang menghasilkan segmen dawai nipis pada titik p. Di sebelah kanan sudut yang menentukan kedudukan p berkenaan dengan hujung segmen. Sumber: Serway, r. Fizik untuk Sains dan Kejuruteraan.

Menjadi k  Vektor unit ke arah yang berserenjang dengan satah, selepas menjalankan proses mengintegrasikan, medan magnet yang dihasilkan wayar dalam p adalah:

SPIRA Pekeliling

Gelung bulat radio ke Ia mengangkut arus seperti yang ditunjukkan dalam angka dan menghasilkan medan magnet dB -dalam warna hijau gelap p pada paksi paksi, dari jauh x dari pusat.

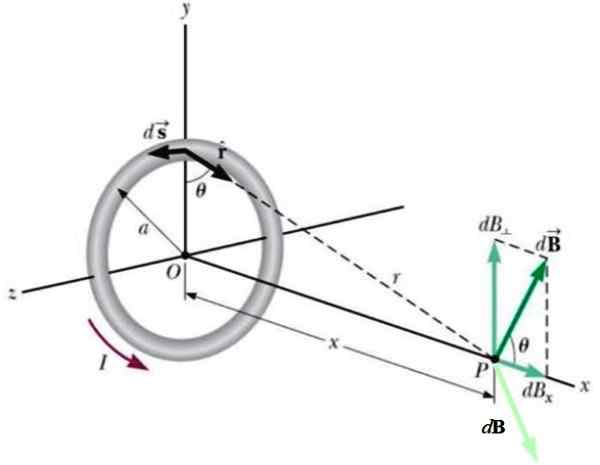Rajah 4.- Geometri untuk pengiraan medan yang dihasilkan oleh spase bulat pada titik p pada paksi paksi. Sumber: Wikimedia Commons.

Satu lagi elemen semasa yang terletak di seberang akan menghasilkan sumbangan lain kepada DB (cahaya hijau), sehingga komponen menegak dibatalkan dengan yang pertama.

Hasilnya adalah bahawa medan magnet bersih adalah mendatar, jadi ia hanya diintegrasikan ke dalam komponen ini, menghasilkan:

Latihan diselesaikan

Terdapat dawai yang sangat panjang yang mengangkut arus 2 ke mengalir seperti yang ditunjukkan dalam gambar. Kirakan magnitud medan magnet pada jarak radial 5 cm dari wayar.

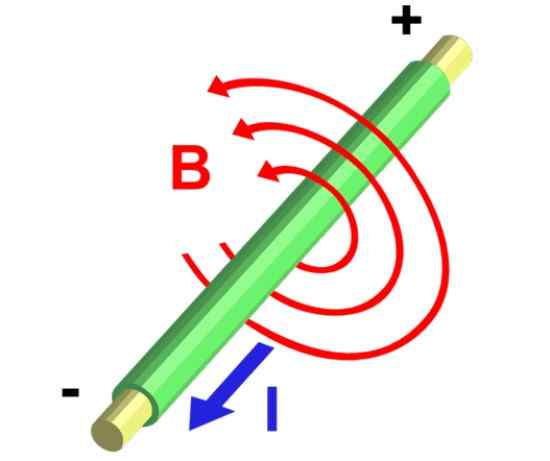Rajah 5.- Garis medan magnet segmen dawai rectilinear yang mengangkut arus. Sumber: Wikimedia Commons.

Penyelesaian

Oleh kerana ia adalah dawai yang sangat panjang, kita boleh mengambil ungkapan untuk segmen rectilinear dan membuat θ₁= 0º dan θ₂ = 180º untuk sudut had. Ini sudah cukup untuk panjang dawai untuk menyimpan tak terhingga.

Dengan cara ini kita akan mempunyai bidang ini:

Yang memudahkan:

Sekarang kita menggantikan nilai pernyataan:

I = 2 a

R = 5 x10^-2 m

μ_{Sama ada}= 4π x10^-7 T.m/ a

Arah dan rasa B Mereka ditunjukkan dalam Rajah 5, di mana arah yang meninggalkan lembaran telah diambil sebagai k.

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.
2. Figueroa, d. 2005. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
4. Resnick, r. 1999. Fizikal. Vol. 1. Edisi ke -3. dalam bahasa Sepanyol. Syarikat Editorial Continental s.Ke. daripada c.V.
5. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1.
6. Serway, r., Jewett, J. 2008. Fizik untuk Sains dan Kejuruteraan. Jilid 2. Ke -7. Ed. Pembelajaran Cengage.