Sifat nombor rasional, contoh dan operasi

The nombor rasional Mereka semua nombor yang boleh diperolehi sebagai pembahagian dua nombor keseluruhan. Contoh nombor rasional ialah: 3/4, 8/5, -16/3 dan yang muncul dalam angka berikut. Dalam nombor rasional yang ditunjukkan, mungkin untuk melakukannya kemudian jika diperlukan.

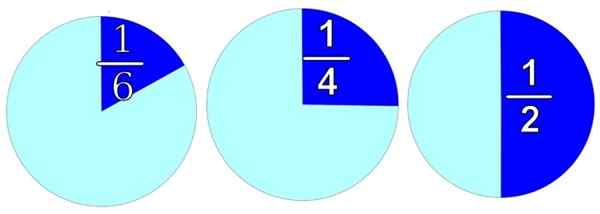
Dalam angka mana -mana objek diwakili, bulat untuk keselesaan. Sekiranya kita mahu membahagikannya kepada 2 bahagian yang sama, seperti di sebelah kanan, kita mempunyai dua bahagian dan masing -masing adalah 1/2.

Rajah 1. Nombor rasional digunakan untuk membahagikan keseluruhan ke pelbagai bahagian. Sumber: Freesvg.

Dengan membahagikannya kepada 4 bahagian yang sama, kita akan memperoleh 4 keping dan masing -masing bernilai 1/4, seperti dalam imej pusat. Dan jika anda perlu mengedarkannya dalam 6 bahagian yang sama, maka setiap bahagian akan bernilai 1/6, yang kita lihat dalam imej di sebelah kiri.

Sudah tentu, kita juga boleh membahagikannya kepada dua bahagian yang tidak sama, contohnya kita dapat menyimpan 3/4 bahagian dan menyimpan 1/4 bahagian. Bahagian lain juga mungkin, seperti 4/6 bahagian dan 2 bahagian. Yang penting ialah jumlah semua bahagian adalah 1.

Dengan cara ini, jelas bahawa dengan nombor rasional anda boleh membahagikan, mengira dan mengedarkan perkara seperti makanan, wang, tanah dan semua jenis objek dalam pecahan. Dan sebagainya jumlah operasi yang boleh dilakukan dengan nombor dilanjutkan.

Nombor rasional juga boleh dinyatakan secara decimally, seperti yang dapat dilihat dalam contoh berikut:

1/2 = 0.5

1/3 = 0.3333 ..

3/4 = 0.75

1/7 = 0.142857142857142857 ..

Kemudian kami menunjukkan bagaimana untuk lulus dari satu jalan ke jalan lain dengan contoh.

[TOC]

Sifat nombor rasional

Nombor rasional, yang set kami akan menandakan dengan huruf Q, mempunyai sifat berikut:

-Q Termasuk nombor semula jadi n dan keseluruhan nombor n.

Dengan mengambil kira bahawa mana -mana nombor ke Ia boleh dinyatakan sebagai kuota antara satu sama lain dan 1, mudah untuk melihat bahawa terdapat juga nombor semula jadi dan bilangan bulat.

Oleh itu, nombor semula jadi 3 boleh ditulis sebagai pecahan, dan juga -5:

3 = 3/1

-5 = -5/1 = 5/-1 = -(5/1)

Dengan cara ini ia adalah set berangka yang meliputi bilangan nombor yang lebih besar, sesuatu yang sangat diperlukan, meletakkan nombor "bulat" tidak mencukupi untuk menggambarkan semua operasi yang mungkin dilakukan.

Boleh melayani anda: 90 pembahagi: Apa dan penjelasan

-Nombor rasional boleh ditambah, dikurangkan, mengalikan dan membahagikan, hasil operasi menjadi nombor rasional: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.

-Antara setiap beberapa nombor rasional, nombor rasional yang lain selalu dapat dijumpai. Malah, di antara dua nombor rasional terdapat tak terhingga yang rasional. 

Sebagai contoh, antara rasional 1/4 dan 1/2 adalah rasional 3/10, 7/20, 2/5 (dan banyak lagi), yang boleh disahkan menyatakannya sebagai perpuluhan.

-Sebarang nombor rasional boleh dinyatakan sebagai: i) integer atau ii) perpuluhan terhad (ketat) atau akhbar: 4/2 = 2; 1/4 = 0.25; 1/6 = 0.1666666 ..

-Nombor yang sama boleh diwakili oleh pecahan setara tak terhingga dan semuanya tergolong dalam q. Mari lihat kumpulan ini:

Semuanya mewakili perpuluhan 0.428571 ..

-Di antara semua pecahan setara yang mewakili nombor yang sama, pecahan yang tidak dapat dielakkan, yang paling mudah, adalah Wakil Canonical nombor itu. Wakil kanonik contoh sebelumnya ialah 3/7.

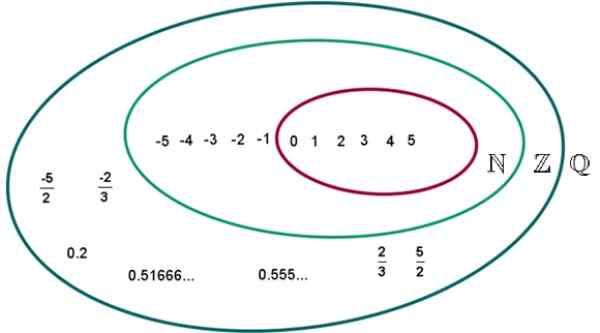Rajah 2.- Set q nombor rasional. Sumber: Wikimedia Commons. UVM Eduardo Artur/CC BY-S (https: // creativeCommons.Org/lesen/by-sa/4.0).

Contoh nombor rasional

-Pecahan sendiri, yang mana pengangka kurang daripada penyebut:

-Pecahan yang tidak betul, yang pengangka lebih besar daripada penyebut:

-Nombor semula jadi dan nombor keseluruhan:

-Pecahan setara:

Perwakilan perpuluhan nombor rasional

Apabila pengangka dibahagikan antara penyebut adalah bentuk perpuluhan nombor rasional. Sebagai contoh:

2/5 = 0.4

3/8 = 0.375

1/9 = 0.11111 ..

6/11 = 0.545454 ..

Dalam dua contoh pertama, jumlah perpuluhan adalah terhad. Ini bermaksud bahawa apabila pembahagian dibuat, rehat diperoleh.

Sebaliknya, dalam dua yang akan datang, bilangan perpuluhan tidak terhingga dan itulah sebabnya titik -titik yang ditangguhkan diletakkan. Dalam kes yang terakhir terdapat corak dalam perpuluhan. Dalam kes pecahan 1/9 Rajah 1 diulangi selama -lamanya, manakala dalam 6/11 ia adalah 54.

Ia boleh melayani anda: kebarangkalian kekerapan: konsep, bagaimana ia dikira dan contohnya

Apabila ini berlaku dikatakan bahawa perpuluhan adalah akhbar dan dilambangkan oleh aksen circumflex seperti berikut:

Mengubah perpuluhan ke pecahan

Sekiranya ia adalah perpuluhan yang terhad, koma hanya dihapuskan dan penyebutnya menjadi unit yang diikuti oleh seberapa banyak sifar sebagai angka mempunyai perpuluhan. Contohnya, untuk mengubah perpuluhan 1.26 di pecahan ia ditulis seperti ini:

1.26 = 126/100

Maka pecahan yang dihasilkan dipermudahkan hingga maksimum:

126/100 = 63/50

Sekiranya perpuluhan tidak terhad terlebih dahulu tempoh dikenalpasti. Kemudian langkah -langkah ini diikuti untuk mencari pecahan yang dihasilkan:

-Pengangka adalah penolakan antara bilangan (tiada koma atau aksen circumflex) dan bahagian yang tidak membawa aksen circumflex.

-Penyebut adalah integer dengan sebanyak 9 sebagai angka di bawah circumflex, dan seberapa banyak atau sebagai angka di bahagian perpuluhan mereka tidak berada di bawah circumflex.

Mari ikuti prosedur ini untuk mengubah nombor perpuluhan 0.428428428 ... di pecahan.

-Pertama tempoh dikenalpasti, iaitu urutan yang diulang: 428.

-Kemudian operasi menolak nombor tanpa koma atau aksen dilakukan: 0428 bahagian yang tidak mempunyai circumflex, iaitu 0. Ini adalah 428 - 0 = 428.

-Penyebut dibina, mengetahui bahawa di bawah circumflex terdapat 3 angka dan semuanya berada di bawah circumflex. Oleh itu penyebutnya adalah 999.

-Akhirnya pecahan terbentuk dan dipermudahkan jika boleh:

0.428 = 428/999

Tidak mungkin untuk mempermudah lebih banyak.

Operasi nombor rasional

- Tambah dan tolak

Pecahan dengan penyebut yang sama

Apabila pecahan mempunyai penyebut yang sama, tambahkannya dan/atau tolak mereka sangat mudah, kerana pengangka hanya ditambahkan secara algebra, meninggalkan sebagai penyebut hasil yang sama dengan penambahan yang sama. Akhirnya, jika boleh, ia dipermudahkan.

Contoh

Menjalankan jumlah algebra berikut dan memudahkan hasilnya:

Pecahan yang dihasilkan sudah tidak dapat dielakkan.

Pecahan dengan penyebut yang berbeza

Dalam kes ini, penambah digantikan dengan pecahan setara dengan penyebut yang sama dan kemudian prosedur sudah diterangkan. 

Contoh

Secara algebra menambah nombor rasional berikut memudahkan hasilnya:

Boleh melayani anda: tepi kubus

Langkah -langkahnya adalah:

-Tentukan Minimum Biasa (MCM) penyebut 5, 8 dan 3:

MCM (5,8,3) = 120

Ini akan menjadi penyebut pecahan yang terhasil tanpa memudahkan.

-Untuk setiap pecahan: Bahagikan MCM antara penyebut dan kalikan oleh pengangka. Hasil operasi ini diletakkan, dengan tanda masing -masing, dalam pengangka pecahan. Dengan cara ini pecahan bersamaan dengan asal diperolehi, tetapi dengan MCM sebagai penyebut.

Sebagai contoh, untuk pecahan pertama, pengangka dibina seperti ini: (120/5) x 4 = 96 dan diperoleh:

Teruskan dengan cara yang sama untuk pecahan yang tinggal:

Akhirnya, pecahan setara digantikan tanpa melupakan tanda mereka dan jumlah algebra dari pengangka dibuat:

(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =

= (96+210-440+24) / 120 = -110 / 120 = -11/12

- Pendaraban dan pembahagian

Pendaraban dan pembahagian dilakukan mengikut peraturan yang ditunjukkan di bawah:

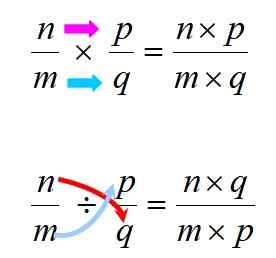Rajah 3. Peraturan untuk menjalankan pendaraban dan pembahagian nombor rasional. Sumber: f. Zapata.

Dalam apa jua keadaan, penting untuk diingat bahawa pendaraban adalah komutatif, yang bermaksud bahawa urutan faktor tidak mengubah produk. Ini tidak berlaku dengan bahagian ini, jadi anda mesti berhati -hati untuk menghormati perintah antara dividen dan pembahagi.

Contoh 1

Menjalankan operasi berikut dan memudahkan hasilnya:

a) (5/3) x (8/15)

b) (-4/5) ÷ (2/9)

Jawapan kepada

(5/3) x (8/15) = (5 x 8)/(3 x 15) = 15/120 = 1/8

Jawab b

(-4/5) ÷ (2/9) = (-4 x 9)/(5 x 2) = -36/10 = -18/5

Contoh 2     

Luisa mempunyai $ 45. Dia menghabiskan sepersepuluh membeli buku dan 2/5 bahagian dari apa yang tersisa dalam baju. Berapa banyak wang yang telah ditinggalkan oleh Luisa? Menyatakan hasilnya dalam pecahan yang tidak dapat dielakkan.

Penyelesaian

Kos Buku (1/10) x 45 $ = 0.1 x 45 $ = 4.5 $

Oleh itu Luisa tinggal bersama:

45 - 4.5 $ = 40.5 $

Dengan wang itu Luisa pergi ke kedai pakaian dan membeli baju itu, yang harganya:

(2/5) x 40.5 $ = 16.2 $

Sekarang Luisa ada dalam portfolio:

40.5 - 16.2 $ = 24.3 $

Untuk menyatakannya dalam pecahan, ia ditulis seperti ini:

24.3 = 243/10

Itu tidak dapat dielakkan.

Rujukan

1. Baldor, a. 1986. Aritmetik. Edisi dan Pengagihan Edisi Codex.
2. Carena, m. 2019. Manual Matematik. Universiti Kebangsaan Pantai.
3. Figuera, j. 2000. Matematik 8. Edisi bersama.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Nombor rasional. Pulih dari: cimanet.UOC.Edu.
6. Nombor rasional. Diperolehi dari: WebDelProfesor.Ula.Pergi.